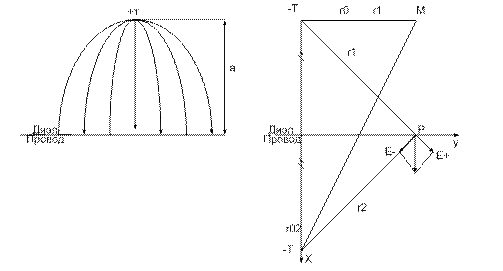
Часто требуется рассчитать поле зарядов расположенных вблизи пов-ти раздела правильной формы 2-х или нескольких сред. Сложность таких расчетов состоит в том, чтобы на поверхностях раздела появляются наведенные заряды, закон распределения которых заранее не известен в этом случае используется метод зеркальных изображений, согласно которому исходная сложная задача по расчету поля в нескольких средах сводится к эквивалентной простой задаче расчета поля в однородной среде. Поскольку при замене сред исчезает наведенные заряды, то их действия учитываются введением фиктивных зарядов. Величина знака и расположение фиктивных зарядов определяет из граничных условий исходной задачи.
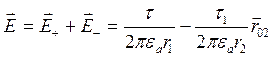 .
.
Определим напряженность и потенциал поля в диэлектрике.
Найдем величину (![]() ) такую, чтобы тангенциальная составляющая напряженности
поля на границе раздела (оси у) была бы равна 0.
) такую, чтобы тангенциальная составляющая напряженности
поля на границе раздела (оси у) была бы равна 0.
Напряженность точки Р
принадлежащей оси у. Т.к. ![]() то
для выполнения условия
то
для выполнения условия ![]() необходимо
обеспечить
необходимо
обеспечить ![]() .
.
В итоге можем определить напряженность поля в любой точке М.
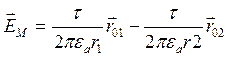 ;
; 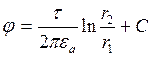 .
.
Формулы Максвелла для определения потенциалов,
зарядов и емкостей в системе проводников.
В ряде случаев необходимо рассчитать поле создаваемое системой заряженных тел расположенных над проводящей пов-ю. Вэтом случае используют 3 группы формул Максвелла, основанных на принципе наложения и метода зеркальных изображений. Определения отдельных составляющих этих формул для тел произвольной формы является сложной задачей. Практическое значение имеют формулы приблизительно к многопроводным линиям.
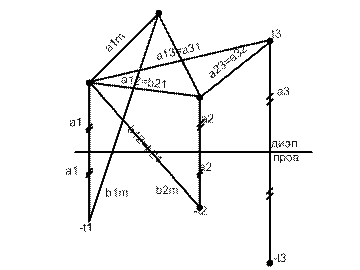 Пусть над проводящей
пов-ю расположено n проводов
Пусть над проводящей
пов-ю расположено n проводов ![]() -радиус
n-го повода
-радиус
n-го повода ![]() -высота
подвеса. Пусть
-высота
подвеса. Пусть ![]() ,
тогда фиктивная заряженная ось совпадает с осью самого провода.
,
тогда фиктивная заряженная ось совпадает с осью самого провода.
Определим потенциал точки
М в диэлектрике согласно методу наложения ![]()
![]() -составл. потенциала от действия провода №1
и т.д.
-составл. потенциала от действия провода №1
и т.д.
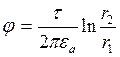 ;
; 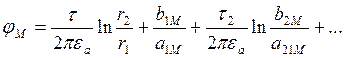
Перемесим точку М на
поверхность первого провода, тогда ![]() ;
; ![]() ;
; ![]() ;
; ![]() ; тогда потенциал 1 провода определим как
; тогда потенциал 1 провода определим как
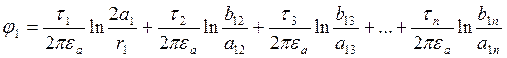 .
.
Аналогичное выражение можно записать для потенциалов остальных поводов в сокращенной форме записи:
![]()
![]() (*)
(*)
…………………………………...
![]()
-первая группа формул
Максвелла позволяет определить потенциалы проводов по известным зарядам. Здесь ![]() -потенциальные коэффициенты.
-потенциальные коэффициенты.
Они зависят от геометрических разрядов тел, их взаимного расположение и свойств среды.
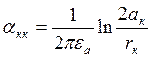 -собственный
потенциальный коэффициент, численно равен потенциалу к-того провода, если заряд
к-того провода равен 1, а заряды остальных проводов равны 0.
-собственный
потенциальный коэффициент, численно равен потенциалу к-того провода, если заряд
к-того провода равен 1, а заряды остальных проводов равны 0.
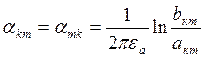 -
взаимный потенциальный коэфф., численно равен потенциалу
-
взаимный потенциальный коэфф., численно равен потенциалу ![]() к-того провода, если заряд n-го
провода
к-того провода, если заряд n-го
провода ![]() , а заряды остальных проводов равны 0.
, а заряды остальных проводов равны 0.
Все потенциальные коэффициенты – положительны.
Запишем 1 группу для сектора из 2 проводов.
![]()
![]()
Будем считать известными потенциалы проводов, а заряды подлежат определению:
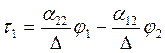 ,
где
,
где 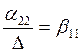
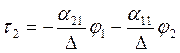 ,
где
,
где 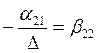
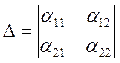
Обозначим:
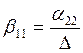 ;
; 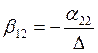 ;
; 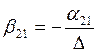 ;
; 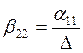 ;
; ![]() .
.
Коэффициент ![]() можно записать в др. виде:
можно записать в др. виде:
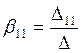 ;
; 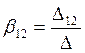 ;
; 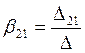 ;
; 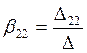 , где
, где ![]() .
.
Рассуждая аналогично, запишем вторую форму Максвелла для системы из 2 проводов.
![]() .
.
![]() (**)
(**)
…………………………
![]()
Где 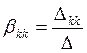 ;
;
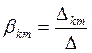 ;
; ![]() .
.
![]() -
собственный емкостный коэфф. численно равен заряду к-того провода при условии,
что потенциал к-того провода
-
собственный емкостный коэфф. численно равен заряду к-того провода при условии,
что потенциал к-того провода ![]() В, а потенциалы
ост.проводов = 0.
В, а потенциалы
ост.проводов = 0.
![]() -взаимный
емкостный коэфф. численно равен заряду к-того провода при условии, что
потенциал n-го провода = 3В, а потенциалы остальных проводов=0.
-взаимный
емкостный коэфф. численно равен заряду к-того провода при условии, что
потенциал n-го провода = 3В, а потенциалы остальных проводов=0.
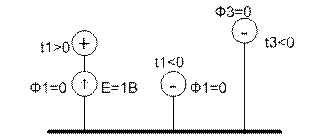
Запишем 2 группу формул Максвелла для системы 3-х проводов, изображенных на рисунке.
![]() .
.
![]()
…………
![]()
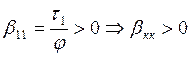 .
.
Все собственные емкостные коэфф.- положительны.
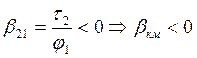 .
.
Последние обстоятельство является недостатком 2-й группы формул Максвелла.
Перепишем систему (**) так, чтобы в правой части были не потенциалы , а разности потенциалов между данным проводом и всем остальным в том числе и землей.
![]() т.к.
т.к. ![]()
![]() .
.
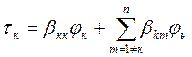
![]()
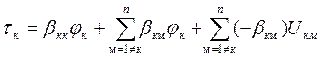
где 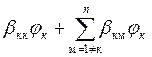 -полная сумма
-полная сумма
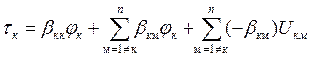
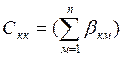 -собственная частичная емкость
-собственная частичная емкость
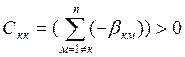 -взаимная частичная ёмкость.
-взаимная частичная ёмкость.
С учетом принятых обозначений:
![]() .
.
![]() (***)
(***)
…………………………
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.