Теория электромагнитного поля. Закон Кулона. Теорема Гаусса в интегральной форме, страница 10

Закон Ома в диффер-ой форме   устанавливает связь м/д вектором плотности тока  и напряженностью  в рассматриваемой точке.

    , где   удельная проводимость среды. Закон справедлив для участков (областей) не занятых источ-ми ЭДС.      

В областях занятых источ-ми ЭДС сущ—ет стороннее поле, которое создается и поддерживается силами не электрического происхождения (химическими, термоэлект—ми и т. д.) Под действием стороннего поля  в источнике непрерывно происходит разделение зарядов: положит—е перемещ—ся к + источнка, отрицательные к минусу. Эти разделившиеся заряды , как и внутри ист—ка, так и вне его создают свое поле, напряж—ть которого  как и напряж—ть Кулоновского поля направлена от положит—ых зарядов к отрицат-м.

При протекании постоянного тока в цепи одни элект-е заряды непрерывно сменяются другими такимиже как и в предыдущие моменты времени. Поэтому  картина поля (при макроскопич-м рассмотрении) повторяются в смежные моменты времени. Поле носит какбы статический характер—это послужило основанием того, что поле созданное впроводящей среде разделивш—ся зарядами называют Кулоновым полем, и напряж-ть  называют напряж—ю Кулонова поля.

 Внури источника ЭДС сторонее поля и Кулоново поле направлены навстечу друг другу. Велечина результирующего поля определяется как .

Поэтому закон Ома в дифферен—ой форме для областей занятых источ--ми

ЭДС записывается в веде       

Первый закон Киргофа в интегральной и дифферен—ой форме.

Выделим в проводнике с током некоторый обьем. Ток втекающий в этот обьем в единицу времени должен быть равен току, вытекающему из него, иначе в этом обьеме происходило бы накопление зарядов, что противоречит опыту. Математически это условие записыватся так  - первый закон Киргофа в интегральной форме.

Возмем предел 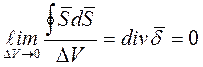 - первый закон Киргофа в дифферен-ой форме. Это соотношении означает, что линии вектора плотности тока не имеют не начала не конца, они замкнуты. Данное соотношение также называют законом непрерывности тока проводимости.

Лекция 12.

Закон Джоуля-Ленца в дифферен-ой форме.

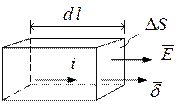
Рассмотрим некоторый обьем проводника с током. Мощность тепловых потер в этом обьёме                 = ,

отсюда мощность тепловых потерь рассматриваемая в единице обьема                  

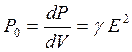          -- закон Д-Л в дифферен-ой форме. Справедлив для областей незанятых ситоч-ми ЭДС. Если рассматриваемый обьем содержит исьточ-ки ЭДС, то в этой области элект. поле постоянного тока не является потенциальныим  . И закон Джоуля-Ленца приобретает вид    .

Уравнение Лапласа для электрического поля в проводящей среде. 

В областях не занятых источ—ми ЭДС электрическое поле может рассматриваться как поле потенциальное, в котором напряжённость и потенцыал связаны соотношением: .

1^ый закон Киргофа в дифферен—ой форме :                                                                

для однородной и изотропной среды ,

.

Переход тока из среды с проводимостью в среду с провод—ю

Граничные условия.

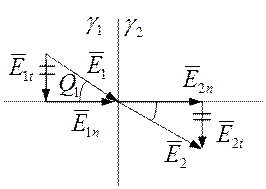                                      1. Е_1t=E_2t тангенцыальные сост—щие напряж—ти электр--го  поля одинаковы.Доказательство этого равенства аналогично. Доказ—во такого равенства дляэлектростат—го поля

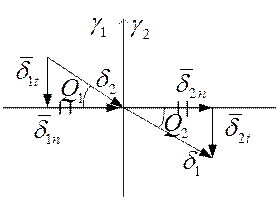
2.  нормальные составляющие векторов плотности тока равны.Доказ--во этого равенства идентично доказ—ву равенста  D_1n=D_2n

в электростатич—ом поле с заменой соотношения  в электростатике на  в поле постоянного тока. 

Следствие:     

Аналогия м/д элект—м полем постояннго тока в проводящей среде и электростатич –м полем.  

По своей природе эти поля различны. Элек.стаатич—ое поле создается неподвижными зарядоми; поле в проводящей среде—это поле в котором электр—е заряды движутся под воздействием внешнего источника. Сопоставим электрич—е поле в проводящей среде вне истч—ка ЭДС и электростатич—е поле в области, где не свободных зарядов.

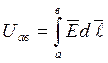
    D        E_1t =E_2t   D_1n =D_2n