Теория электромагнитного поля. Закон Кулона. Теорема Гаусса в интегральной форме, страница 6

  Сводится к определению 3-х скалярных функций соответствующих 3-м проекциям напряженности на 3 оси. Зачастую это сложная задача. Её можно упростить применением уравнения Пуассона (Лапласа). Значения этих ур-й для расчета поля в однородной среде заключается в том, что сложное решение, для вектора напр-ти , заменение уравнения в частных производных  для скалярной величины потенциала . Уравнение Пуассона (Лапласа) вытекает из теоремы Гаусса в дифф. Форме.

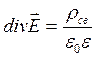, учтем, что  получаем

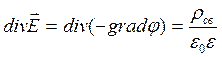
для однородной среды справедливо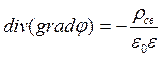

                                                    

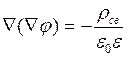
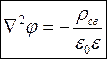                                                      - уравнение  Пуассона.

  В декартовой системе координат.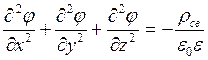      

  Уравнение Лапласа является частным случаем уравнения Пуассона когда . При интегр-ии ур-я  Пуассона (Лапласа) в решение входят постоянные интегрирования, которые определяются с помощью граничных условий.

Теорема единственности решения

Уравнение Пуассона (Лапласа) имеет  большое количество линейно независимых решений. Это отражает тот физический факт, что существует множество электростат. полей, потенциал каждого из которых удовлетворяет ур-ю Пуассона(Лапласа).

  Для того, чтобы выбрать решение необходимо воспользоваться теоремой единственности. Ф-я удовлетворяющая уравнению Пуассона (Лапласа) и граничных условием в данном поле, представляет собой искомое единственное решение задачи.

   Следствие.

1. Электростат. поле, ограниченное эквипотенциальным поверхностями и решение описывающие это поле не изменяется, если эти пов-ти рассматривать как пов-ти проводников которым сообщены одинаковые потенциалы.

                            

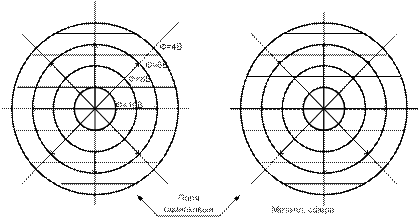
2. Электростат. поле на одну сторону от произвольной замкнутой поверхности S и решение описывающее это поле не изменяется если по другую сторону от этой пов-ти. Если измените параметры среды и распределение зарядов так, чтобы сохранить граничные условия на поверхности S.

   Данное следствие легло в основу метода зеркальных изображений.

Общая характеристика задач электростатики и методов их решения.

   Электростат. поле характер-ся одной из следующих величин .

   Основная задача электростатики (прямая задача) состоит в определении одной из этих величин как ф-ии координат (т.е. во всех точках поля). При этом должны быть заданы геометрии тех задающих поля и их заряды.

   Обратная задача состоит в опр-ии закона распред-и зарядов по заданному распределению напряженности или потенциалов полей. Для решения этой задачи часто используется уравнение Пуассона.

   Для решения прямой задачи применяют следующих: 1.Использование т. Гаусса в интегральной форме; 2.Применение метода наложения; 3.Непосредственное интегрирование уравнения Пуассона (Лапласа); 4.Метод зеркальных изображений; 5.Графмческий метод; 6.Матод моделирования и т.д.

Применение т. Гаусса.

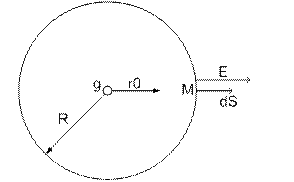  Дано:g, R, .

                                                  в точке М удаленной на расстояние R от заряда. Проведем ч/з точку М сферу так, чтобы все точки этой сферы оказались в одинаковых условиях по отношению к заряду. Тогда во всех точках этой сферы

а) ;   б) 

2-я форма записи т. Гаусса в интегральной форме записи.

           

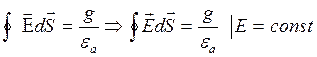
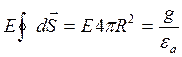
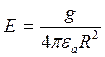
   В векторной форме: .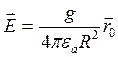

   Для определения потенциала как функции координат выберем такую систему координат, координатные поверхности которой совпадали бы с эквипотенциальными поверхностями рассматриваемой задачи. Очевидно, что в данном случае это сферическая система координат.

 

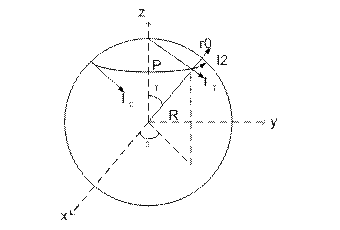
В этой системе, положение точки Р

характеризуется величинами -сферическими координатами точки Р.

 

В сферической системе координат градиент определяется как        .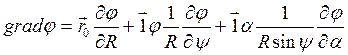

При изменении величины радиуса сферы (или изменении расстояния от точки Р до заряда) в выражении для градиента остается только одна составляющая).

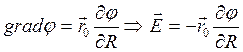
Тогда для модуле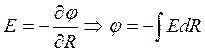й  или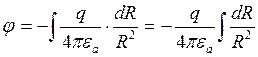

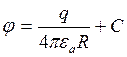
            Для определения величины постоянной интегрирования С принимаем равным нулю потенциал точки удаленной в => по отношению к заряду.

  при  

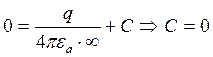
Пример: Определить напряженность и потенциал поля созданного заряженной осью на расстоянии r от оси.

Заряженная ось – тонкий теоретически бесконечно длинный проводник имеющий заряд на ед. длины равный .