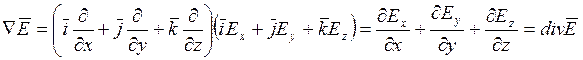
![]()
Отсюда следует ещё три формы записи теоремы Гаусса в дифференциальной форме:
![]()

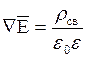
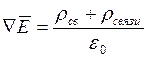
Поле внутри проводящего тела в условиях электростатики.
Поместим проводящее тело в электростатическое поле. Под действием поля в проводнике произойдёт перераспределение свободных зарядов: отрицательные заряды будут сосредоточены на поверхности, обращённые в сторону высокого потенциала внешнего поля, положительные заряды - обращённые в сторону низкого потенциала (явление электростатической индукции).
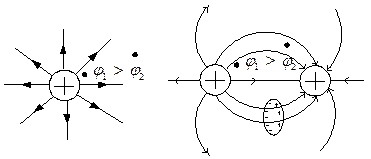
После завихрения перераспределения зарядов потенциалы всех точек будут одинаковыми (так как в противном случае заряды продолжат своё движение, что противоречит электростатике). Поэтому поверхность тела является эквипотенциальной и следовательно силовые линии внешнего поля подходят к ней под прямым углом.
Внутри тела ![]() так как внешнее поле
компенсируется полем зарядов располагающихся на поверхности проводника (так как
в противном случае заряды должны были бы двигаться).
так как внешнее поле
компенсируется полем зарядов располагающихся на поверхности проводника (так как
в противном случае заряды должны были бы двигаться).
Уравнение на границе раздела проводящего тела и диэлектрика.
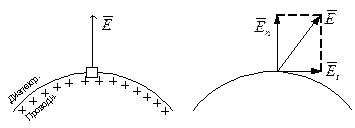
1)
Отсутствует тангенсальная составляющая
напряжённости поля: ![]()
2)
Модуль вектора электромагнитной
индукции в любой точке диэлектрика, непосредственно применяемый к поверхности
проводника, численно равен поверхностной плотности заряда ![]() на поверхности проводящего тела в этой
точке.
на поверхности проводящего тела в этой
точке.

Мысленно выделим бесконечно малый параллелепипед, верхняя грань которого, находится в диэлектрике, а нижняя в проводнике.
На основании теоремы Гаусса:
![]() , или
, или
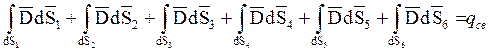
1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() =0, так как
=0, так как ![]() перпендикулярны.
перпендикулярны.
2) ![]() так как поле в
проводнике отсутствует, тогда
так как поле в
проводнике отсутствует, тогда
![]()
![]()
Граничные условия на поверхности раздела двух диэлектриков.
1. Тангенс состояния векторов напряжённости
электростатического поля равен ![]() .
.
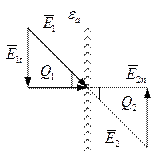
Выделим контур, охватывающий часть границы раздела такой, что
![]()
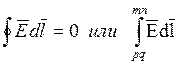
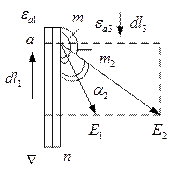
Пренебрегаем
свойствами интегрирования по сторонам ![]() :
:
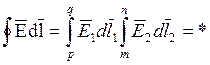
![]()
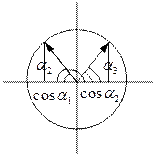
Считаем,
что в пределах стороны контура ![]() , векторы
, векторы ![]() ,
, ![]() .
.
![]() ;
;
где ![]()
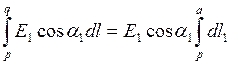 ,
,
![]() .
.
2) Нормальное составление векторов электрической индукции.
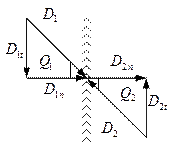

Выделим на границе раздела маленький сплошной параллелепипед и учтём, что внутри него нет свободных зарядов и есть только связанные.
В этом случае теорема Гаусса принимает вид:
![]()
![]()
Пренебрегаем соответствующими интегрированиями через малые боковые грани:
![]()
Считаем, что в пределах двух больших граней
параллелепипеда вектора ![]() ;
; ![]() , тогда:
, тогда:
![]()
где
![]() - площадь большой боковой грани.
- площадь большой боковой грани.
![]()
![]()
Ёмкость.
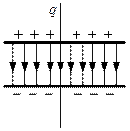

Пренебрегаем исканием поля у краёв конденсатора:
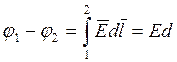
Заряд на одной плоскости, (пластине).
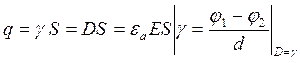 ,
, 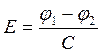
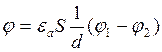
Для любой фиксированной в пространстве пары проводников отклонение заряда на одном из проводников к разности потенциалов между ними есть величина постоянная называется ёмкостью.
![]()
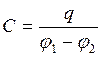
Для плоского контура без учёта: 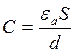
Ёмкость зависит от конфигурации тел, их размеров,
расстояние между телами и диэлектрических свойств диэлектрика ![]() .
.
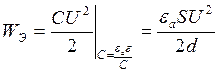
Определим объёмную плотность энергии электрического поля:

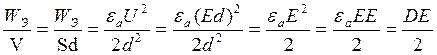
В общем случае (для неоднородного поля) объёмная плотность энергии вычисляется как:
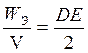
Две
пластины находятся в состоянии силового взаимодействия. Пусть под действием
силы ![]() пластинок с отрицательным зарядом
перемещается на расстояние
пластинок с отрицательным зарядом
перемещается на расстояние ![]() . Как изменится энергия
поля конденсатора в результате перемещения пластины?
. Как изменится энергия
поля конденсатора в результате перемещения пластины?
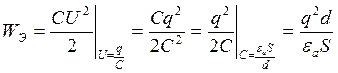
Отсюда следует, что уменьшение расстояния ![]() между пластинами при постоянстве заряда
между пластинами при постоянстве заряда ![]() на них приводит к перемещению энергии, то
есть работа силы по перемещению пластины производится за счёт убыли энергии
электрического поля.
на них приводит к перемещению энергии, то
есть работа силы по перемещению пластины производится за счёт убыли энергии
электрического поля.
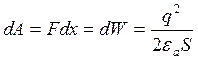
Определим величину силы приходящейся на единицу площади пластины.
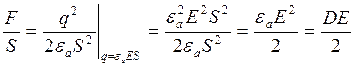
Получили аналогичное выражение.
Под ёмкостью уединенного тела понимают отношение
заряда на этом теле к его потенциалу, пологая, что второе тело удалено в ![]() и его
и его ![]() .
.
Определим ёмкость шара через ёмкость сферического конденсатора:
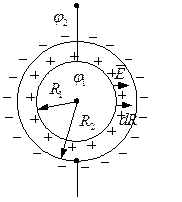
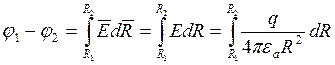
![]()
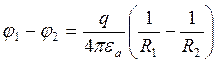
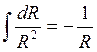
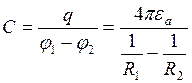 -ёмкость сферического конденсатора.
-ёмкость сферического конденсатора.
Для определения ёмкости шара необходимо положить ![]()
![]() .
.
Уравнение Пуассона. Уравнение Лапласа.
Непосредственное определение напряженности из уравнения;
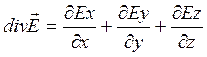
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.