Плоский контур стоком ![]() хар-ся векторной величиной –магнитным моментом
хар-ся векторной величиной –магнитным моментом
![]() Направление тока в контуре и направление
вектора магн-го момента связано с правилом буравчика. При неупорядоченном в
среднем движении электронов молекул в-ва их магнитные моменты взаимно уравновешиваются
.Если тело нах-ся во внешнем поле ,то происходит переориентация магн-х моментов
(намагничивания тела ),они приобретают в целом упорядоченную ориентированность,
создавая доп. Поле
Направление тока в контуре и направление
вектора магн-го момента связано с правилом буравчика. При неупорядоченном в
среднем движении электронов молекул в-ва их магнитные моменты взаимно уравновешиваются
.Если тело нах-ся во внешнем поле ,то происходит переориентация магн-х моментов
(намагничивания тела ),они приобретают в целом упорядоченную ориентированность,
создавая доп. Поле
![]()
 Мерой магн. сост.
в-ва служит вектор намагниченности
Мерой магн. сост.
в-ва служит вектор намагниченности ![]() равный среднему магн-му
моменту единицы объёма в-ва:
равный среднему магн-му
моменту единицы объёма в-ва:
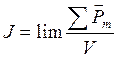 -этот
вектор определяет насколько магн-я индукция в данной среде
-этот
вектор определяет насколько магн-я индукция в данной среде![]() отличается от магн-й индукции в вакууме
при одной и той же потерях магн-го поля
отличается от магн-й индукции в вакууме
при одной и той же потерях магн-го поля ![]() В
однородных средах напряжённость и намагниченность пропорциональны
В
однородных средах напряжённость и намагниченность пропорциональны![]() - абсолютная магн-я восприимчивость в-ва.
- абсолютная магн-я восприимчивость в-ва.
Тогда: 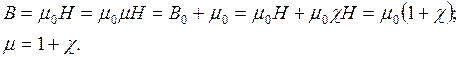
Магнитный поток ![]() через замкнутую пов-ть
через замкнутую пов-ть ![]()
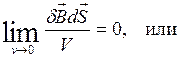
![]() - з-н Кирхгофа в интегральной форме
записи. Магнитные силовые линии замкнуты сами на себя.
- з-н Кирхгофа в интегральной форме
записи. Магнитные силовые линии замкнуты сами на себя.
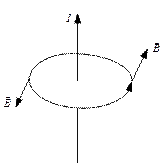
Закон полного тока в
интегр-й форме: Выделим в проводящей среде контур с ограниченной площадкой ![]()
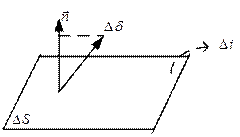 Определим
Определим ![]() -пронизывающего площадку
-пронизывающего площадку ![]() ,через величину величину плотности тока
,через величину величину плотности тока ![]() 0
0
![]() и
переходим к пределу
и
переходим к пределу 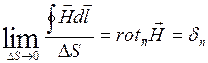
Если ориентировать площадку ![]() в пространстве так, что направление нормали
к ней совпадёт с направлением вектора плотности тока
в пространстве так, что направление нормали
к ней совпадёт с направлением вектора плотности тока ![]() ,то
вместо равенства проекций векторов можем записать равенство самих векторов :
,то
вместо равенства проекций векторов можем записать равенство самих векторов :![]()
![]() -закон полного тока
в дифференциальной форме для неизменных во времени полей (1-е ур-е Максвелла).
Физический смысл :Магнитное поле есть вихревое поле и линии вектора
-закон полного тока
в дифференциальной форме для неизменных во времени полей (1-е ур-е Максвелла).
Физический смысл :Магнитное поле есть вихревое поле и линии вектора ![]() являются замкнутыми .
являются замкнутыми .
 Первому ур-ю Максвелла можно
дать ещё одно физическое толкование: Вихревое магн-е поле возбуждается токами
проводимости. Скалярный потенциал магн-го поля :
Первому ур-ю Максвелла можно
дать ещё одно физическое толкование: Вихревое магн-е поле возбуждается токами
проводимости. Скалярный потенциал магн-го поля :
Если замкнутый контур
интегрирования не охватывает ток (говорят поле в области не занятой током ), то![]()
![]()
![]() магнитное поле в данной области можно рассматривать как поле потенциальное,
т.е. как поле каждая точка которого имеет скалярный магн-й потенциал
магнитное поле в данной области можно рассматривать как поле потенциальное,
т.е. как поле каждая точка которого имеет скалярный магн-й потенциал ![]() , тогда
, тогда ![]()
![]() или
или ![]()
![]()
Для однородной изотропной
среды ![]()
![]()
![]() или
или ![]()
![]()
·
![]()
![]()
Скалярный потенциал магн-го поля удовлетворяет ур-ю Лапласа.
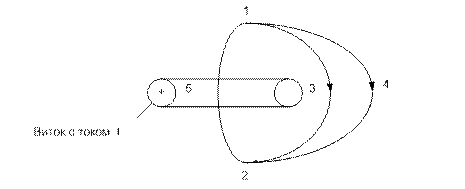
Разность скалярных магн-х потенциалов между точками 1 и 2 наз-т падением магн-го напряжения между точками 1 и 2
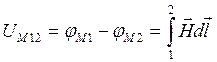
Падение магн-го напряж-я по выбранному пути (например 1 3 2) равно падению магн-го напряж-я по другому пути (1 4 2 ), если эти замкнутые пути образуют контур не охватывающий ток. В противном случае падения магн-го напряж-я будут отличаться на величину тока охватываемого контуром.
Контур 1 3 2 5 1
![]()
![]()
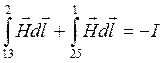
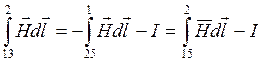
Граничные условия на пов-ти раздела 2-х сред с различными магнитными проницаемостями.
Пусть на пов-ти раздела отсутствует ток
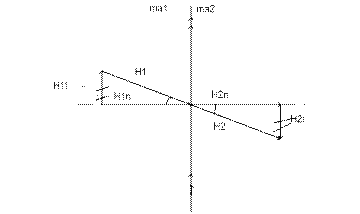
1.![]() (*).
(*).
Тангенциальные составляющие векторов напряжённости равны.
Доказательство равенства (*) аналогично доказательству выражения ![]() на границе раздела 2-х диэлектриков с
заменой соотношения.
на границе раздела 2-х диэлектриков с
заменой соотношения.
![]() в электростатическом поле на
в электростатическом поле на ![]() в магнитном поле.
в магнитном поле.
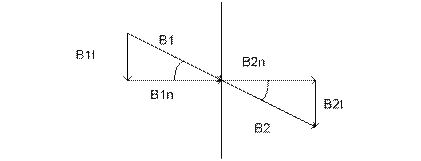
2.![]() (**).Нормальные составляющие векторов
магнитной инд-ции равны. Доказательство (**) аналогично доказательству
равенства
(**).Нормальные составляющие векторов
магнитной инд-ции равны. Доказательство (**) аналогично доказательству
равенства ![]() с заменой соотношения
с заменой соотношения ![]() на
на ![]() в
магн-м поле .
в
магн-м поле .
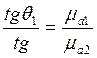
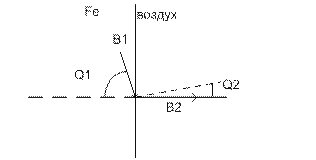
Отсюда
![]() что магн-е линии в воздухе подходят к
пов-ти тел из магнитомягких ферромагнитных матер-в под прямым углом.
что магн-е линии в воздухе подходят к
пов-ти тел из магнитомягких ферромагнитных матер-в под прямым углом.
Аналогия магн-го поля постоянного тока и электростатического поля.
Система ур-й магн-го поля для среды вне токов формально аналогична уравн-ям для электростат-го поля при отсутствии свободных зарядов.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Между картиной электростат-го поля и картиной магнитного поля может быть соответствие 2-х типов:
1-й тип – когда одинаково распределение линейных зарядов в электростат. поле и токов в линейных проводах .В этом случае картины полей одинаковы с той лишь разницей ,что силовые и эквипотенциальные линии меняются местами.
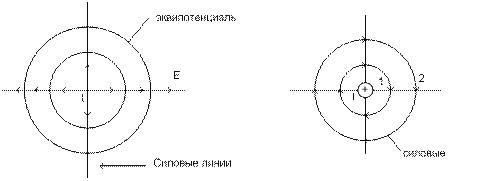
2-й тип соответствия – когда одинаковы формы граничных эквипотенциальных поверхностей в обоих полях. В этом случае картины полей совершенно одинаковы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.