Принцип действия и классификация турбинных ступеней., страница 9

При построении идеализированной схемы потока в ступени счита­ют, что окружная неравномерность его на входе в сопловой аппарат равна нулю, и сам поток является установившимся. Физически это до­пущение означает, что осевой зазор между рабочими лопатками преды­дущей ступени и соплами последующей достаточно велик и обеспечива­ет полное выравнивание потока за рабочими лопатками вплоть до ис­чезновения аэродинамических следов от них.

С точки зрения неравномерности потока по высоте каналов ис­пользуются различные идеальные схемы течения в зависимости от пос­тановки задачи.

Наиболее проста одномерная схема течения, в которой предполагается, что во входном сечении сопел поток равноме­рен не только по окружности, но и по их высоте. Далее от сечения 0-0 к сечениям 1-1 и 2-2 (см. рис.4) кинематические и динамические параметры потока меняются вдоль направления движения, оставаясь одинаковыми по площади каждого из названных сечений.

Несмотря на сравнительную простоту, одномерная трактовка ра­бочего процесса позволяет получить основные характеристики ступе­ни в целом. Она применима для определения параметров в контрольных сечениях и для расчета проходных площадей потока в них. Для внутриканального расчета одномерная теория ступени не пригодна. Приме­нительно к турбинной ступени, в которой, как правило, используются конфузорные каналы, полностью заполненные рабочей средой, послед­нее обстоятельство несущественно.

Для ступеней компрессора, в которых из-за положительного гра­диента давлений (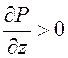) возможен отрыв и неполное заполнение межлопаточных каналов, использование одномерной теории более огра­ничено.

Кроме одномерной, используется  двумерная поста­новка решения задачи, при которой параметры и кинематику по­тока считают изменяющейся не только по ходу потока, но и по высоте каналов. В сочетании с предположением об окружной равномерности по­тока такая постановка задачи приводит к так называемой осесимметричной теории турбинной ступени.

В настоящее время прорабатывается трехмерная теория те­чения в ступени идеальной сжимаемой среды. Эта теория учитывает изменение параметров среды и в окружном направлении.

5. СИЛОВОЕ ВЗАИМОДЕЙСТВИЕ ПОТОКА И ОБЛОПАЧИВАНИЯ

5.1. Силы и моменты, действующие на лопаточный венец

Обозначим через ,  и  проекции на оси r, uи z равнодействующей сил, действующих на лопатку со стороны среды, про­текающей через произвольные соседние каналы лопаточного венца (рис.13). Если при полной степени впуска все каналы венца имеют одинаковые размеры и одинаковые условия протекания среды через них, то составляющие , ,  различных лопаток будут одинаковы по модулю и соответственно направлены. Равнодействующая сил , приложенных ко всем лопаткам венца, проходящая через ось вращения:

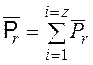                                                              .                                                    (12)

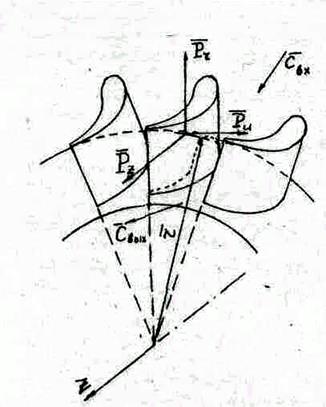
Рис.13. Разложение силы, действующей на лопатку на составляющие

Момент составляющих  относительно оси вращения:

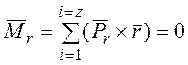                                                                                       .                                           (13)

Составляющие  всех каналов лопаточного венца образуют замкнутый многоугольник, поэтому их равнодействующая также равна нулю:

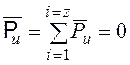                                                           .                                                (14)

Однако равнодействующий момент составляющих  относительно оси z, который является крутящим моментом, не равен нулю:

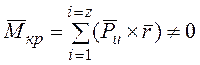                                                        .                                       (15)

В отличие от величины  в формуле (14) сумма модулей , называемая окружным усилием, не равна нулю:

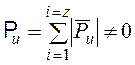                                                              .                                            (16)

Составляющие  параллельны и направлены в одну сторону - вдоль оси z, поэтому их равнодействующая не равна нулю:

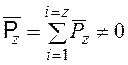                                                              .                                              (17)