Обычно касательные напряжения, связанные с молекулярной или микротурбулентной вязкостью на контрольных поверхностях, ограничивающих венец, не велики и не нарушают существенно справедливость турбинного уравнения. Однако при режимах резко отличающихся от расчетных в потоке появляются макротурбулентные пульсации, связанные с переносом КД и МКД из контрольной массы в смежные области за ее границами. Для учета этого обстоятельства следует вводить дополнительные члены в выражения крутящего момента и турбинного уравнения. Так, например, в случае центробежных машин показано, что рабочее колесо вызывает закрутку потока перед собой.
Ранее
постулировалось, что поток в контрольных сечениях является однородным. При
наличии неоднородности потока в окружном и радиальном направлениях используют
приведенное значение произведения 
во входном и выходном
контрольных сечениях:
,
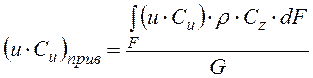(44)
где F - площадь контрольного сечения,
dF- элемент этой площади,
; 
; 
- значения соответствующих величин в
пределах элемента dF.
Если поток неравномерен только в радиальном направлении, то
,
и интеграл в числителе выражения (44) следует брать по радиусу. Такой прием используется при расчете длинных лопаток турбин.
Обязательным
условием использования выражения (44) являются наличие информации о полях
скоростей и плотности в пределах площади F. Эти поля
получены экспериментально лишь для отдельных частных случаев, что затрудняет
определение величины .
В
общем случае при неравномерных полях параметров во входном и выходном
контрольных сечениях движение в смежных решетках при рассмотрении его в
координатах, связанных с самими решетками, не является установившимся.
Учитывая, что периодичность потока в ступени - один оборот, приведенное
значение может быть найдено интегрированием на
протяжении одного оборота ротора.
С учетом периодичности движения уравнение Эйлера может дать в этом случае среднее значение мощности, а полученные ранее уравнения (34), (39) и (40) - средние значения момента и осевого усилия за один оборот.
Для ступени, которая не полностью уплотнена, применяется следующий прием: по уравнению Эйлера вычисляется мощность, которую может дать полностью уплотненная ступень, после чего дополнительно определяется и учитывается эффект наличия паразитных течений в неуплотненной ступени.
Отметим, что для отдельной осесимметричной струйки тока в турбинной ступени уравнение Эйлера применять нельзя. На ограничивающих ее поверхностях силовое воздействие потока происходит не только со стенками межлопаточного канала, но и с соседними струйками, поэтому и работа, определяемая упомянутым уравнением, может совершаться не только за счет передачи ее венцу, но и за счет энергообмена с соседними струйками.
8. ПОДОБИЕ И ХАРАКТЕРИСТИКИ РАБОЧЕГО ПРОЦЕССА
ТУРБИННЫХ СТУПЕНЕЙ
8.1. Подобие и числа подобия
Полное гидродинамическое подобие потоков имеет место, если соблюдаются геометрическое, кинематическое и динамическое подобие. В зависимости от характера течения (установившееся, неустановившееся) сил, действие которых необходимо учитывать (силы вязкости, гравитационные силы, упругие силы давления и т.д.), и свойств рабочего тела наличие подобия процессов, например, в турбинной ступени, определяется числами, или критериями подобия.
При наличии математической модели течения, исключающей нехарактерные факторы, она может являться базой для отыскания отмеченных чисел подобия. Точность выводов теории подобия, полученных на этой основе, определяется степенью близости математической модели к описываемому явлению. В ряде практически важных случаев исследуемые явления оказываются столь сложными, что описывающие их дифференциальные уравнения, невозможно решить или даже составить. Здесь на помощь приходит теория размерностей. В ней основные параметры, определяющие явления, считаются заданными, и предметом анализа является выявление комбинаций безразмерных независимых критериев подобия.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.