Примем за контрольную массу количество рабочей среды, заключенной в пределах венца облопачивания. Объем контрольной массы ограничен кольцевыми контрольными поверхностями ab и cd соответственно перед венцом и за ним, внутренними и наружными торцевыми поверхностями межлопаточных каналов и поверхностями самих лопаток. Поверхности ab и cd перпендикулярны к оси z (рис.14).
Сделаем следующие допущения:
- на контрольных поверхностях ab и cd окружные составляющие касательных напряжений равны нулю;
- венец считается полностью уплотненным, т.е. между контрольными сечениями протечек рабочей среды нет;
- степень
впуска ![]() ;
;
- в системе координат, связанной с венцом, поток является установившимся;
- течение в венце считается одномерным, среда - однородной в контрольных сечениях.
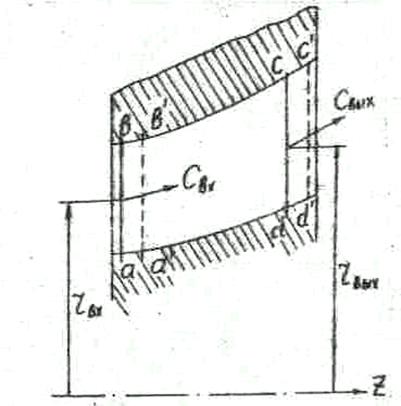
Рис.14. Схема лопаточного венца в меридиональной плоскости: ab, cd - следы кольцевых контрольных поверхностей
Используя
метод Лагранжа, проследим за изменением количества движения ![]() и момента количества движения
и момента количества движения ![]() контрольной массы за бесконечно малый
промежуток времени dt.
контрольной массы за бесконечно малый
промежуток времени dt.
За этот промежуток времени контрольная масса переместится вдоль по потоку. Соответственно контрольные поверхности ab и cd переместятся и займут положения a'b' и c'd'.
В
начальный момент времени t количество движения ![]() (abcd, t) контрольной
массы, заключенной в объеме между поверхностями ab и cd, можно
представить как сумму:
(abcd, t) контрольной
массы, заключенной в объеме между поверхностями ab и cd, можно
представить как сумму:
![]() . (19)
. (19)
Здесь в правой части записаны количества движения частей контрольной массы в объеме между поверхностями ab и b'а' и соответственно а'b' и cd . Аналогично момент количества движения для момента времени t:
![]() . (20)
. (20)
Подобным же образом для момента времени t + dt:
![]() , (21)
, (21)
![]() . (22)
. (22)
Изменение
количества движения рассматриваемой контрольной массы рабочего тела d(![]() ) находим как разность количеств движения в
моменты времени t и t + dt. Используя выражения (19) и (21), получим:
) находим как разность количеств движения в
моменты времени t и t + dt. Используя выражения (19) и (21), получим:
![]() . (23)
. (23)
В начальный момент времени t конечный момент t + dt в объеме a'b'cd будут содержаться различные частицы, но в связи со стационарностью движения все параметры во всех точках этого объема, равно как его масса и количество движения, в эти разные моменты времени будут одинаковыми. Поэтому
![]() .
.
В силу упомянутой стационарности движения оставшиеся члены в выражении (23) не будут зависеть от времени.
Учитывая сказанное, можно записать:
![]() . (24)
. (24)
Аналогично
определится и изменение ![]() за промежуток времени dt:
за промежуток времени dt:
![]() . (25)
. (25)
Используя допущение об одномерности потока, отнесем все искомые величины к среднему радиусу рассматриваемого лопаточного венца.
Обозначим
массовый расход рабочей среды через венец за единицу времени G. Тогда масса
среды, прошедшая через контрольную поверхность cd за время dt, ![]() .
.
Эта масса займет кольцевой объем dcc'd'. В силу стационарности движения именно такая масса должна содержаться и в объеме abb'a'.
Разложим
произвольно расположенные вектора d(![]() ) и d(
) и d(![]() ) на составляющие относительно осей z и u. Наличие
проекций векторов на направление радиуса не будем принимать во внимание,
поскольку в ступенях с полным подводом рабочей среда их влияние не проявляется.
) на составляющие относительно осей z и u. Наличие
проекций векторов на направление радиуса не будем принимать во внимание,
поскольку в ступенях с полным подводом рабочей среда их влияние не проявляется.
Учитывая одномерность потока и обозначая величины, относящиеся к контрольным поверхностям на входе в венец индексом «вх», а на выходе из венца - индексом «вых», записываем относительно оси z:
![]()
![]() .
.
Поэтому в соответствии с выражением (24):
![]() (26)
(26)
![]() . (27)
. (27)
где ![]() и
и ![]() -
проекции вектора скорости соответственно на направления z и u.
-
проекции вектора скорости соответственно на направления z и u.
Аналогично,
учитывая смысл понятия ![]() и исходя из выражения (25),
получаем:
и исходя из выражения (25),
получаем:
![]() (28)
(28)
![]() . (29)
. (29)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.