6.3. Осевое усилие на венец облопачивания
Осевую
составляющую ![]() всех внешних сил, действующих на контрольную
массу (рис.15), можно представить, в виде суммы равнодействующей сил давления,
действующих на контрольные поверхности,
всех внешних сил, действующих на контрольную
массу (рис.15), можно представить, в виде суммы равнодействующей сил давления,
действующих на контрольные поверхности, ![]() и проекции на
ось z сил,
действующих на контрольную массу со стороны стенок межлопаточных каналов,
и проекции на
ось z сил,
действующих на контрольную массу со стороны стенок межлопаточных каналов, ![]() то есть
то есть
![]() ,
(36)
,
(36)
![]() , (37)
, (37)
где ![]() - давление на контрольную поверхность на
входе в венец,
- давление на контрольную поверхность на
входе в венец,
![]() - давление на контрольную поверхность на
выходе из венца,
- давление на контрольную поверхность на
выходе из венца,
![]() - проекции соответствующих площадей на
плоскость, перпендикулярную оси z.
- проекции соответствующих площадей на
плоскость, перпендикулярную оси z.
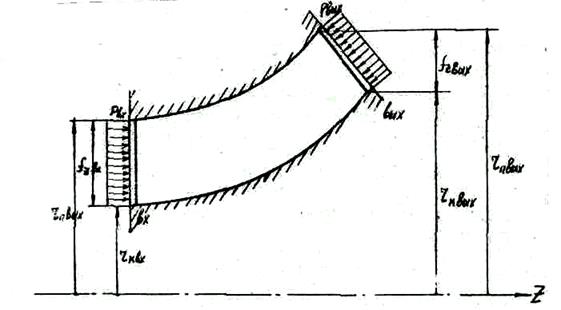
Рис.15. Силы давления, действующие на контрольные поверхности лопаточного венца
Если
обозначить ![]() проекцию на направление z усилия, c которым рабочая
среда действует на рабочий венец, то очевидно равенство
проекцию на направление z усилия, c которым рабочая
среда действует на рабочий венец, то очевидно равенство
![]() , (38)
, (38)
Поэтому выражение (36) изменится следующим образом:
![]() ,
,
с учетом формул (37) и (38)
![]() .
.
По теореме о изменении количества движения
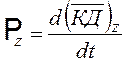 .
.
Учитывая выражение (30), получим:
![]() .
.
Тогда
![]() . (39)
. (39)
Исходя из формулы (39), получим расчетные выражения для определения осевого усилия в сопловом венце:
![]() , (40)
, (40)
а также в рабочем венце
![]() . (41)
. (41)
Расчет
осевого усилия в сопловом венце делается при проверке прочности диафрагмы.
Расчет осевого усилия в рабочем венце необходим не только для расчетов
прочности рабочих лопаток, но и для решения вопроса об обеспечении надежности
работы упорных подшипников. В ступенях с малой степенью реактивности величина ![]() , действующая на рабочий венец, обычно не велика. В
ступенях с большой степенью реактивности примерно половина осевого усилия
приходится на ротор, другая половина - на статор. В этих условиях принимаются
специальные меры для разгрузки упорных подшипников: делаются так называемые
думмисы или выбирается, двухпоточная конструкция проточной части.
, действующая на рабочий венец, обычно не велика. В
ступенях с большой степенью реактивности примерно половина осевого усилия
приходится на ротор, другая половина - на статор. В этих условиях принимаются
специальные меры для разгрузки упорных подшипников: делаются так называемые
думмисы или выбирается, двухпоточная конструкция проточной части.
7. Турбинное уравнение Эйлера
7.1. Мощность и удельная работа
на лопатках (рабочем венце)
При
известных значениях крутящего момента на рабочем венце ![]() и угловой скорости вращения ротора
и угловой скорости вращения ротора ![]() мощность, развиваемая турбинной ступенью,
определяется формулой:
мощность, развиваемая турбинной ступенью,
определяется формулой:
![]() .
.
Подставляя в это
выражение ![]() из полученного ранее выражения
(34), получим:
из полученного ранее выражения
(34), получим:
![]() .
.
Учитывая, что ![]() - окружная скорость рабочих лопаток на
среднем радиусе на входе в венец;
- окружная скорость рабочих лопаток на
среднем радиусе на входе в венец; ![]() - окружная скорость
рабочих лопаток на среднем радиусе на выходе из венца, находим:
- окружная скорость
рабочих лопаток на среднем радиусе на выходе из венца, находим:
![]() . (42)
. (42)
Отнеся эту мощность к I кг рабочего тела, проходящего через венец в единицу времени, получим удельную работу на лопатках:
![]() .
(43)
.
(43)
Выражение (43)
известно в теории турбин как турбинное уравнение Эйлера. Входящее в него
произведение ![]() играет в отношении работы такую же роль,
как произведение
играет в отношении работы такую же роль,
как произведение ![]() в выражении для крутящего
момента. Удельная работа на лопатках
в выражении для крутящего
момента. Удельная работа на лопатках ![]() равна изоэнтропическому
перепаду энтальпий рабочей среды
равна изоэнтропическому
перепаду энтальпий рабочей среды ![]() .
.
7.2. Применение турбинного уравнения Эйлера
Уравнение
(43) получено в результате использования уравнения (32) для производной 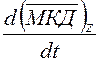 . В связи с этим уравнение Эйлера
справедливо при выполнении допущений, сделанных при выводе уравнения (32). Эти
допущения, идеализирующие течение в лопаточных венцах, в действительности
нарушаются. Степень отклонения действительной картины течения от его идеальной
схемы определяет величину погрешности, связанной с использованием турбинного
уравнения Эйлера. Рассмотрим этот вопрос подробнее.
. В связи с этим уравнение Эйлера
справедливо при выполнении допущений, сделанных при выводе уравнения (32). Эти
допущения, идеализирующие течение в лопаточных венцах, в действительности
нарушаются. Степень отклонения действительной картины течения от его идеальной
схемы определяет величину погрешности, связанной с использованием турбинного
уравнения Эйлера. Рассмотрим этот вопрос подробнее.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.