Числовые характеристики случайных величин, страница 9

Распределение Стьюдента используется для решения вопроса: значимо ли отличие выборочного среднего  от математического ожидания  генеральной совокупности, из которой предположительно взята выборка или наблюдаемое различие является случайным?

3.5.6.3. F – распределение (распределение Фишера – Снедекора).

Если  и  независимые СВ, имеющие  – распределение соответственно с  и  степенями свободы, то случайная величина 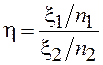 имеет F – распределение с  степенями свободы, ПВ которого имеет вид

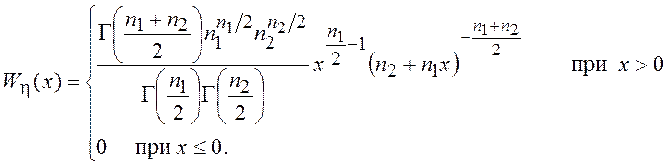
Математическое ожидание 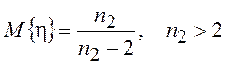, а дисперсия

.

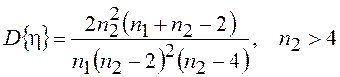Распределение Фишера используется при проверке гипотезы о равенстве дисперсий двух нормальных выборок объемом  и .

3.5.6.4. Логарифмически нормальное (логнормальное) распределение.

Случайная величина x имеет логарифмически нормальное распределение с параметрами  если её ПВ имеет вид

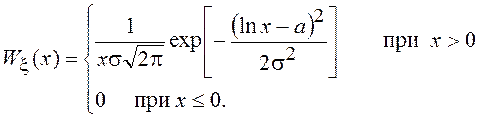
Логнормальное распределение получается как ПВ случайной величины , где h - нормальная СВ с математическим ожиданием а и дисперсией . Решая задачу о функциональном преобразовании СВ, с учетом того что  и 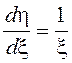 получим для x логнормальное распределение. Условие  при  связано с положительностью функции  для всех h.

Моменты логнормального распределения равны 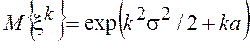, откуда можно найти дисперсию 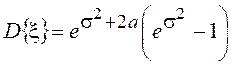, асимметрию  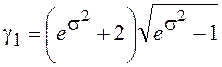и коэффициент эксцесса . Заметим, что СВ x и её моменты являются безразмерными величинами .

Логнормальное распределение дает частный случай решения следующей задачи. Пусть , где h - нормальная СВ с математическим ожиданием а и дисперсией , а  – монотонная дифференцируемая функция. Решая задачу функционального преобразования СВ, получим

,

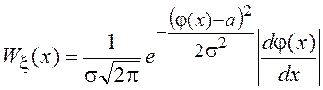где j(х) – функция обратная f(x) (результат решения уравнения  относительно h). Это распределение называется распределением Кептейна.

3.5.6.5. Распределение Релея-Райса.

Рассмотрим задачу о распределении модуля и аргумента нормального случайного вектора , ПВ которого имеет вид

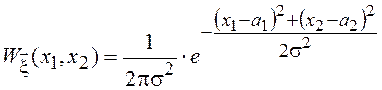 т.е. компоненты вектора  и  независимы, имеют одинаковую дисперсию  и математическое ожидание  и  соответственно.

Модуль вектора , а для аргумента справедливо выражение 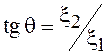. Решая задачу перехода от СВ  и  к r и q с учетом полученных выше результатов , будем иметь

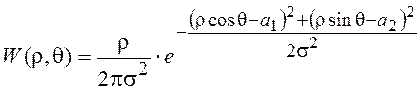
или после несложных преобразований

,

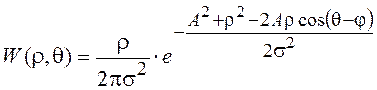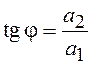где  – модуль вектора, компонентами которого являются математические ожидания СВ  и ,  – аргумент этого вектора. Для определения ПВ r необходимо проинтегрировать  по всем значениям q, т.е.

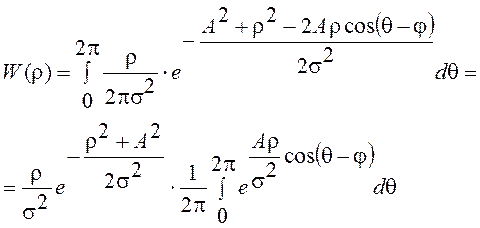
Так как подынтегральное выражение зависит только от  и интегрирование ведется по периоду, то интеграл не зависит от j и с учетом интегрального представления модифицированной функции Бесселя нулевого порядка

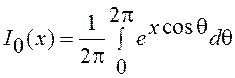, получим окончательно

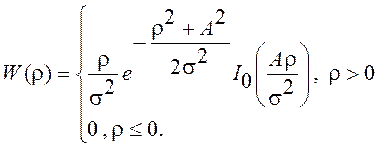
Это и есть распределение Рэлея – Райса. При  =  = 0 и, следовательно, А = 0,   и распределение Рэлея – Райса переходит в распределение Релея

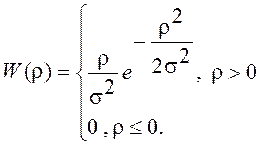
Функция распределения

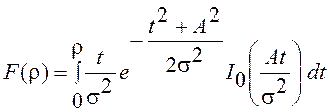
после замены переменной  и введения параметра  выражается через табулированную Q – функцию Маркума 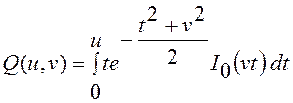 следующим образом

.

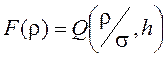Плотность вероятности Рэлея – Райса при переходе к безразмерной переменной 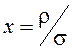 примет вид

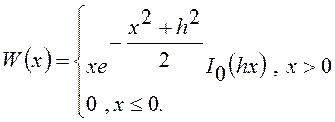
Подумайте, куда делся множитель  ?

При , воспользовавшись асимптотическим представлением модифицированной функции Бесселя

,  ,

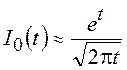после несложных преобразований, будем иметь

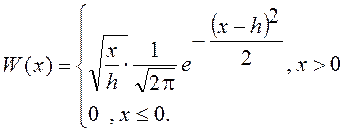
Таким образом, при  распределение Релея – Райса с точностью до поправочного множителя , который при  мало отличается от единицы в той области, где располагается кривая нормального распределения 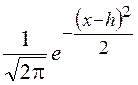, может быть аппроксимировано указанным выше нормальным распределением. При возвращении к переменной r гауссовское распределение будет иметь среднее значение А и дисперсию . В качестве упражнения предлагаем читателю убедиться в том, что множитель  действительно мало отличается от единицы в области основных значений функции 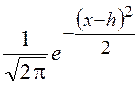[1].

Моменты распределения Релея – Райса  выражаются через вырожденную гипергеометрическую функцию

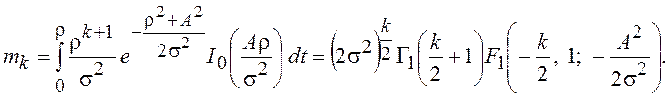
Четные моменты , с учетом свойств вырожденной гипергеометрической функции, см. главу 4, являются полиномами от  и имеют вид

, , ,…