7. Дисперсия произведения
постоянной величины ![]() на СВ
на СВ ![]() равна
равна
![]() . Доказательство этого утверждения
тривиально и предоставляется читателю.
. Доказательство этого утверждения
тривиально и предоставляется читателю.
8. Дисперсия линейной
комбинации 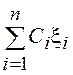 попарно независимых СВ
попарно независимых СВ ![]() равна
равна 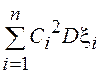 .
Рекомендуем доказать это утверждение самим. Чему равна дисперсия суммы или
разности зависимых СВ, мы определим позднее.
.
Рекомендуем доказать это утверждение самим. Чему равна дисперсия суммы или
разности зависимых СВ, мы определим позднее.
Совершенно аналогично
можно определить моменты (начальные и центральные) для функции ![]() СВ
СВ ![]() , т.е.
, т.е. ![]() =
=![]() =
=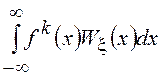 и
и
![]() =
=![]() =
=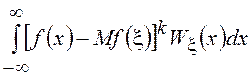 при условии, что
при условии, что 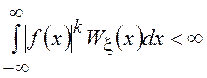 .
.
Между центральными и
начальными моментами существует очевидная связь, определяемая формулой ![]() =
=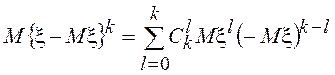 . Используя обозначения
. Используя обозначения
![]() это выражение можно переписать в виде
это выражение можно переписать в виде
![]() =
= .
.
Запишем эту связь для первых четырех центральных моментов, играющих особо важную роль в теории вероятностей и статистике.
![]() =0,
=0,
![]() ,
, ![]() и
и ![]() . На практике обычно используют нормированные
моменты
. На практике обычно используют нормированные
моменты 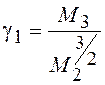 , называемый асимметрией, и
, называемый асимметрией, и 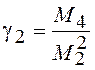 , именуемый эксцессом.
, именуемый эксцессом.
Асимметрия характеризует несимметричность ПВ относительно математического ожидания, рис. 13.
![]()
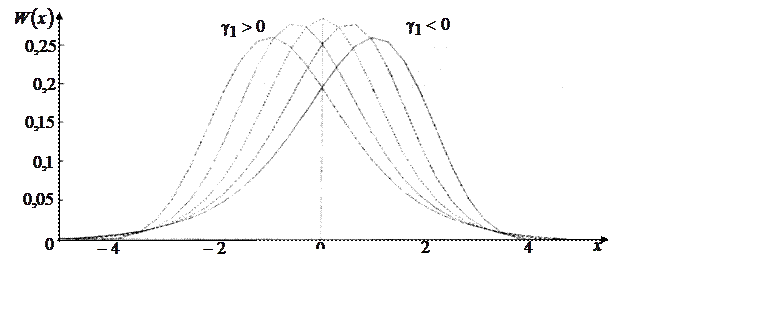 Рис.
13
Рис.
13
Эксцесс ![]() характеризует удельный вес больших
отклонений от математического ожидания или, как говорят в статистике, «тяжесть
хвостов» ПВ. Чаще вместо
характеризует удельный вес больших
отклонений от математического ожидания или, как говорят в статистике, «тяжесть
хвостов» ПВ. Чаще вместо ![]() используют коэффициент
используют коэффициент ![]() =
=![]() -3, который позволяет
сравнивать данную ПВ с гауссовской, для которой
-3, который позволяет
сравнивать данную ПВ с гауссовской, для которой ![]() =3.
Иллюстрация этой зависимости представлена на рис. 14, заимствованном из [18].
=3.
Иллюстрация этой зависимости представлена на рис. 14, заимствованном из [18].
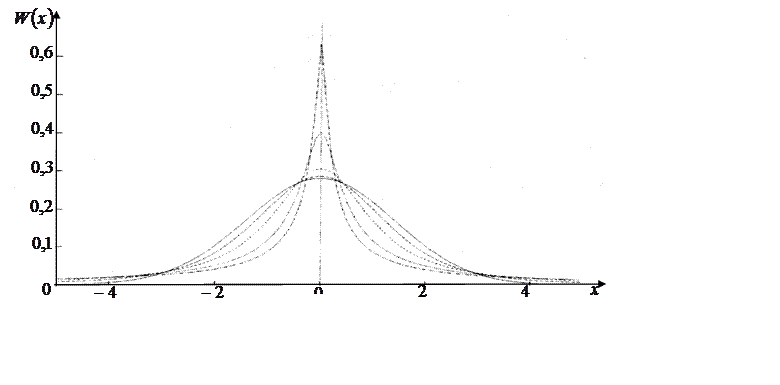
Рис. 14
3.2 Квантили
Моменты СВ являются
удобным способом описания СВ, если они существуют. Однако СВ может и не иметь
моментов. Например, весьма важные для приложений распределение Коши ![]() =
=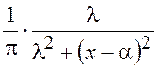 не имеет моментов,
т.к. интеграл
не имеет моментов,
т.к. интеграл 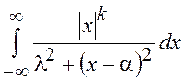 расходится при любых
расходится при любых ![]() =1,2,…
=1,2,…
Кроме того, при экспериментальном определении (оценке) моменты оказываются весьма чувствительными к засорению выборки, т.е. появлению в наблюдаемой совокупности чисел, значений другой СВ, обычно сильно отличающихся по своим свойствам от изучаемой СВ (аномальные ошибки). В этих условиях полезным оказывается использование квантилей, к определению которых мы и переходим.
Определение. Квантильей ![]() -ого
порядка, или
-ого
порядка, или ![]() -квантилью, называют корень уравнения
-квантилью, называют корень уравнения ![]() =
=![]() , обозначаемый как
, обозначаемый как ![]() . При использовании ПВ
. При использовании ПВ ![]() определяется из условия
определяется из условия 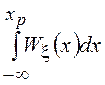 =
=![]() .
.
При ![]() =
=![]() квантиль называют
медианой и обозначают
квантиль называют
медианой и обозначают ![]() =
=![]() . Медиана
определяет точку на оси
. Медиана
определяет точку на оси ![]() , которая делит значения
СВ на две равновероятные половины. Кроме медианы, используют
, которая делит значения
СВ на две равновероятные половины. Кроме медианы, используют ![]() и
и ![]() ,
которые называются квартилями. В качестве характеристики разброса СВ часто
принимается интерквартильный размах или срединное отклонение СВ, равное
,
которые называются квартилями. В качестве характеристики разброса СВ часто
принимается интерквартильный размах или срединное отклонение СВ, равное 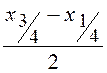 .
.
Полезной характеристикой распределения является мода – абсцисса локального максимума ПВ. По числу мод распределения делятся на унимодальные и полимодальные. Абсцисса глобального максимума называется наивероятнейшим значением СВ.
3.3 Числовые характеристики совокупности случайных величин. Корреляционные моменты
По аналогии с моментами
одномерной СВ ![]() для характеристики совокупности
СВ, случайного вектора
для характеристики совокупности
СВ, случайного вектора ![]() =
=![]() , могут
быть использованы начальные
, могут
быть использованы начальные ![]() и центральные
и центральные ![]() моменты, определяемые как
моменты, определяемые как ![]() =
= 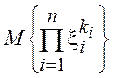 =
=
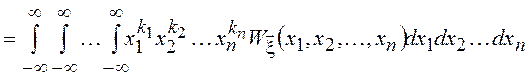
и ![]() =
= 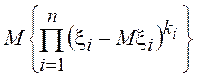 =
=
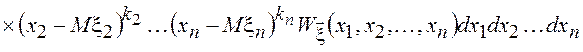 ,
,
где ![]() -
неотрицательные целые числа. Порядком момента называют величину
-
неотрицательные целые числа. Порядком момента называют величину ![]() .
.
Если все показатели
степени ![]() , за исключением одного
, за исключением одного ![]() равны нулю, то приведенные выражения дадут
моменты
равны нулю, то приведенные выражения дадут
моменты ![]() и
и ![]() для СВ
для СВ ![]() . При отличных от нуля двух показателях
степени
. При отличных от нуля двух показателях
степени ![]() и
и ![]() мы
получим характеристику статистической связи СВ
мы
получим характеристику статистической связи СВ ![]() и
и ![]() :
:
![]() =
=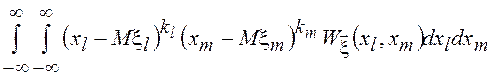 .
.
При ![]() =
=![]() =1 мы приходим к понятию
ковариации СВ
=1 мы приходим к понятию
ковариации СВ ![]() и
и ![]() , характеризующему
меру линейной связи между СВ
, характеризующему
меру линейной связи между СВ ![]() и
и ![]() :
:
![]() =
= ![]() = =
= =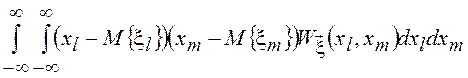 .
.
Чтобы исключить
зависимость ковариации от величины разброса СВ ![]() и
и ![]() относительно средних значений, ее
нормируют относительно их среднеквадратических значений
относительно средних значений, ее
нормируют относительно их среднеквадратических значений ![]() и
и
![]() , т.е. переходят к безразмерному отношению
, т.е. переходят к безразмерному отношению
![]() =
=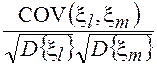 ,
,
называемому коэффициентом корреляции.
Если коэффициент корреляции ![]() равен нулю, то СВ
равен нулю, то СВ ![]() и
и ![]() называют
некоррелированными или ортогональными, т.к. двойной интеграл
называют
некоррелированными или ортогональными, т.к. двойной интеграл 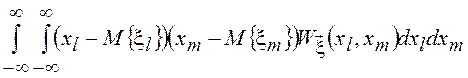 можно рассматривать как скалярное
произведение функций
можно рассматривать как скалярное
произведение функций ![]()
![]() =
=![]()
![]() и
и ![]()
![]() =
=![]()
![]() , в чем легко убедиться, используя аксиомы
скалярного произведения. Тогда, используя неравенство Коши-Буняковского,
получаем, что
, в чем легко убедиться, используя аксиомы
скалярного произведения. Тогда, используя неравенство Коши-Буняковского,
получаем, что ![]() , причем знак равенства
, причем знак равенства ![]() имеет место, если только
имеет место, если только ![]()
![]() =
=![]()
![]()
![]() , или если
, или если ![]() =
=![]()
![]() ,
что означает линейную связь между СВ
,
что означает линейную связь между СВ ![]() и
и ![]() . При этом
. При этом ![]() =
=![]() , где sign – знаковая функция.
, где sign – знаковая функция.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.