Числовые характеристики случайных величин, страница 8

Перейдем теперь к распределениям связанным с нормальными.

3.5.6.1.  – распределение.

К  – распределению можно придти, рассматривая следующую задачу. Пусть  независимые СВ, имеющие стандартное нормальное распределение (среднее значение равно нулю, а дисперсия – единице). Тогда СВ 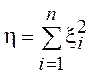 имеет  – распределение с n степенями свободы

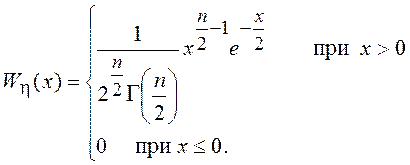
В общем случае параметр n может быть любым положительным числом .

Таким образом, как это уже отмечалось,  – распределение является частным случаем гамма – распределения, рассмотренного выше.  – распределение является одним из, трех важнейших распределений выборочных статистик ( – распределение, распределение Стьюдента и F – распределение). Прежде чем обсуждать эту проблему напомним определение выборочной статистики.

Если  – результаты наблюдений (измерений), полученных в ходе выполнения n независимых повторений случайного эксперимента, связанного со случайной величиной x, имеющей ПВ , которая полностью или частично неизвестна, то вектор  называется выборкой объема n из генеральной совокупности с распределением . Можно дать и более короткое определение [4].

Выборкой называют последовательность независимых одинаково распределенных случайных величин.

Выборочными статистиками или выборочными характеристиками называют функции от выборки (выборочных значений ).

Примерами статистик могут быть выборочные моменты порядка k. Начальные 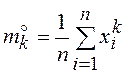 и центральные 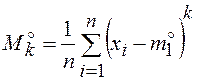. Для выборочных моментов  и  в литературе обычно используют специальные обозначения  и . Отметим, что будучи функцией СВ выборочная статистика является случайной величиной.

Важной задачей статистики является сравнение эмпирического (полученного на основе выборки) и теоретического (или гипотетического) распределений.

Напомним, как строится эмпирическое распределение.

Весь диапазон возможных значений наблюдаемой СВ делится на классы (области), т.е. указывается последовательность примыкающих друг к другу полуинтервалов , причем крайние интервалы  и  являются полубесконечными. Обычно конечные интервалы , их в статистике называют карманами, выбирают одинаковыми. Затем подсчитывают  – число элементов выборки, попавших в полуинтервал  и теоретическую вероятность  попадания результатов измерения в этот интервал

,

где – разбиение интервала, о котором шла речь выше.

После этого вычисляется статистика 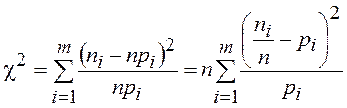, называемая статистикой Пирсона, доказавшим, что при 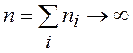 записанная статистика имеет распределение  с  степенью свободы и, что очень важно, не зависит от вида теоретического распределения . Пользуясь таблицами или соответствующими программными пакетами, можно проверить гипотезу о соответствии эмпирического и теоретического распределений [4].

Очевидно, что 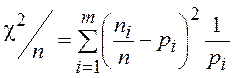 есть евклидово расстояние  между вектором , компонентами которого являются эмпирические частоты попадания наблюдаемых величин в  и вектором , у которого компоненты – теоретические вероятности  попадания наблюдений в .

Компонентами весового вектора  являются величины обратные вероятностям . При практическом использовании критерия согласия χ–квадрат Пирсона для простой гипотезы – так называется рассмотренная задача, надо добиваться за счет n и выбора числа карманов m, чтобы для всех выполнялось бы условие .

3.5.6.2. Распределение Стьюдента. (t – распределение)

Рассмотрим СВ , где x и z – независимые СВ, причем x имеет стандартное нормальное распределение , а z –  – распределение с n степенями свободы. Тогда ПВ случайной величины h имеет вид

,

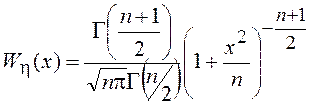и называется распределением Стьюдента с n степенями свободы. При n= 1 распределение Стьюдента переходит в уже знакомое нам распределение Коши. Распределение Стьюдента распространяется и на случай нецелых значений n = a >0.

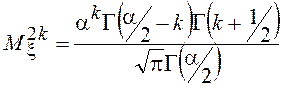Моменты распределения Стьюдента равны  и  при . Вспомним, что распределение Коши моментов не имеет.