Выясним связь между
понятиями независимость СВ и их некоррелированность. Если СВ ![]() и
и ![]() независимы,
то они некоррелированы, т.к. в этом случае
независимы,
то они некоррелированы, т.к. в этом случае
![]()
![]() =
=![]()
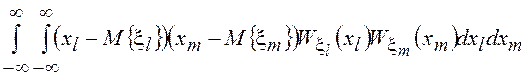
![]() =
=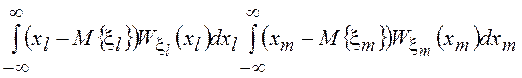
![]() =
=![]()
![]()
![]() =
0.
=
0.
Обратное утверждение в
общем случае не имеет места. Например, если ![]() =
=![]() и
и ![]() =
=![]() , где
, где ![]() - СВ,
равномерно распределенная в интервале
- СВ,
равномерно распределенная в интервале ![]() , то
, то ![]()
![]() =
=![]()
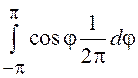
![]() =
=![]()
![]()
![]() =
=![]()
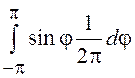
![]() = 0 и
= 0 и ![]()
![]() =
=![]()
![]() =
=![]()
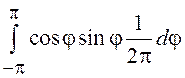
![]() =
=![]()
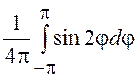
![]() = 0, т.е.
= 0, т.е. ![]() и
и ![]() - некоррелированные СВ, но между ними
существует функциональная связь
- некоррелированные СВ, но между ними
существует функциональная связь ![]() =1 (но не линейная!).
=1 (но не линейная!).
3.4. Кумулянты.
Еще одним видом числовых характеристик СВ являются кумулянты или семиинварианты. В ряде случаев их использование оказывается более эффективным, чем описание СВ с помощью моментов. Прежде чем дать определение кумулянтам, остановимся на свойствах введенной выше ХФ
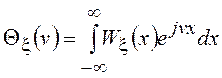 .
.
Прежде всего, отметим,
что 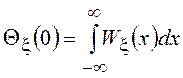 =1. ХФ
=1. ХФ ![]() непрерывна
для всех
непрерывна
для всех ![]() , для нее выполняются следующие условия:
, для нее выполняются следующие условия: ![]() ;
; ![]() и
и 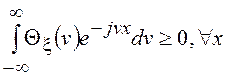 , где
, где ![]() - знак
комплексного сопряжения. Производная
- знак
комплексного сопряжения. Производная ![]() -ого порядка
характеристической функции в нуле
-ого порядка
характеристической функции в нуле 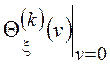 =
=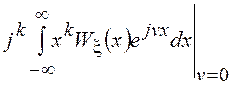 =
=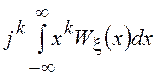 =
=![]() позволяет определить
позволяет определить ![]() -ый начальный момент СВ
-ый начальный момент СВ ![]() . Таким образом, характеристическая функция
может быть представлена рядом Маклорена
. Таким образом, характеристическая функция
может быть представлена рядом Маклорена
![]() =
=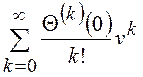 =
=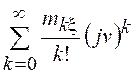 ,
,
где ![]() =
=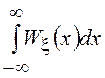 =1.
=1.
Логарифм ХФ ![]() =
=![]() называется кумулянтной
функцией. Разлагая кумулянтную функцию в ряд Маклорена, получим
называется кумулянтной
функцией. Разлагая кумулянтную функцию в ряд Маклорена, получим
![]() =
=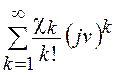 ,
,
где ![]() -
кумулянты или семиинварианты распределения
-
кумулянты или семиинварианты распределения ![]() .
.
Кумулянты ![]() выражаются через моменты СВ
выражаются через моменты СВ ![]() :
:
![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,…
,…
Для дальнейшего нам потребуется завершить знакомство с нормальной СВ, рассмотренной в первом приближении в примере 4 раздела 1.
Как было указано выше,
пример нормальной СВ ![]() имеет вид
имеет вид
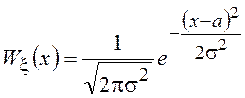 .
.
Характеристическая функция, в соответствии со свойствами преобразования Фурье, будет равна
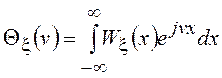 =
=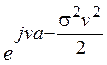 .
.
Математическое ожидание
нормальной СВ ![]() вычисляется как
вычисляется как ![]() =
=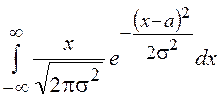 . Выполняя замену
переменной
. Выполняя замену
переменной 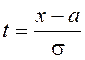 , получим
, получим
![]() =
=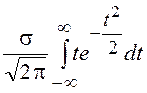 +
+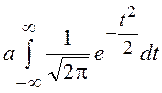 .
.
Первый интеграл равен
нулю, как интеграл от нечетной функции в симметричных пределах, а второй –
единице по условию нормировки (под знаком интеграла стоит ПВ стандартной
нормальной СВ ![]() , имеющей нулевое математическое
ожидание и единичную дисперсию).
, имеющей нулевое математическое
ожидание и единичную дисперсию).
Таким образом, параметр ![]() имеет смысл математического ожидания
нормальной СВ,
имеет смысл математического ожидания
нормальной СВ, ![]() =
=![]() .
.
Центральные моменты нормальной СВ равны
![]() =
=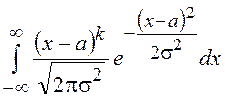 ,
,
или после замены переменной 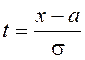 имеем
имеем ![]() =
=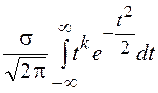 .
.
Учитывая четность при ![]() и нечетность при
и нечетность при ![]() ,
,
![]() =0,1,2,… подинтегрального выражения,
получим окончательно
=0,1,2,… подинтегрального выражения,
получим окончательно
![]() и
и ![]() =
=![]() ,
, ![]() =1,2,…
=1,2,…
Напомним, что ![]() всегда равняется нулю.
всегда равняется нулю.
Полагая ![]() =1, получим
=1, получим ![]() =
=![]() , т.е. параметр
, т.е. параметр ![]() есть
дисперсия нормальной СВ.
есть
дисперсия нормальной СВ.
Асимметрия нормального
распределения 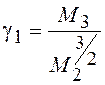 и коэффициент эксцесса
и коэффициент эксцесса 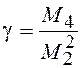 – 3=
– 3=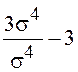 равны
нулю.
равны
нулю.
Кумулянты нормального
распределения ![]() , начиная с
, начиная с ![]() , также равны нулю;
, также равны нулю; ![]() =
=![]() и
и ![]() =
=![]() , поэтому кумулянты, точнее кумулянтные коэффициенты
, поэтому кумулянты, точнее кумулянтные коэффициенты
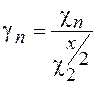 =
=![]() , характеризуют степень
отличия рассматриваемого распределения от гауссовского.
, характеризуют степень
отличия рассматриваемого распределения от гауссовского.
Это находит свое отражение в возможности представления произвольной ПВ с помощью ряда Эджворта
![]() =
=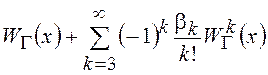 ,
,
где ![]() =
=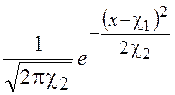 - гауссовское распределение, имеющее
- гауссовское распределение, имеющее ![]() =
=![]() и
и ![]() =
=![]() , а коэффициенты
, а коэффициенты ![]() , называемые квазимоментами, выражаются через
кумулянты распределения
, называемые квазимоментами, выражаются через
кумулянты распределения ![]() следующим образом:
следующим образом:
![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,…
,…
Квазимоменты отличны от нуля только для негауссовских СВ.
Кумулянты могут быть
определены и для многомерных СВ. Чтобы избежать громоздких записей, рассмотрим
случай двух СВ ![]() и
и ![]() , являющихся
компонентами, или координатами случайного вектора
, являющихся
компонентами, или координатами случайного вектора ![]() . Для
двумерного распределения
. Для
двумерного распределения ![]() смешанные начальные и
центральные моменты имеют вид
смешанные начальные и
центральные моменты имеют вид
![]() =
=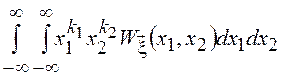 и
и
![]() =
=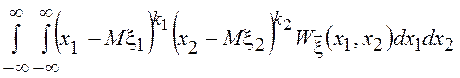 .
.
Характеристическая функция двумерной СВ
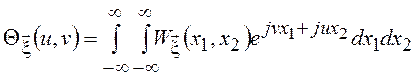
может быть разложена в двойной степенной ряд вида
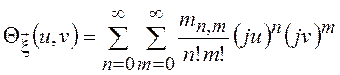 .
.
Разложение ![]() в степенной ряд
в степенной ряд
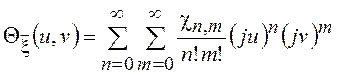 .
.
определяет совместные кумулянты ![]() двумерного распределения
двумерного распределения ![]() . Как и для моментов, сумма
. Как и для моментов, сумма ![]() определяет порядок кумулянта
определяет порядок кумулянта ![]() . Совместные кумулянты выражаются через
моменты следующим образом:
. Совместные кумулянты выражаются через
моменты следующим образом:
![]() ,
,
где для удобства записи под ![]() и
и ![]() понимаются
понимаются
![]() -ые начальные моменты одномерных
распределений
-ые начальные моменты одномерных
распределений ![]() и
и ![]() , т.е.
, т.е.
![]()
![]() =
=![]()
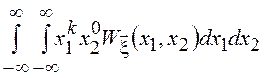
![]() =
=![]()
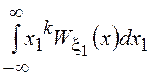
![]() =
=![]()
![]() .
.
Аналогичная запись
справедлива и для ![]() . Из приведенной записи видно,
что
. Из приведенной записи видно,
что ![]() совпадает с ковариацией СВ
совпадает с ковариацией СВ ![]() и
и ![]() , т.к.
, т.к.
![]()
![]() =
=![]()
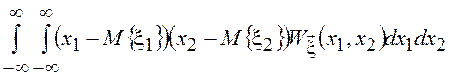
![]() = =
= =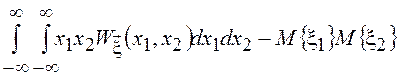
![]() =
=![]()
![]() .
.
Две СВ являются
статистически зависимыми или просто зависимыми, если хотя бы один из совместных
кумулянтов ![]() ,
, ![]() отличен
от нуля.
отличен
от нуля.
3.5. Числовые характеристики некоторых распространенных распределений случайных величин
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.