Числовые характеристики случайных величин, страница 10

Для нечетных k вырожденная гипергеометрическая функция может быть представлена с помощью экспоненциальных и модифицированных  бесселевых функций и мы получим

.

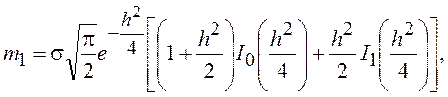
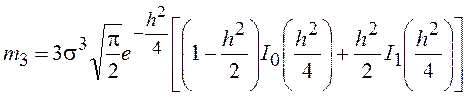При   как уже отмечалось, распределение Рэлея – Райса переходит в распределение Рэлея, а приведенные формулы определяют соответствующие моменты 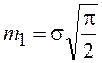, , ,  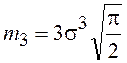и т.д.

Пользуясь связью между центральными и начальными моментами, можно определить дисперсию

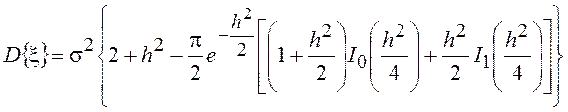
для распределения Рэлея – Райса и 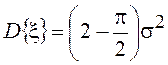 для распределения Рэлея.

В качестве упражнения предлагаем исследовать зависимость асимметрии и коэффициента эксцесса распределения Рэлея – Райса от параметра h.

В теории надежности для описания времени безотказной работы используется распределение Вейбулла-Гнеденко, ПВ которого имеет вид

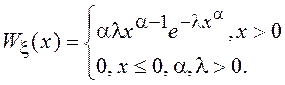
Моменты  равны 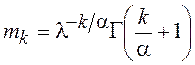. С их помощью можно найти дисперсию

.

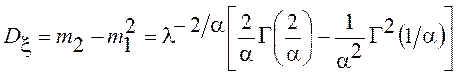Для описания модели замираний сигнала в канале часто используют распределение Накагами (m – распределение) с ПВ

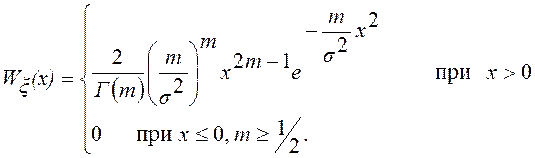
Моменты распределения Накагами

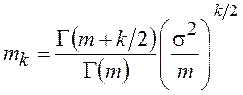, а дисперсия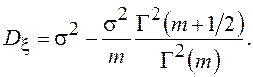

Заканчивая разговор об одномерных ПВ, отметим, что большинство из рассмотренных выше распределений является частным случаем распределения Пирсона, ПВ которого удовлетворяет дифференциальному уравнению вида

,

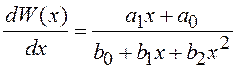где  – параметры распределения.

В зависимости от значений этих параметров в качестве решения уравнения получаются 11 типов кривых, описывающих важнейшие ПВ (нормальное распределение, гамма, бета,  – распределение, распределение Стьюдента и др.) Более подробно с распределениями пирсоновского типа можно познакомиться с помощью [5].

3.6. Многомерные распределения.

3.6.1. Полиномиальное распределение.

Полиномиальное распределение является многомерным аналогом биномиального распределения, когда исходом случайного эксперимента могут быть не два (как в биномиальном законе), а k исходов с вероятностями 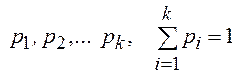. При проведении N независимых испытаний нас интересует вероятность того, что i–й исход имел место ровно  раз, .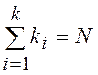

Таким образом полиномиальное распределение дает вероятность того, что целочисленные компоненты вектора  будут равны одноименным компонентам вектора , а именно 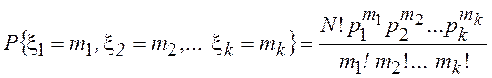. При k = 2 это распределение естественно переходит в биномиальное.

Математическое ожидание вектора  равно . Ковариация СВ  и ,  равна , а дисперсия i – ой компоненты вектора  . Следовательно,  =.

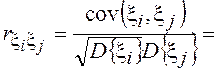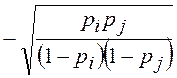3.6.2. Многомерное нормальное распределение.

Случайный вектор  имеет нормальное распределение, т.е. является нормальным случайным вектором, если его ХФ  имеет вид 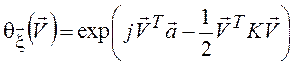, где  – вектор средних значений, K – неотрицательно определенная симметрическая  матрица, Т – как и раньше, знак транспонирования. Если , то распределение называется невырожденным. Для невырожденного распределения матрицу  называют матрицей точности. Элементами матрицы K, называемой ковариационной или чаще корреляционной являются ковариации соответствующих компонент вектора , т.е. , где .

Многомерное нормальное распределение, отвечающее введенной ХФ имеет вид

.

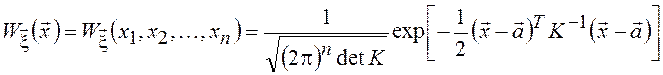Отметим важнейшие свойства многомерного нормального распределения.

1. Если компоненты вектора  некоррелированы т.е. , , то корреляционная матрица К будет диагонально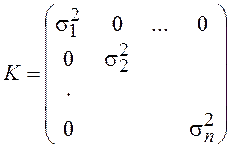й  и 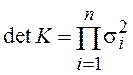. Так же диагональной будет и обратная матрица, и многомерное нормальное распределение примет вид

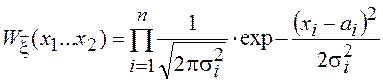
Таким образом некоррелированность нормальных СВ влечет их независимость.

2. Если нас интересует совместное распределение части, компонент нормального случайного вектора , например, вектора , , то интегрируя  по исключаемым компонентам , получим снова многомерное нормальное распределение с вектором средних значений  и корреляционной матрицей .

3. Линейное преобразование нормального случайного вектора.

Пусть вектор  связан с вектором  линейным преобразованием (получен с помощью линейного оператора). В главе 5 первой части пособия было показано, что в  или  действие любого линейного оператора сводится к умножению исходного вектора на матрицу оператора, т.е. .