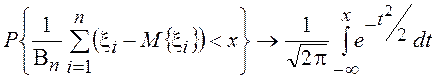 ,
,
где 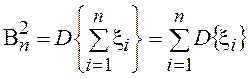 .
Поэтому становится ясным, почему распределение суммы независимых СВ,
подчиняющихся распределению Коши, не имеющему моментов, не стремятся к
нормальному закону.
.
Поэтому становится ясным, почему распределение суммы независимых СВ,
подчиняющихся распределению Коши, не имеющему моментов, не стремятся к
нормальному закону.
Как и распределение Коши, нормальное распределение является устойчивым: распределение суммы независимых нормальных СВ будет нормальным с математическим ожиданием и дисперсией, равными сумме математических ожиданий и дисперсий слагаемых соответственно. Позже мы убедимся в том, что СВ будет гауссовской и для зависимых слагаемых.
Для знакомства с
распределениями, связанными с нормальным, нам потребуется информация о
двумерном нормальном законе, распределении двумерного нормального случайного
вектора ![]() .
.
В соответствии с общей формой записи многомерного нормального распределения
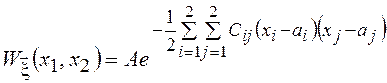 .
.
Элементы ![]() квадратичной формы определяются обратной
корреляционной матрицей
квадратичной формы определяются обратной
корреляционной матрицей ![]() , где
, где 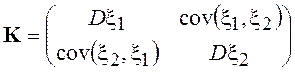 - симметричная и положительно
определенная. Дисперсия СВ обычно обозначается как
- симметричная и положительно
определенная. Дисперсия СВ обычно обозначается как ![]() , поэтому
корреляционная матрица имеет вид
, поэтому
корреляционная матрица имеет вид
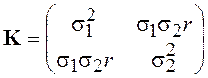 ,
,
где ![]() - коэффициент корреляции, а
- коэффициент корреляции, а
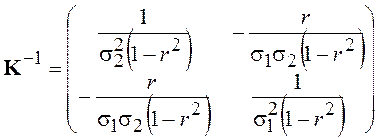 .
.
Константа ![]() определяется из условия нормировки и равна
определяется из условия нормировки и равна
![]() =
=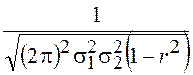 . Окончательное
выражение для двумерного нормального распределения имеет вид
. Окончательное
выражение для двумерного нормального распределения имеет вид
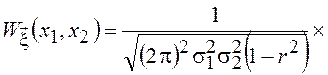
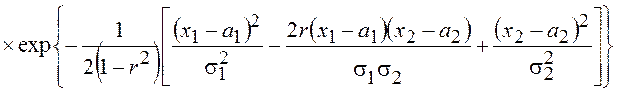 , где
, где
![]() =
=![]() и
и ![]() =
=![]() - математические ожидания СВ
- математические ожидания СВ ![]() и
и ![]() ,
, ![]() и
и ![]() - их дисперсии, а
- их дисперсии, а ![]() - коэффициент взаимной корреляции.
- коэффициент взаимной корреляции.
Найдем ПВ суммы двух
нормальных СВ ![]() . В соответствии с полученными выше результатами
. В соответствии с полученными выше результатами
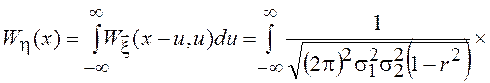
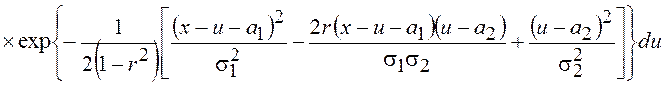
Выполнив элементарные преобразования и интегрирование по u, получим окончательно
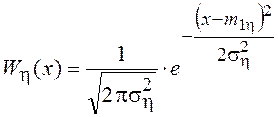 ,
,
где ![]() - математическое ожидание суммы СВ x1 и x2 , а
- математическое ожидание суммы СВ x1 и x2 , а ![]() - её (суммы) дисперсия. Таким
образом в общем случае, распределение суммы двух нормальных СВ есть нормальная
СВ. Этот результат справедлив и для произвольного числа слагаемых.
- её (суммы) дисперсия. Таким
образом в общем случае, распределение суммы двух нормальных СВ есть нормальная
СВ. Этот результат справедлив и для произвольного числа слагаемых.
Мы уже отмечали, что зная
многомерную ПВ ![]() , можно найти ПВ подмножества СВ
, можно найти ПВ подмножества СВ ![]() проинтегрировав
проинтегрировав ![]() по «лишним» переменным. Для
двумерного случая это даст
по «лишним» переменным. Для
двумерного случая это даст
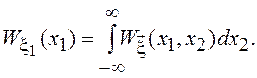
Воспользуемся этой формулой в нашем случае
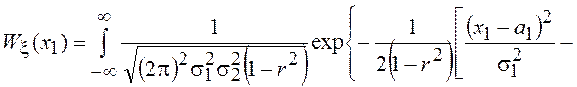
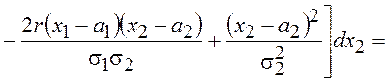
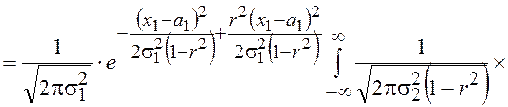
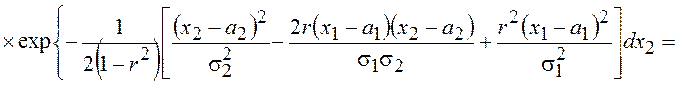
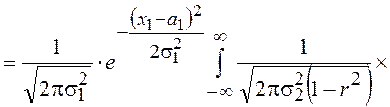
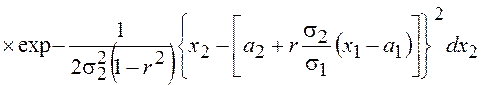
Учитывая, что под знаком
интеграла по ![]() стоит гауссовская ПВ с математическим ожиданием
стоит гауссовская ПВ с математическим ожиданием 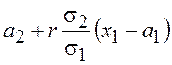 и дисперсией
и дисперсией ![]() , с учетом условия нормировки получим
окончательно
, с учетом условия нормировки получим
окончательно
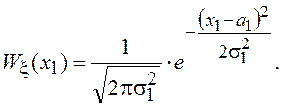
Таким образом, если случайные величины являются совместно нормальными, то каждая из них будет также нормальной. Обратное утверждение в общем случае несправедливо. Гауссовы СВ могут образовывать негауссову совокупность [3].
Пользуясь полученными результатами, легко найти условную ПВ нормальной СВ
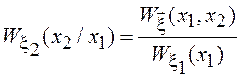
(это выражение обычно рассматривают
как определение условной ПВ). Подставляя в эту формулу выражение для ![]() и
и
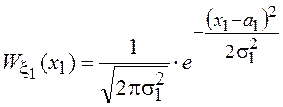 ,
,
после несложных преобразований будем иметь
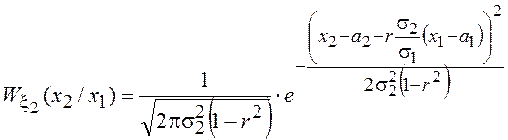
Таким образом, условная
гауссовская ПВ также является гауссовской с условным математическим ожиданием 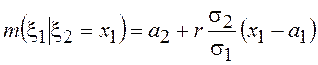 и условной дисперсией
и условной дисперсией ![]() . Из приведенных выражений видно, что
для гауссовских СВ кривая регрессии
. Из приведенных выражений видно, что
для гауссовских СВ кривая регрессии ![]() на
на ![]() есть прямая. При
есть прямая. При ![]() условная ПВ стремится к
условная ПВ стремится к 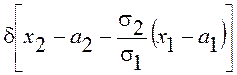 , что совершенно естественно, так как
при
, что совершенно естественно, так как
при ![]() СВ
СВ ![]() и
и ![]() связаны линейной зависимостью
связаны линейной зависимостью ![]() . При
. При ![]() условная ПВ
условная ПВ ![]() переходит в безусловную
переходит в безусловную
 ,
,
 что свидетельствует о независимости СВ
что свидетельствует о независимости СВ ![]() и
и ![]() . Это свойство сохраняется и для многомерных
нормальных СВ, т.е. если нормальные СВ некоррелированы, то они и независимы. На
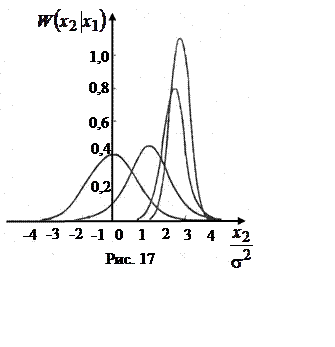
рис. 17 приведено семейство условных ПВ
. Это свойство сохраняется и для многомерных
нормальных СВ, т.е. если нормальные СВ некоррелированы, то они и независимы. На
рис. 17 приведено семейство условных ПВ ![]() для
различных значений коэффициента корреляции
для
различных значений коэффициента корреляции ![]() и
и ![]() =
=![]() = 0,
= 0, ![]() =
=![]() = 1.
= 1.
Рассмотрим область на
плоскости ![]() ,
, ![]() , для
которой
, для
которой ![]() , где
, где ![]() , а
, а ![]() - максимальное значение двумерного нормального распределения,
- максимальное значение двумерного нормального распределения, 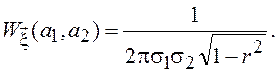 Границей этой области будет эллипс
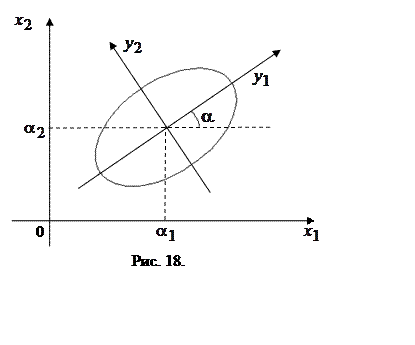
Границей этой области будет эллипс
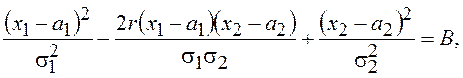
где 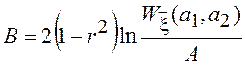 ,
приведенный на рис. 18.
,
приведенный на рис. 18.
Центр этого эллипса расположен
в точке ![]() , а полуоси наклонены по отношению к координатным
осям
, а полуоси наклонены по отношению к координатным
осям ![]() ,
, ![]() на угол
на угол
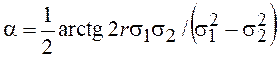 при
при ![]() и
и 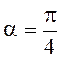 при
при ![]() . При
. При ![]() и
и ![]() эллипс
переходит в окружность.
эллипс
переходит в окружность.
Если перейти от СВ ![]() и
и ![]() к СВ
к СВ ![]() ,
, ![]() с
помощью линейного преобразования
с
помощью линейного преобразования
![]() ,
,
![]()
 что соответствует применению оператора поворота на угол a к случайному вектору
что соответствует применению оператора поворота на угол a к случайному вектору ![]() и переносу начала координат в точку
и переносу начала координат в точку ![]() , то СВ
, то СВ ![]() и
и ![]() , оставаясь нормальными, будут
некоррелированы, а, следовательно, и независимы.
, оставаясь нормальными, будут
некоррелированы, а, следовательно, и независимы.
Таким образом, с помощью линейного преобразования коррелированные нормальные СВ могут быть преобразованы в некоррелированные СВ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.