2.
В условиях
предыдущей задачи путем взятия однократного отсчета было получено значение ![]() . Найдите отношение правдоподобия. Каким
должен быть порог для принятия решения согласно критерию максимального
правдоподобия? Какое решение будет принято оптимальным демодулятором в данном
случае?
. Найдите отношение правдоподобия. Каким
должен быть порог для принятия решения согласно критерию максимального
правдоподобия? Какое решение будет принято оптимальным демодулятором в данном
случае?
3.
В условиях задачи
1 известно, что априорная вероятность присутствия сигнала в смеси ![]() составляет 0,05, а СКО
составляет 0,05, а СКО ![]() . Найдите порог, оптимальный по критерию
идеального наблюдателя. Определите, какое должно быть принято решение при
. Найдите порог, оптимальный по критерию
идеального наблюдателя. Определите, какое должно быть принято решение при ![]() ; при
; при ![]() .
.
4.
В дополнение к
условиям предыдущей задачи учтите, что потери в случае пропуска сигнала в 20 раз выше, чем в случае ложной тревоги. Определите порог, оптимальный по критерию
Байеса. Определите, какое должно быть принято решение при ![]() ; при
; при ![]() .
.
5.
На выходе
аналогового канала наблюдается колебание ![]() ,
представляющее собой либо шум
,
представляющее собой либо шум ![]() , либо сумму сигнала
, либо сумму сигнала ![]() с шумом. Считая шум гауссовским с нулевым
средним и СКО
с шумом. Считая шум гауссовским с нулевым
средним и СКО ![]() , а сигнал – прямоугольным
видеоимпульсом амплитуды
, а сигнал – прямоугольным
видеоимпульсом амплитуды ![]() , запишите отношение
правдоподобия для выборки объема
, запишите отношение
правдоподобия для выборки объема ![]() в пределах длительности
импульса (отсчеты шума считайте некоррелированными). Запишите отношение правдоподобия
для случая, когда сигнал имеет форму импульса, показанного на Рис. 15, а отсчеты смеси берутся равномерно
в пределах интервала
в пределах длительности
импульса (отсчеты шума считайте некоррелированными). Запишите отношение правдоподобия
для случая, когда сигнал имеет форму импульса, показанного на Рис. 15, а отсчеты смеси берутся равномерно
в пределах интервала ![]() . Какие отсчеты учитываются с
большим весом (с большим «доверием»)?
. Какие отсчеты учитываются с
большим весом (с большим «доверием»)?

Рис. 15
6.
Принимаемый сигнал
представляет собой радиоимпульс амплитуды ![]() с
неизвестной начальной фазой, наблюдаемый на фоне аддитивного гауссовского шума
с нулевым средним и СКО
с
неизвестной начальной фазой, наблюдаемый на фоне аддитивного гауссовского шума
с нулевым средним и СКО ![]() . Запишите отношение
правдоподобия для однократного отсчета напряжения на выходе детектора
огибающей. Определите порог, оптимальный по критерию максимального правдоподобия.
. Запишите отношение
правдоподобия для однократного отсчета напряжения на выходе детектора
огибающей. Определите порог, оптимальный по критерию максимального правдоподобия.
7.
Принимаемый
сигнал представляет собой радиоимпульс амплитуды ![]() с
неизвестной начальной фазой, наблюдаемый на фоне аддитивного гауссовского шума
с нулевым средним и дисперсией
с
неизвестной начальной фазой, наблюдаемый на фоне аддитивного гауссовского шума
с нулевым средним и дисперсией ![]() . Запишите отношение
правдоподобия для однократного отсчета напряжения на выходе детектора
огибающей. Определите порог, оптимальный по критерию Неймана–Пирсона при
заданном уровне вероятности ложной тревоги
. Запишите отношение
правдоподобия для однократного отсчета напряжения на выходе детектора
огибающей. Определите порог, оптимальный по критерию Неймана–Пирсона при
заданном уровне вероятности ложной тревоги ![]() .
.
8.
Некоторое
упрощение некогерентного приемника может быть достигнуто исключением операции
извлечения квадратного корня из суммы квадратов квадратурных компонент, которая
имеет в отсутствие сигнала распределение ![]() с 2
степенями свободы, совпадающее с экспоненциальным распределением с плотностью
с 2
степенями свободы, совпадающее с экспоненциальным распределением с плотностью
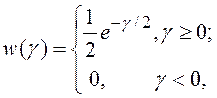 а
при наличии сигнала – нецентральное распределение
а
при наличии сигнала – нецентральное распределение ![]() с 2
степенями свободы. Определите порог для такого приемника, оптимальный по
критерию Неймана–Пирсона при заданном уровне вероятности ложной тревоги
с 2
степенями свободы. Определите порог для такого приемника, оптимальный по
критерию Неймана–Пирсона при заданном уровне вероятности ложной тревоги ![]() .
.
9.
Найдите
импульсную характеристику согласованного фильтра для приема радиоимпульса прямоугольной
формы и длительности ![]() (начальная фаза высокочастотного
заполнения равна
(начальная фаза высокочастотного
заполнения равна ![]() ). Определите форму отклика
согласованного фильтра на этот сигнал.
). Определите форму отклика
согласованного фильтра на этот сигнал.
10. Найдите импульсную характеристику согласованного фильтра для приема радиоимпульса пилообразной формы с огибающей, показанной на Рис. 15 (начальная фаза высокочастотного заполнения равна 0). Определите форму отклика согласованного фильтра на этот сигнал.
11. Определите форму отклика фильтра, согласованного с прямоугольным радиоимпульсом, на пилообразный радиоимпульс Рис. 15, и наоборот.
1.
При неравномерном
квантовании сигналов для импульсно-кодовой модуляции в США и Японии применяется
![]() -аппроксимация характеристики компрессора
-аппроксимация характеристики компрессора
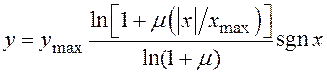 ,
,
где ![]() ,
, ![]() и
и ![]() – напряжения на входе и выходе
компрессора,
– напряжения на входе и выходе
компрессора, ![]() и
и ![]() – их
максимальные (амплитудные) значения, а функция
– их
максимальные (амплитудные) значения, а функция ![]() определяется
выражением
определяется
выражением 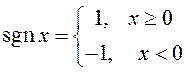 . Постройте график характеристики компрессора для
. Постройте график характеристики компрессора для ![]() .
.
2.
Европейский
стандарт для ИКМ предусматривает компрессию по ![]() -закону,
определяемому выражением
-закону,
определяемому выражением
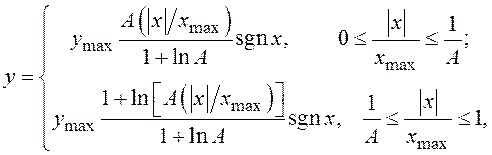
где ![]() .
Постройте график разности
.
Постройте график разности ![]() - и
- и ![]() -аппроксимаций.
-аппроксимаций.
3. После компрессии исходный сигнал подвергается равномерному квантованию на 256 уровней. Определите количество уровней квантования, приходящееся на линейный участок характеристики компрессора, соответствующего европейскому стандарту.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.