Теория электрической связи: Сборник задач и упражнений, страница 5

5.  Составьте дифференциальное уравнение -фильтра верхних частот (дифференцирующей цепочки). Выведите КЧХ и передаточную функцию цепи. Найдите импульсную характеристику цепи.

6.  Найдите низкочастотный эквивалент колебательного контура, если его комплексное сопротивление описывается выражением
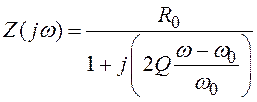, где  – сопротивление на резонансной частоте ,  – добротность контура.

7.   На вход ЛИС-цепи с АЧХ вида 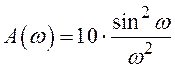 и ФЧХ вида  воздействуют (по отдельности) сигналы вида:

Напишите выражения для выходных сигналов.

5. ПРИНЦИПЫ МОДУЛЯЦИИ И ДЕМОДУЛЯЦИИ

1.  Вольтамперная характеристика (ВАХ) нелинейного элемента задана в виде таблицы

Постройте график ВАХ. Определите коэффициенты аппроксимирующего полинома второй степени.

2.  Вольтамперная характеристика нелинейного элемента задана в виде таблицы

Постройте график ВАХ. Определите параметры  и  аппроксимирующей функции вида .

3.  Вольтамперная характеристика нелинейного элемента задана в виде таблицы

Постройте график ВАХ. Определите параметры  и  аппроксимирующей функции вида .

4.  Напряжение, приложенное к параметрическому линейному элементу с переменной проводимостью , изменяется по гармоническому закону . Определите коэффициент амплитудной модуляции тока, протекающего через элемент.

5.  В качестве параметрического линейного элемента можно использовать нелинейный элемент (в частности, полупроводниковый диод), если сигнал, подлежащий преобразованию, имеет малую амплитуду. При этом в малой окрестности рабочей точки ВАХ аппроксимируется линейной функцией; тогда управление крутизной осуществляется приложением к диоду медленно меняющегося напряжения, смещающего рабочую точку по характеристике. Определите закон изменения крутизны в окрестности рабочей точки, если ВАХ описывается квадратичным полиномом , а управляющее напряжение изменяется по закону .

6.  Определите закон изменения крутизны в окрестности рабочей точки, если ВАХ диода описывается полиномом , а управляющее напряжение – выражением . Определите спектр тока, протекающего через диод, если к диоду, кроме управляющего напряжения, приложено напряжение , .

7.  Определите качественно спектр тока, протекающего через полупроводниковый диод, если к нему приложена сумма низкочастотного (например, речевого) сигнала и управляющего напряжения, имеющего форму меандра (периодического прямоугольного колебания скважности 2) с частотой, намного превышающей верхнюю частоту спектра НЧ сигнала. Можно ли использовать этот принцип для получения амплитудно-модулированных сигналов?   

6. ЦЕПИ С ОБРАТНОЙ СВЯЗЬЮ

1.  Составьте схему цепи с обратной связью, считая, что прямой канал представляет собой идеальный усилитель с коэффициентом усиления , не зависящим от частоты, а цепь обратной связи содержит последовательно включенные линию задержки на величину  («запаздывающая» обратная связь) и безынерционное линейное звено с коэффициентом передачи . Найдите амплитудно-частотную характеристику цепи с обратной связью и постройте графики при ; при ; при . (При значениях , близких к 1, эта цепь представляет собой так называемый гребенчатый фильтр).