Теория электрической связи: Сборник задач и упражнений, страница 3

Убедитесь в том, что полученная структура , называемая полем Галуа по модулю 2, действительно является полем.

35.  Последовательность нулей и единиц фиксированной длины  можно рассматривать как вектор. Определите, сколько существует различных векторов такого вида. Убедитесь непосредственной проверкой аксиом в том, что множество всех таких векторов становится линейным пространством, если на нем определить операции поразрядного сложения (по модулю 2) векторов, а также умножения векторов на скаляры из поля .

36.   Убедитесь, что операция, ставящая в соответствие паре двоичных векторов  и  скаляр 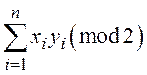 обладает свойствами скалярного произведения, если сумма понимается по модулю 2.

37.  Метрика (расстояние) Хэмминга определяется на пространстве двоичных векторов длины  выражением 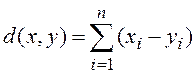, где вычитание понимается по модулю 2, а сложение в обычном смысле. Определите максимальное и минимальное значение расстояния между всевозможными парами векторов.

38.   Найдите автокорреляционную функцию пилообразного импульса, показанного на Рис. 5.

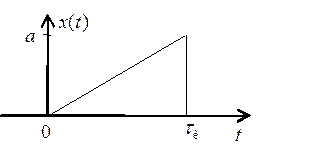
Рис. 5

39.  Найдите взаимно корреляционную функцию пилообразного импульса (Рис. 5) и прямоугольного видеоимпульса такой же длительности и амплитуды.

40.  Определите спектральную плотность колокольного импульса 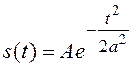. (Воспользуйтесь приемом, называемым приведением к полному квадрату.)

41.  Постройте график импульса, описываемого выражением

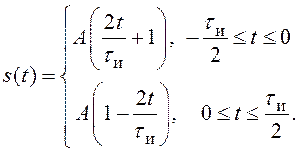 Определите спектральную плотность, постройте её график. Найдите спектр периодической последовательности таких импульсов с периодом повторения, равным .  

42.  Постройте график импульса, описываемого выражением

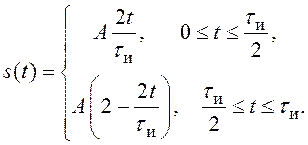 Определите спектральную плотность.

43.  Найдите сигнал, который имеет спектральную плотность

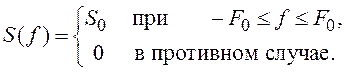 Постройте график.

44.  Постройте график «пачки» импульсов прямоугольной формы, описываемой выражением

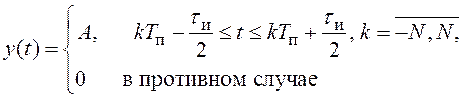
при . Определите спектральную плотность при произвольном целом .

45.  Найдите спектр относительно базиса 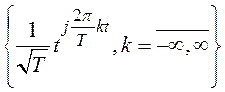 следующих сигналов из :

а)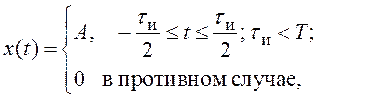

б)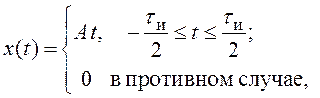

в)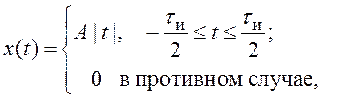

г)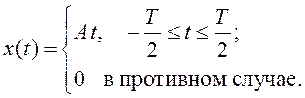

46.  Найдите минимальную частоту дискретизации сигнала со спектральной плотностью 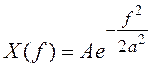 так, чтобы энергия ошибки восстановления сигнала по отсчетам не превосходила 5% от энергии сигнала.

47.  Применение противоподменного фильтра нижних частот, ограничивающего ширину спектра сигнала до дискретизации, позволяет уменьшить энергию ошибки восстановления вдвое. Определите частоту дискретизации для условий предыдущей задачи при использовании противоподменного ФНЧ. 

3. СЛУЧАЙНЫЕ ПРОЦЕССЫ

1.  По каналу связи с помехами передается одна из двух кодовых комбинаций 11111 или 00000 с вероятностями соответственно 0,6 и 0,4. Из-за помех в канале каждый символ (1 или 0) может быть принят за другой с вероятностью 0,7 независимо от соседних символов. В приемном устройстве принята комбинация 01011. Определите вероятность того, что была передана комбинация 11111.

2.  Отсчет  случайного процесса  в некоторый момент времени представляет собой случайную величину с плотностью распределения вероятностей (ПРВ) . Случайная величина  представляет собой сумму  и неслучайной постоянной . Определите вид ПРВ .

3.  Случайный аналоговый сигнал с нормальным распределением, имеющим математическое ожидание  и СКО , подвергается квантованию на 3 уровня при помощи квантователя с характеристикой, показанной на Рис. 6. Найдите вероятности значений    квантованного сигнала при , , ; при , , .

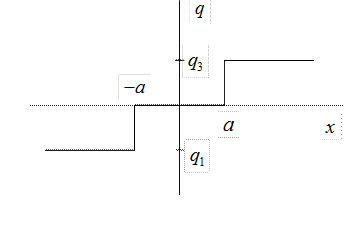
Рис. 6

4.  Реализации случайного процесса представляют собой функции времени ,  при некотором фиксированном значении  и случайной начальной фазе , имеющей распределение, равномерное в интервале . Найдите плотность распределения вероятностей мгновенного значения этого процесса.

5.  Мгновенное значение случайного процесса имеет распределение вероятностей с плотностью вида . Найдите константу , математическое ожидание и дисперсию. Постройте графики плотности распределения вероятностей и функции распределения вероятностей (друг под другом в одном масштабе).