а) ![]() ,
причем
,
причем ![]() , только если
, только если ![]() ;
;
б) ![]() (неравенство
треугольника);
(неравенство
треугольника);
в) ![]() .
.
Пусть
![]() – линейное пространство над полем
– линейное пространство над полем ![]() (или
(или ![]() ).
Функция (функционал)
).
Функция (функционал) ![]() называется скалярным
произведением, если она удовлетворяет следующим условиям:
называется скалярным
произведением, если она удовлетворяет следующим условиям:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ,
причем
,
причем ![]() , только если
, только если ![]() .
.
В пространстве со скалярным произведением выполняется неравенство Шварца
![]() или
или ![]() ,
,
на основе которого может быть введено понятие угла ![]() между векторами (только для
пространства над полем
между векторами (только для
пространства над полем ![]() ), такого что
), такого что
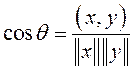 .
.
Совокупность
векторов линейного пространства ![]() является линейно независимой,
когда
является линейно независимой,
когда 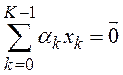 в том и только в том случае, если
в том и только в том случае, если ![]() при всех
при всех ![]() (здесь
(здесь
![]() – количество векторов).
– количество векторов).
Если
в пространстве ![]() можно найти
можно найти ![]() линейно независимых элементов, а любые
линейно независимых элементов, а любые ![]() элементов этого пространства линейно
зависимы, то пространство
элементов этого пространства линейно
зависимы, то пространство ![]() имеет размерность
имеет размерность ![]() . Если в
. Если в ![]() можно
указать систему из произвольного конечного числа линейно независимых
векторов, то говорят, что пространство
можно
указать систему из произвольного конечного числа линейно независимых
векторов, то говорят, что пространство ![]() бесконечномерно.
бесконечномерно.
Базисом
![]() -мерного пространства
-мерного пространства ![]() называется любая система из
называется любая система из ![]() линейно независимых векторов. Базисом
бесконечномерного пространства является бесконечная совокупность векторов,
такая, что любое ее конечное подмножество линейно независимо. Базис
бесконечномерного пространства полон, если в пространстве не существует
векторов, ортогональных всем векторам базиса.
линейно независимых векторов. Базисом
бесконечномерного пространства является бесконечная совокупность векторов,
такая, что любое ее конечное подмножество линейно независимо. Базис
бесконечномерного пространства полон, если в пространстве не существует
векторов, ортогональных всем векторам базиса.
2. Прямое и обратное ![]() -преобразование
-преобразование
Прямое ![]() -преобразование последовательности
-преобразование последовательности ![]() определяется выражением
определяется выражением
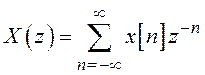 .
.
Обратное ![]() -преобразование
-преобразование
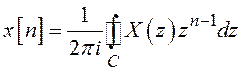 ,
,
где
![]() – контур, расположенный в области
сходимости и охватывающий начало координат, направление обхода контура – против
часовой стрелки.
– контур, расположенный в области
сходимости и охватывающий начало координат, направление обхода контура – против
часовой стрелки.
Теорема о вычетах:
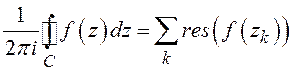 ,
,
где
![]() – изолированные полюсы, находящиеся внутри
контура интегрирования. Если
– изолированные полюсы, находящиеся внутри
контура интегрирования. Если ![]() – полюс порядка
– полюс порядка ![]() , то
, то
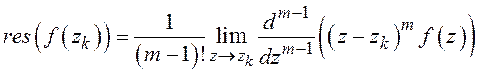 .
.
3. Прямое и обратное преобразование Фурье для последовательностей
Прямое преобразование Фурье для последовательностей определяется выражением
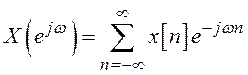 .
.
Для абсолютно
суммируемой последовательности ![]() ряд в правой части
выражения сходится равномерно к непрерывной функции аргумента
ряд в правой части
выражения сходится равномерно к непрерывной функции аргумента ![]() .
.
Обратное преобразование Фурье для последовательностей определяется выражением
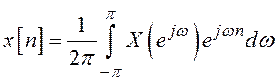 ,
, ![]() .
.
4. Формулы Эйлера
![]() ,
,
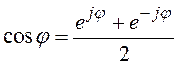 ,
,
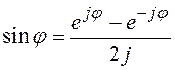 .
.
5. Геометрическая прогрессия
Сумма геометрической прогрессии
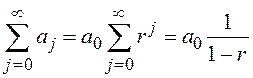 ,
при
,
при ![]() ,
,
где ![]() ,
, ![]() ,
, ![]() – первый член,
– первый член, ![]() – знаменатель прогрессии.
– знаменатель прогрессии.
Частичная сумма геометрической прогрессии 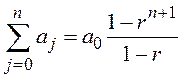 .
.
6. Некоторые тригонометрические соотношения
![]() ,
,
![]() ,
,
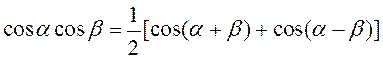 ,
,
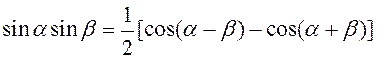 ,
,
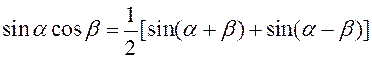 ,
,
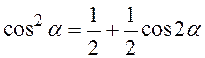 ,
, 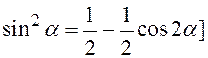 ,
,
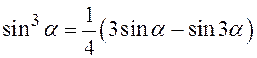 ,
, 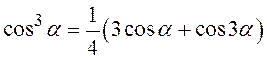 .
.
7. Некоторые производные
![]() ,
, 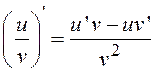 ,
, 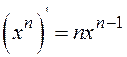 ,
, 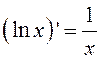 ,
,
![]() ,
, ![]() ,
, 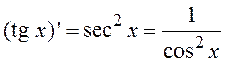 ,
,
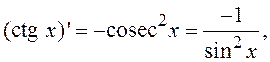
![]()
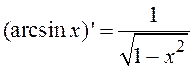 ,
, 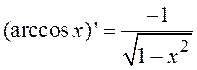 ,
, 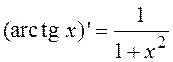 ,
, 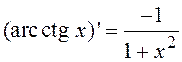 ,
,
![]() ,
, ![]() .
.
8. Некоторые интегралы
Неопределенные интегралы
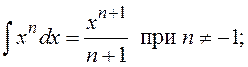
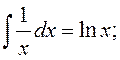
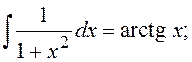
![]()
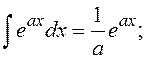
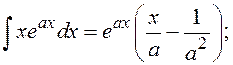
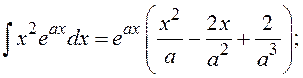
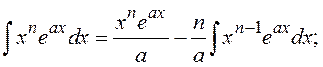
Определенные интегралы
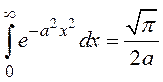 ,
,![]() ,
,
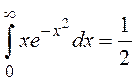 ,
, 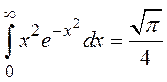 ,
,
Интегрирование по частям
![]() или
или 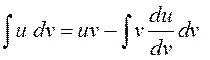 .
.
Интегрирование приведением к полному квадрату
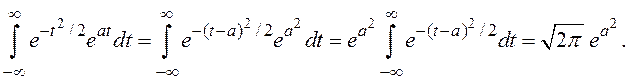
9. Интеграл вероятностей
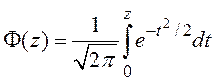
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.