8. Постройте графики сигнала ![]() при
при
а) 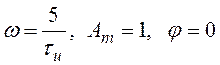 ;
;
б) 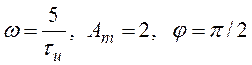 ;
;
в)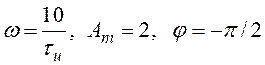 ,
,
если ![]() .
.
9. Экспоненциальный импульс задан выражением
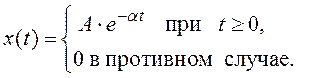
![]()
Определите эффективную длительность импульса, как длину интервала, на котором сосредоточено 90% энергии сигнала.
10.
Определите
эффективную длительность биэкспоненциального импульса ![]() как
длину интервала, на котором сосредоточено 95% энергии сигнала (
как
длину интервала, на котором сосредоточено 95% энергии сигнала (![]() ).
).
11. Колокольный (гауссовский) импульс
определяется выражением 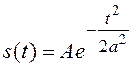 . Найдите эффективную
длительность по энергетическому критерию при
. Найдите эффективную
длительность по энергетическому критерию при ![]() .
.
12. Постройте графики вещественной и
мнимой частей комплексного колебания ![]() .
.
13. Постройте векторные диаграммы для колебания
![]() для
для ![]() .
.
14. Постройте векторные диаграммы для колебания
![]()
для ![]() .
.
15. Проверьте, образует ли множество
действительных чисел ![]() группу относительно операции
сложения; относительно операции умножения.
группу относительно операции
сложения; относительно операции умножения.
16. Пусть ![]() –
множество всех четных целых чисел. Образует ли множество
–
множество всех четных целых чисел. Образует ли множество ![]() группу относительно операции сложения?
относительно операции умножения?
группу относительно операции сложения?
относительно операции умножения?
17. Найдите нормы (в ![]() ) сигналов
) сигналов
а) ![]() ,
,
б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)
, д) ![]() .
.
18. Найдите скалярные произведения пар сигналов, упомянутых в предыдущей задаче: а) и б); в) и г); б) и д); а) и г).
19. Найдите расстояния между сигналами в этих же парах в евклидовой метрике.
20. Найдите углы между сигналами ![]() , как векторами в гильбертовом
пространстве
, как векторами в гильбертовом
пространстве ![]() при
при ![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
Постройте на основе этой совокупности функций ортонормальный базис. Охарактеризуйте пространство сигналов, натянутое на этот базис.
Смените нумерацию сигналов на обратную и постройте ортонормальный базис. Сравните результаты.
21. Найдите угол между сигналами ![]() и
и ![]() , как
векторами гильбертова пространства, если
, как
векторами гильбертова пространства, если ![]() ; если
; если ![]()
![]()
![]() .
.
22. Найдите скалярные произведения сигналов
а) ![]() и
и ![]() при
при ![]() ;
;
б) ![]() и
и ![]() .
.
23. Прямоугольные функции Радемахера при ![]() описываются выражением
описываются выражением 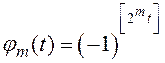 , где
, где ![]() –
номер функции, а квадратные скобки обозначают целую часть числа, заключенного в
них. Постройте графики первых 8 функций. Проверьте ортонормальность системы
функций Радемахера. Убедитесь в том, что функция
–
номер функции, а квадратные скобки обозначают целую часть числа, заключенного в
них. Постройте графики первых 8 функций. Проверьте ортонормальность системы
функций Радемахера. Убедитесь в том, что функция ![]() ортогональна
всем функциям
ортогональна
всем функциям ![]() ,
, ![]() (что
говорит о неполноте системы Радемахера в качестве базиса пространства
(что
говорит о неполноте системы Радемахера в качестве базиса пространства ![]() ).
).
24. На основе системы функций Радемахера
постройте графики новых функций ![]() , воспользовавшись формулой
, воспользовавшись формулой
![]() при
при ![]() .
.
25. Постройте графики 8 первых функций
Уолша ![]() ,
, ![]() ,
пользуясь выражением
,
пользуясь выражением ![]() , где
, где
![]() ,
, ![]()
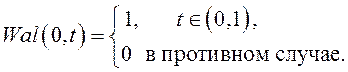 Убедитесь, что функции
Убедитесь, что функции ![]() , построенные в предыдущей задаче, являются
функциями Уолша.
, построенные в предыдущей задаче, являются
функциями Уолша.
26. Найдите первые 8 коэффициентов разложения импульса, показанного на Рис. 3, в базисах Радемахера и Уолша. Постройте графики соответствующих аппроксимаций импульса.
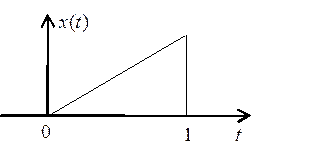
Рис. 3
27. Найдите первые 8 коэффициентов разложения импульса, показанного на Рис. 4, в базисе Уолша.
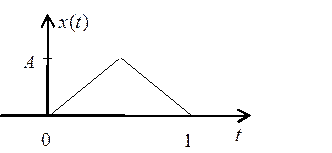
Рис. 4
Постройте график аппроксимации импульса.
28. Функции Хаара, образующие
ортонормальный полный базис пространства ![]() ,
определяются следующими выражениями:
,
определяются следующими выражениями: ![]()
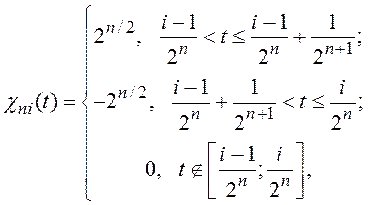 при
при ![]() и
и ![]() .
.
Постройте графики функций ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Постройте аппроксимацию треугольного импульса (Рис. 4) суммой этих функций.
29.
Чётный
прямоугольный импульс единичной амплитуды, заданный на интервале (–1;1) и
имеющий длительность 0,5 с, аппроксимируется конечной суммой комплексного ряда
Фурье. Определите норму ошибки аппроксимации, если количество слагаемых ![]() .
.
30. Найдите скалярное произведение пары функций из набора
![]()
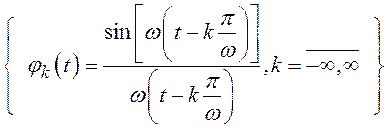
при одинаковых индексах; при разных индексах .
31. Найдите импульсную характеристику цепи с КЧХ вида
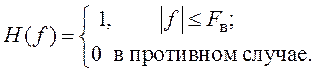
![]()
32. Найдите импульсную характеристику цепи с КЧХ вида
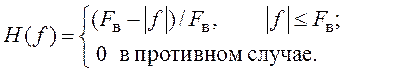
![]()
33.
Определите
колебание, сопряженное по Гильберту , по отношению к ![]() к
к
![]() к
к ![]() .
.
34. На множестве, состоящем из чисел 0 и 1, приведенными ниже таблицами определены операции сложения и умножения.
Таблица сложения Таблица умножения
|
+ |
0 |
1 |
´ |
0 |
1 |
||
|
0 |
0 |
1 |
0 |
0 |
0 |
||
|
1 |
1 |
0 |
1 |
0 |
1 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.