Теория электрической связи: Сборник задач и упражнений, страница 7

-  безошибочного приема;

-  того, что в блоке из  символов будет ошибочно принят хотя бы один символ;

-  того, что в блоке из  символов будет  и более ошибок.

8. ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ

1.  На входе дискретного канала без памяти действует источник без памяти с алфавитом, содержащим три символа , , . На выходе канала вырабатываются символы , , . Совместные вероятности пар символов определяются таблицей

Определите все условные вероятности вида  и . Найдите безусловные вероятности символов  и  для всех  и .

2.  Даны два дискретных источника  и   с алфавитами, содержащими по три символа (, ,  и , ,  соответственно). Заданы все совместные вероятности :

    Проверьте, являются ли источники независимыми.

3.  На входе канала связи действует двоичный дискретный источник информации  с алфавитом , вероятности символов равны  и . При передаче символа 0 по каналу ошибка происходят с условной вероятностью , а при передаче символа 1 – с вероятностью . Считая выход канала источником , рассчитайте ненадежность, как условную энтропию .

4.  В цифровой системе передачи данных используются два сигнала, которым соответствуют два символа, условно обозначаемые “0” и “1”. Вероятности появления символов на выходе источника сообщений равны соответственно  и . Постройте график зависимости энтропии источника (без памяти) от вероятности .

5.  В цифровой системе черно-белого телевидения сообщением является полутоновое изображение, состоящее из точек (пикселов), яркость которых может принимать одно из 256 значений. Определите количество информации, содержащееся в одном изображении размерами 625×833, если значения яркостей отдельных пикселов представляют собой независимые случайные величины, имеющие равновероятное распределение.

6.  Сообщение об исходе опыта – например, о номере шара, извлеченного наугад из урны с  шарами (все шары пронумерованы от 1 до , шаров с одинаковыми номерами в урне нет, все исходы равновероятны) передано по каналу связи  в виде слова 00101111. Переданное сообщение  полностью сняло неопределенность относительно исхода опыта. Сколько вопросов с ответами типа “да”, “нет” нужно было бы задать, чтобы полностью снять неопределенность относительно исхода этого опыта? Какое количество информации несет данное сообщение? Сколько шаров в урне?

7.  На входе двоичного дискретного однородного симметричного канала со стиранием действует источник без памяти с алфавитом, состоящим из символов  и , передаваемых с равными вероятностями. На выходе канала вырабатываются символы , , совпадающие соответственно с  и , и символ стирания , означающий отказ приемника от принятия решения в пользу  или . Имеют место следующие условные (переходные) вероятности

;

.

Найдите апостериорные вероятности передачи  символов  и  при приеме  и , безусловную вероятность ошибочного приема и безусловную вероятность стирания [4].

8.  Двоичный стационарный источник без памяти вырабатывает символы  и  с вероятностями 0,05 и 0,95 соответственно. Постройте коды Шеннона–Фано  и Хаффмена для случаев кодирования пар и троек символов. Определите избыточность получаемых кодов.

9.  Проверьте, является ли матрица

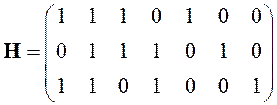
проверочной для кодовой матрицы

.

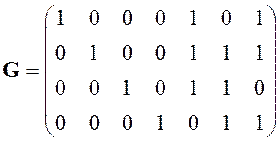10.  Найдите хэммингово расстояние между всевозможными парами строк порождающей матрицы (7,4)-кода Хэмминга. 

9. ОСНОВЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ

1.  На выходе аналогового канала связи наблюдается колебание , представляющее собой либо шум  (гипотеза ), либо сумму сигнала  с шумом (гипотеза ). Считая шум гауссовским с нулевым средним и среднеквадратическим отклонением (СКО) , а сигнал – прямоугольным видеоимпульсом амплитуды , запишите выражения плотности вероятности мгновенного значения  смеси  для обеих гипотез.