Теория электрической связи: Сборник задач и упражнений, страница 4

6.  Мгновенное значение случайного процесса описывается функцией распределения . Найдите плотность распределения вероятностей, математическое ожидание, дисперсию. Постройте графики плотности распределения вероятностей и функции распределения вероятностей (друг под другом в одном масштабе).

7.  Функция автокорреляции стационарного случайного процесса имеет вид , где  – некоторая постоянная. Найдите спектральную плотность мощности случайного процесса. Постройте графики.

8.  Спектральная плотность мощности стационарного случайного процесса  имеет вид , где  и  – некоторые постоянные. Найдите автокорреляционную функцию процесса. Постройте графики.

9.  Определите функцию распределения вероятностей и моменты 1 и 2 порядков случайной величины с плотностью

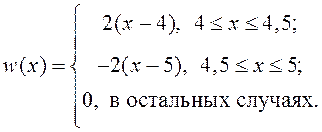
10.  Определите функцию распределения вероятностей, моменты 1 и 2 порядков и связь между величинами  и  по заданной ПРВ случайной величины

 а)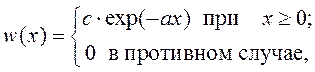

 б).

11.  Определите характеристическую функцию случайной величины с равномерным распределением вероятностей с плотностью

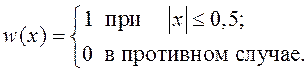
12.   Определите функцию распределения вероятностей, моменты 1 и 2 порядков и связь между величинами ,  и  для случайной величины с ПРВ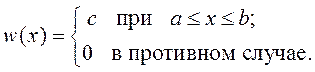

13.  Определите ПРВ и моменты 1 и 2 порядков случайных величин с функциями распределения

 а)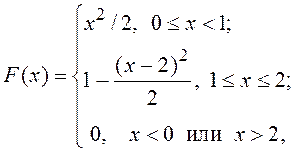

 б)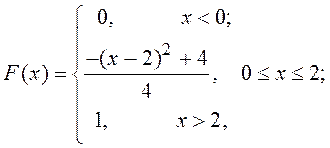

 в)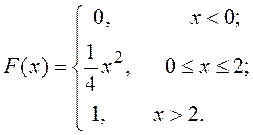 

14.  Определите, является ли стационарным и (или) эргодическим процесс, все реализации которого представляют собой функции  при , где  – случайная величина с равномерным на  распределением.

15.  Найдите ПРВ тока, протекающего через безынерционный нелинейный элемент с вольтамперной характеристикой 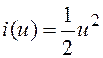, если к нему приложено шумовое напряжение с ПРВ

  

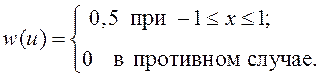
16.  Найдите ПРВ мгновенного значения случайного процесса на выходе безынерционного нелинейного звена с характеристикой , если на входе действует случайный процесс с ПРВ мгновенного значения

 

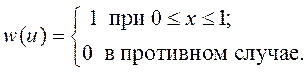
17.  Найдите ПРВ мгновенного значения случайного процесса на выходе безынерционного нелинейного звена с характеристикой , если на входе действует случайный процесс с ПРВ мгновенного значения

 

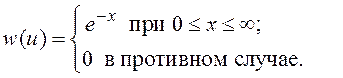
18.   Изобразите примерный вид плотности распределения вероятности случайного процесса, реализации которого имеют вид последовательностей импульсов с одинаковой амплитудой и случайной длительностью,    Рис. 7.

Рис. 7

19.   Изобразите примерный вид плотности распределения вероятности случайного процесса, реализации которого имеют вид прямоугольных колебаний с постоянной амплитудой и случайной сменой полярности, Рис. 8  

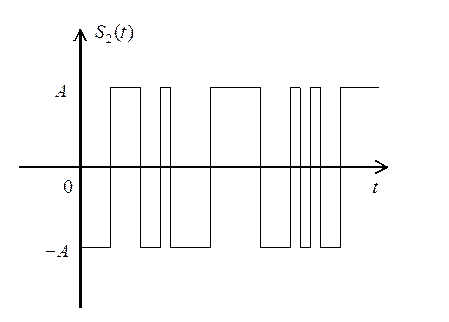
Рис. 8

20.  Для сигналов, показанных на Рис. 9 и Рис. 10, изобразите примерный вид плотности распределения вероятности.

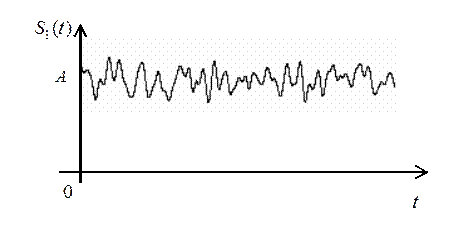
Рис. 9

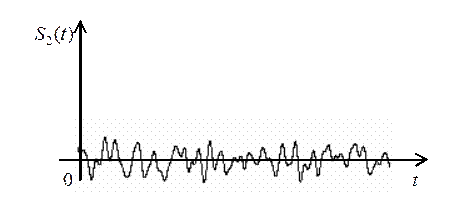
    Рис. 10

21.  Определите математическое ожидание, дисперсию и функцию распределения вероятностей случайного напряжения, имеющего плотность распределения, показанную на Рис. 11, а – е.

22.  Случайный сигнал имеет математическое ожидание 2 В и дисперсию, равную 9 В². Шум в канале связи гауссовский с нулевым средним и дисперсией 0,09 В². Сигнал и шум независимы. Определите математическое ожидание и дисперсию аддитивной смеси сигнала с шумом. Каким было бы математическое ожидание выходного сигнала при мультипликативном взаимодействии?

Рис. 11

4. МЕТОДЫ АНАЛИЗА ЛИС-ЦЕПЕЙ

1.  Комплексная частотная характеристика (КЧХ) цепи  может быть найдена как отношение выходного и входного сигналов, но только в том случае, если входным сигналом является комплексное гармоническое колебание . Найдите КЧХ цепей, показанных на Рис. 12.

         

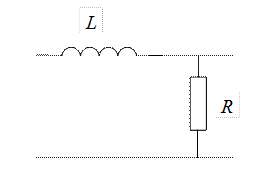
Рис. 12

2.  Найдите импульсные характеристики цепей, показанных на Рис. 12, через преобразование Фурье.

3.  Найдите КЧХ последовательного контура, показанного на Рис. 13, а затем импульсную характеристику.

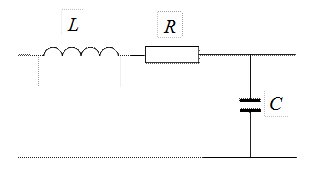
Рис. 13

4.  Составьте дифференциальное уравнение -фильтра нижних частот (интегрирующей цепочки). Выведите КЧХ и передаточную функцию цепи. Найдите импульсную характеристику.