Статистическое моделирование экономических показателей, страница 6

Табличное значение критерия Груббса составляет 2,17. Рассчитанные значения  критерия Груббса из таблицы 7 не превышают данного показателя, следовательно, выборочные значения не содержат аномальных наблюдений. 

2.2 Проверка на нормальность распределения

Проверка на нормальность распределения предусматривает проверку следующей системы неравенств:

,

Где  ,  - средние квадратичные ошибки асимметрии и эксцесса, определяемые следующим образом:

,

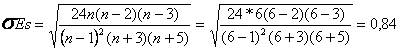
Подставив полученные значения в систему неравенств, получим следующие данные:                           

                         

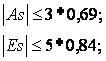
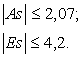
По результатам расчётов неравенства выглядят следующим образом:

- для Y:

- для Х1: ;

- для Х2:

- для Х3:

Следовательно, по предварительным расчётам можно сделать вывод, что изучаемые ряды подчиняются нормальному закону распределения.

Для уточнения результатов необходимо провести проверку по критериям К. Пирсона, В.И. Романовского и А.Н. Колмогорова. Основные этапы соответствующего алгоритма и результаты расчётов можно интерпретировать следующим образом.

Этап 1.Определение количества интервалов, на которые разбивается выборка в 7 наблюдений.

Этап 2. Расчёт шага интервала

В таблице 7 приведены исходные данные и итоги расчётов вышеперечисленных этапов для результативного показателя Y.

  Таблица 8

Среднее квадратичное отклонение	0,841	Среднее значение	0,566	Количество интервалов	3,585
Максимальное значение	1,499	Минимальное значение	-0,219	Шаг интервала	0,430

Этап 3. Формирование границ интервалов (t_j^в – верхняя граница интервала, t_j^н - нижняя).

Этап 4. Определение нормированных отклонений от верхних и нижних границ интервалов (t_j^в’, t_j^н’)

Этап 5. Определение эмпирических частот (f_j)

Итоги расчётов вышеперечисленных трёх этапов для результативного показателя представлены в таблице 9.

Таблица 9

tн	tв	t'н	t'в	F(t'н)	F(t'в)
-0,219	0,211	-0,933	-0,423	0,175	0,336
0,211	0,641	-0,422	0,089	0,336	0,535
0,641	1,071	0,089	0,600	0,536	0,726
1,071	1,501	0,600	1,111	0,726	0,867