В данном разделе представлены графики полей корреляции, отражающие зависимость между результативным показателем и факторными признаками, а также изображены эллипсы рассеяния, позволяющие сделать предварительные выводы о наличии и характере стохастической зависимости.
На рис. 2.1, 2.2, 2.3 приведены соответствующие графики по данным таблицы 1.
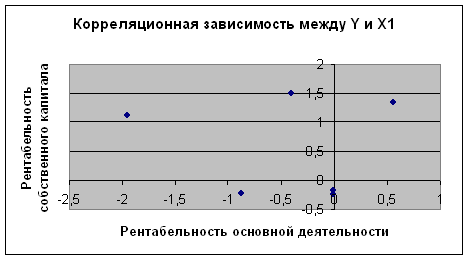
Рис. 2.1 Корреляционная зависимость между Y и X1
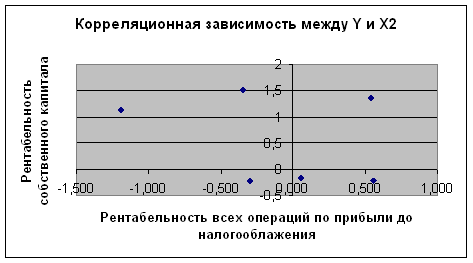
Рис. 2.2 Корреляционная зависимость между Y и X2
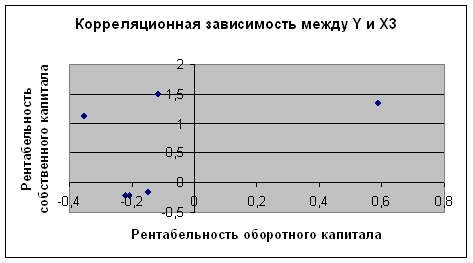
Рис. 2.3 Корреляционная зависимость между Y и X3
Характер расположения точек корреляционных полей позволяет сделать предварительный вывод об отсутствии линейной зависимости между факторными признаками и результативным показателем. Проверку значимости парных коэффициентов корреляции для обоснования выбора фактора, оказывающего наиболее существенное влияние на изменение результативного признака лучше осуществлять аналитическим способом, более точного по сравнению с графическим.
Значимость линейного парного
коэффициента корреляции, т.е. гипотеза об отсутствии в генеральной совокупности
наблюдений линейной корреляционной зависимости, проверенная по t–критерию Стьюдента 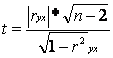 , представлена в таблице 20 .
, представлена в таблице 20 .
Таблица 20 Расчётные значения критерия Стьюдента
|
X1 |
0,182 |
|
X2 |
0,610 |
|
X3 |
0,938 |
Расчётные значения данного критерия не превышают табличное, равное 4,604 при уровне значимости 1% и числе степеней свободы 4 (f = 6-2). Следовательно, гипотеза об отсутствии в генеральной совокупности наблюдений линейной корреляционной зависимости принимается, т.е. выводы считаются незначимыми. В данном случае зависимыми от объёма выборки.
2.4 Регрессионный анализ показателей
Рентабельность оборотного капитала (X3) оказывает наиболее сильное влияние на изменение результативного показателя, так как ему соответствует максимальное по абсолютной величине значение парного коэффициента корреляции.
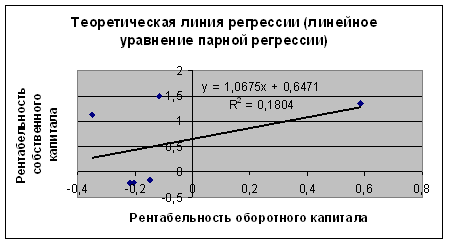
Рис. 2.4
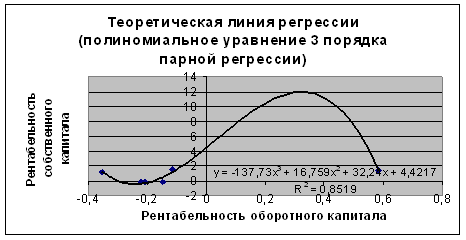
Рис. 2.5
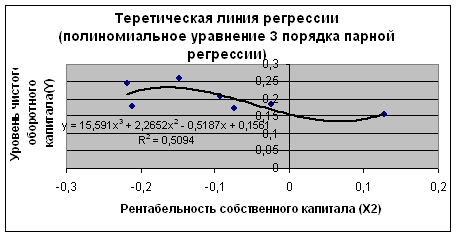
Рис. 2.6
Из множества построенных уравнений регрессии уравнения полиномиальное 2 и 3 порядка уравнение парной регрессии являются наиболее качественными по критерию максимума достоверности аппроксимации R2 .
Значимость уравнения определяется возможностью надёжного прогноза результативного показателя по значениям факторных признаков. Поэтому важным этапом является проверка значимости уравнения регрессии по критерию Фишера.
Для выбора лучшего уравнения регрессии (из множества значимых) могут быть использованы следующие критерии их качества:
- минимум остаточной дисперсии;
- минимум корреляционного отношения:
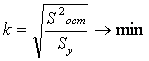 ;
;
- минимум относительной ошибки аппроксимации:
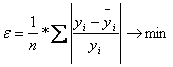
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.