Другие предметы \ Экономико-математическое моделирование

Статистическое моделирование экономических показателей, страница 17

Сравнивая табличное значение критерия Фишера 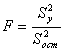 (при уровне значимости 5% составляющее 4,21) с расчётными критериями, можно сделать вывод о том, что в этом  уравнении не принимается выдвинутая гипотеза о значимости уравнений регрессии, так как расчётные значения критерия больше табличного.

В таблице 24 представлены значения всех критериев оценки качества построенных уравнений и результаты их ранжирования.

Таблица 24

Y=1,0675*X+0,6471

Y=3,3041*X^2+0,0127*X+0,2397

Y=-137,73*X^3+16,759*X^2+32,24*X+4,4217

E

1,937

3

1,657

2

0,929

1

k

0,905

3

0,866

2

0,385

1

S 2 ост

0,579

3

0,530

2

0,105

1

Таким образом, можно сделать вывод, что лучшим уравнением является 3 (полиномиальное уравнение 3 порядка), так как ему соответствует наименьшее суммарное количество баллов. Кроме парного, целесообразно также провести множественный регрессионный анализ, построив линейное уравнение множественной регрессии и оценив его значимость.

Таблица 25

2,033752547

-1,7527

0,5943

0,78937

1,500367542

1,61382

1,3789

0,50152

0,686728594

0,74383

#Н/Д

#Н/Д

1,4614135

2

#Н/Д

#Н/Д

2,425703141

1,10656

#Н/Д

#Н/Д
Скачать файл