Статистическое моделирование экономических показателей, страница 11

Расчётное значение критерия К. Пирсона для результативного показателя (Х2) составляет:

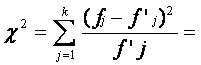0,782.

         Этот коэффициент  превышает табличные значения при числе степеней свободы 1 (f = k – 3 = 4 - 1) независимо от уровня доверительной вероятности. Следовательно, расхождение между теоретическими и эмпирическими частотами существенно и его нельзя объяснить колебаниями выборочных данных, т.е. гипотеза о близости эмпирического распределения нормальному отвергается. 

         Значение критерия В.И. Романовского составляет:

.

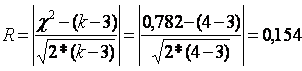         Данная величина не превышает значения 3, следовательно, выдвинутая гипотеза не принимается.

         Критерий А.Н. Колмогорова равен:

;

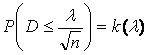         где D = max 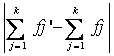= 2,033.

         Выполнение условия по критерию Колмогорова (2,033 > 2/) при уровне доверительной вероятности 0,9993 позволяет сделать вывод, что исследуемое распределение подчиняется нормальному закону распределения.

Расчёт критериев согласия и проверка выдвинутой гипотезы о соответствии эмпирического распределения теоретическому для Х3:

Таблица 17

 Таблица 18