Ядерный магнитный резонанс (Лабораторная работа 2.3), страница 4

Современная квантовая теория нуклонов и атомных ядер не завершена, поэтому ядерные факторы находят экспериментально. Именно фактор является индивидуальной характеристикой ядра. Значения  и  для некоторых изотопов приведены в Таблице 2. 2.

            Энергия магнитного момента в магнитном поле  лишь постоянным множителем отличается от энергии волчка в поле тяжести  ( - масса волчка,  - высота центра тяжести над точкой опоры). Поэтому движение намагниченного волчка полностью подобно движению быстрого симметричного волчка в поле тяжести. В постоянном магнитном поле вектор магнитного момента будет прецессировать вокруг направления вектора Н₀ с постоянной угловой скоростью  независимо от направления вектора , т.е. от угла между осью вращения частицы и направлением поля (рис.1.2). Угловую скоростью такой прецессии называют ларморовской частотой.

            Уравнение движения

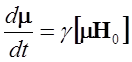                       (1.5)

можно получить, если приравнять скорость изменения момента импульса моменту сил, действующих на волчок. Обратим внимание, что величина и направление магнитного поля могут быть переменными. Тогда и угловая скорость прецессии окажется переменной.

Если перейти к системе координат, вращающейся равномерно с угловой скоростью w, то можно показать, что уравнение движения магнитного момента (1.5) остается справедливым, если заменить магнитное поле Н₀на

Вектор угловой скорости вращения . Знак минус появляется потому, что вращение происходит в левую сторону. В частности, при  имеем , т.е в системе координат, вращающейся относительно Н₀ с ларморовской частотой магнитный момент неподвижен.

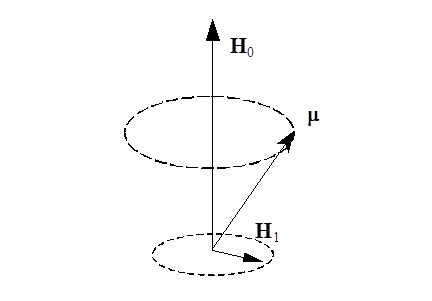
Рис.1.2. Прецессия магнитного момента в магнитном поле Н₀

Допустим теперь, что кроме поля Н₀ введено другое, более слабое поле Н₁<<H₀, постоянное по величине и равномерно вращающееся в плоскости, перпендикулярной направлению Н₀ (рис.1.2, 1.3) с частотой . Пусть, для определенности, во вращающейся системе координат Н₀ ориентировано по оси z, а Н₁ – по оси x[2]. Тогда в системе координат, вращающейся с частотой , на магнитный момент действует эффективное поле

.

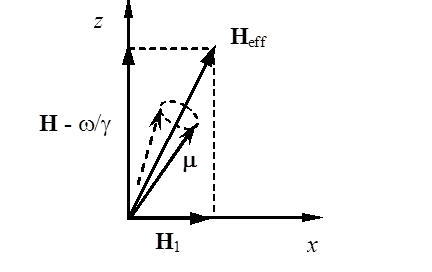
Рис. 1.3. Прецессия магнитного моменте в системе координат, вращающейся с частотой .

Вектор  прецессирует во вращающейся системе координат вокруг . Такое движение принято называть нутацией или осцилляциями Тори. Частота прецессии равна , где .

При  вектор  прецессирует вокруг оси х. В этом случае амплитуда изменения проекции , а, следовательно, и энергии ядра в магнитном поле принимает максимальное значение. В неподвижной (лабораторной) системе координат медленное движение  вокруг Н₁ дополняется более быстрым прецессионным движением вокруг Н₀ (рис. 1.4).

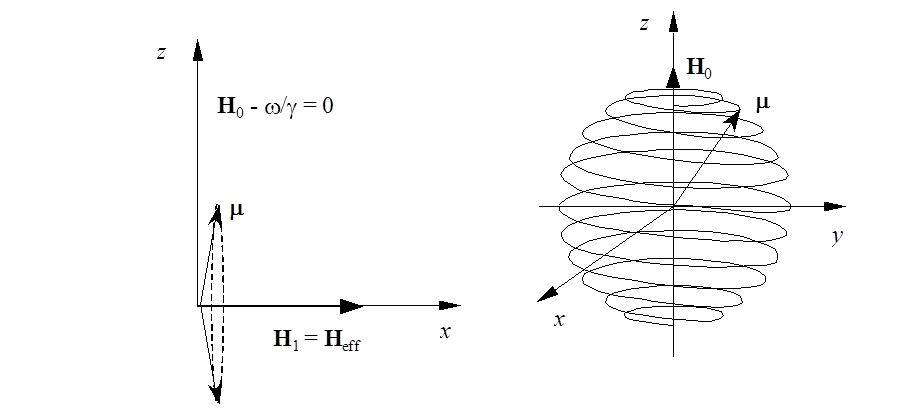
Рис. 1.4. Слева – прецессия магнитного момента  в системе координат, вращающейся с резонансной частотой . Справа – приблизительное движение  в лабораторной системе координат.

Амплитуда осцилляций быстро затухает с изменением , стремясь к нулю при . Это и есть резонанс с точки зрения классического движения вектора намагниченности. Ширина резонанса определяется соотношением .

Частота прецессии  относительно Н₁ при резонансе равна . Угол поворота  относительно Н₁ при включении импульса переменного поля длительностью  есть

.                                                                        (1.6)

Эта формула имеет важное значение для импульсных методов в магнитном резонансе.

Движение магнитного момента с учетом релаксации описывается при помощи уравнений Блоха. Сравнение выводов, полученных на основе решения уравнений Блоха, с экспериментальными результатами, показывает, что они достаточно хорошо описывают явления, происходящие в жидких образцах.

Некоторые вопросы импульсного ЯМР