Ядерный магнитный резонанс (Лабораторная работа 2.3), страница 2

В соответствии с представлениями квантовой теории ориентации ядерного спина квантованы, т.е. компонента m_I вектора ядерного спина в любом заданном направлении может принимать только одно из значений +I, +(I-1), …, -I. Величину m_I называют ядерным спиновым квантовым числом. Для протона I = ½ и m_I может быть равно +1/2 или –1/2 . Если протон поместить в постоянное магнитное поле H, то возникает взаимодействие между магнитным моментом μ_N протона и полем H, энергия взаимодействия равнва . Если магнитное поле направлено вдоль оси z, то , где I_z – проекция ядерного спина протона на ось z, имеющая значения +1/2 или –1/2. На рисунке 1.1 приведена схема энергетических уровней протона в постоянном магнитном поле. Поскольку ядерный магнетон b_N является положительной величиной и g_N-фактор для протона также положителен, то состоянию с меньшей энергией соответствует значение m_I = + 1/2, т.е. в данном состоянии ядерный момент параллелен магнитному полю H. В состоянии с большей энергией направление поля и проекция ядерного спина антипараллельны. Обычно состояние с m_I = + 1/2, обозначают символом , а состояние с m_I = - 1/2 символом . Энергии этих состояний равны .

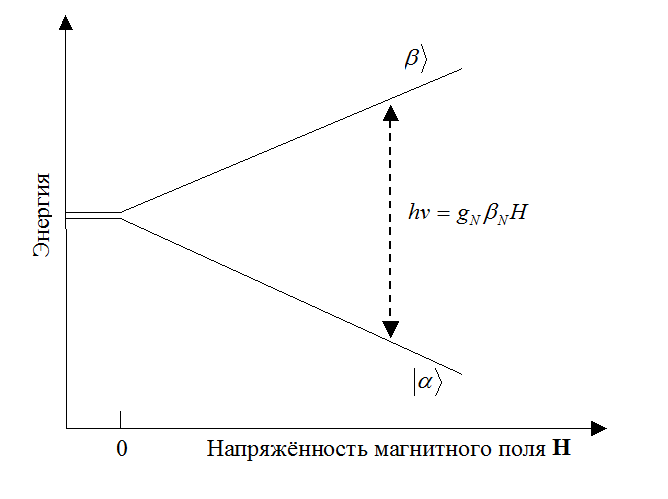
Рис.1.1.Схема энергетических уровней ядра атома в магнитном поле.

Произвольное нестационарное состояние имеет вид , где постоянные  и  связаны условием нормировки  и поэтому могут быть выбраны в виде

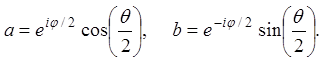                             (1.2)

Такому выбору отвечает направление спина, заданное сферическими углами . Зависимость сферической функции от времени

сводится, как легко видеть, к замене в (1.2)  на  где . Это означает, что спин вращается вокруг оси  с угловой скоростью , а угол его наклона не меняется. Такое движение называют прецессией.

В макроскопическом ансамбле протонов, помещённых в магнитное поле H, одна часть протонов находится в состоянии , другая – в состоянии . Распределение спинов между двумя возможными состояниями подчиняется закону Больцмана, согласно которому 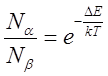, где N_α – число спинов в состоянии , N_β – число спинов в состоянии , а ΔЕ – разность энергий, равная . Среднее значение магнитного момента равно

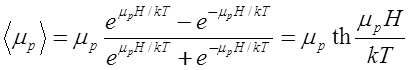
В условиях, типичных для ЯМР,  так что  - величина  очень мала. Тем не менее, именно это – исходная величина для всех работ с ЯМР.

Чтобы вызвать переходы между двумя энергетическими уровнями ядерного спина, необходимо воздействовать на систему возмущением, зависящем от времени. Так как магнитный момент взаимодействует с магнитным полем, то зависящее от времени возмущение должно быть переменным магнитным полем. Поглощение энергии происходит при условии, что магнитный вектор осциллирующего поля перпендикулярен направлению постоянного магнитного поля Н и частота ν осциллирующего поля удовлетворяет условию резонанса:

                                                                       (1.3)

Первое условие связано с квантово-механическим правилом отбора . Осциллирующее поле с равной вероятностью вызывает переходы спина из состояния  в  и из  в . Поэтому поглощение энергии будет происходить только в том случае, когда заселённость состояния  больше, чем состояния .

Уравнение (1.3) показывает, что наблюдать ядерное резонансное поглощение можно, изменяя либо магнитное поле Н, либо частоту ν. Технически более удобно проводить эксперимент при постоянной частоте, изменяя магнитное поле. Именно так и работали первые ЯМР спектрометры. С их помощью получали зависимость поглощённой энергии электромагнитного поля от величины постоянного магнитного поля. Поскольку ядерные g-фактор и спин определяются природой ядра, то для разных ядер требуются существенно разные Н и ν, чтобы выполнить условие резонанса.

Форма резонансной линии