







































Система линейных однородных уравнений с постоянными коэффициентами и её общее решение (все теоремы n-ного порядка)
Всегда их можно свести к
системе. 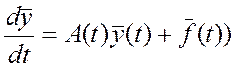 A – матрица – (aij(t)). Если
A – матрица – (aij(t)). Если ![]()
![]() однородное уравнение, если
однородное уравнение, если ![]()
![]() неоднородное.
неоднородное. 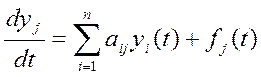 ,
, ![]() -
функция источника.
-
функция источника. ![]() - уравнение второго порядка.
Вводим:
- уравнение второго порядка.
Вводим:
![]()
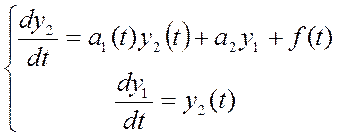
![]() линейная комбинация решений – есть решение
– для однородной системы уравнений. Если функции непрерывны
линейная комбинация решений – есть решение
– для однородной системы уравнений. Если функции непрерывны![]() условие Липшица автоматически
выполняются, то есть достаточно непрерывности (aij).
Ставится задача Коши: как находить решение:
условие Липшица автоматически
выполняются, то есть достаточно непрерывности (aij).
Ставится задача Коши: как находить решение: 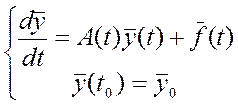 .
существует общее решение (решение однородного) и частное (решение
неоднородного) уравнений.
.
существует общее решение (решение однородного) и частное (решение
неоднородного) уравнений.
Теорема №1: любое
решение уравнения ![]() , может быть представлено в виде y(t)=
, может быть представлено в виде y(t)=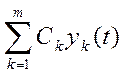 , где y1(t), y2(t),…, yn(t)
– фундаментальная система решений, Сk=const (постоянная).
, где y1(t), y2(t),…, yn(t)
– фундаментальная система решений, Сk=const (постоянная).
Доказательство:
Пусть y(t) – решение (1). Тогда берем t0![]() - некоторая точка. Положим y0=y(t0),
y01=y’(t0),…, y0(n-1)=y(n-1)(t0). У этого
уравнения есть Фундаментальная система решений. Рассмотрим систему относительно
Сk:
- некоторая точка. Положим y0=y(t0),
y01=y’(t0),…, y0(n-1)=y(n-1)(t0). У этого
уравнения есть Фундаментальная система решений. Рассмотрим систему относительно
Сk: 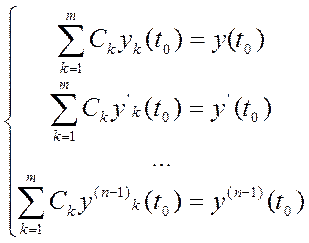 . Эта
система имеет единственное решение, так как это система фундаментальных систем
решений, а det (матрицы) = B(t0), а он
. Эта
система имеет единственное решение, так как это система фундаментальных систем
решений, а det (матрицы) = B(t0), а он ![]()
![]() по т. Крамера Сk –можно найти
по т. Крамера Сk –можно найти![]() мы знаем.
мы знаем.
Рассмотрим функцию ![]() (t)=
(t)=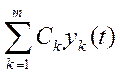 - это решение уравнения (1) ( так как
линейная комбинация). Эта функция имеет данные Коши. У
- это решение уравнения (1) ( так как
линейная комбинация). Эта функция имеет данные Коши. У ![]() (t)
совпадают данные с y(t)
(t)
совпадают данные с y(t) 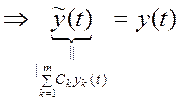 . Ч.Т.Д.
. Ч.Т.Д.
Такое решение называют общим
решением. Если уравнение неоднородное ![]() частное
решение.
частное
решение.
Простейшие методы интегрирования обыкновенных дифференциальных уравнений
Примеры дифференциальных уравнений:
1.
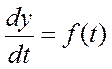 ,
, ![]() -
задана, надо найти y
-
задана, надо найти y
2.
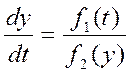 c
разделяющимися переменными ,
c
разделяющимися переменными , ![]() - функции =>
- функции =>![]() и
интегрируем.
и
интегрируем.
3.
![]() делаем замену
делаем замену ![]()
4.
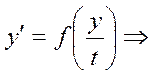 делаем замену
делаем замену 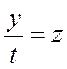
5.
![]() , где
, где ![]() и
и ![]() - две
функции. (*) Если найдется F(y,t),такое что
- две
функции. (*) Если найдется F(y,t),такое что ![]() а
а ![]()
![]() =>”первый интеграл”,
а потом ищем y как неявную функцию. (*)Если
не существует F , то домножаем на
=>”первый интеграл”,
а потом ищем y как неявную функцию. (*)Если
не существует F , то домножаем на ![]() интегрирующий множитель:
интегрирующий множитель: ![]()
6.
Уравнение
Риккати (1-ого порядка): ![]() - такое уравнение не
решается! (в квадратурах).
- такое уравнение не
решается! (в квадратурах).
7.
![]() ,
, ![]() Тогда
Тогда ![]() порядок уравнения
уменьшается на k =>
порядок уравнения
уменьшается на k => ![]() . И решаем.
. И решаем.
8.
![]() вместо
вместо ![]() => понизится
порядок.
=> понизится
порядок.![]() .
. ![]() Допустим
мы нашли p(y),
теперь надо найти исходное y
Допустим
мы нашли p(y),
теперь надо найти исходное y
9.
![]() .
F-однородна по всем переменным. Т.е.
.
F-однородна по всем переменным. Т.е.![]() .
Тогда замена
.
Тогда замена 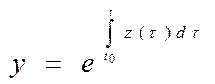 => порядок
уменьшается на один.
=> порядок
уменьшается на один. 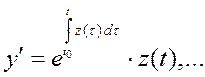 .
Подставим =>
.
Подставим => 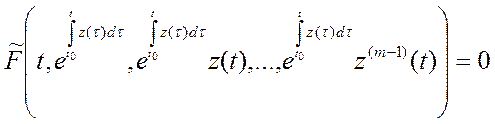 (при
(при ![]() )
)![]()
Понятие диф. уравнение. Примеры.
Рассмотрим функцию ![]() ,
,![]() ,
, ![]() ,
, ![]() Т.е.
функция (2n+1)-переменных. Найдем
Т.е.
функция (2n+1)-переменных. Найдем ![]() ,
, ![]() такая, что (*)
такая, что (*)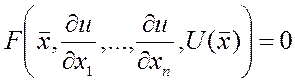 -дифференциальное
уравнение с частными производными 1 порядка. Проблема заключается в поиске
-дифференциальное
уравнение с частными производными 1 порядка. Проблема заключается в поиске ![]() . Если
. Если ![]() - при x-одномерное
=>это обыкновенное уравнение 1 порядка. Обычно записывают
- при x-одномерное
=>это обыкновенное уравнение 1 порядка. Обычно записывают ![]() . Т.е.
. Т.е. 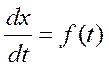 ,
, ![]() – задана, а
– задана, а ![]() – надо
найти. Если
– надо
найти. Если ![]() (начальное состояние), то определение
(начальное состояние), то определение ![]() => однозначное определение. Пример:
субстанция, вообще уравнение это связь между субстанцией и скоростью. Пример:
=> однозначное определение. Пример:
субстанция, вообще уравнение это связь между субстанцией и скоростью. Пример:
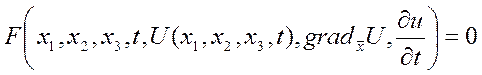 . Если система уравнений, то просто в (*)
ставим над x черточку =>
. Если система уравнений, то просто в (*)
ставим над x черточку => ![]() и над
и над ![]() => система дифференциальных уравнений
m-того порядка:
=> система дифференциальных уравнений
m-того порядка: 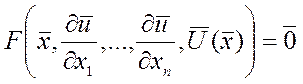 . И для обыкновенного:
. И для обыкновенного: ![]() m-того порядка.
m-того порядка.
Уравнения второго порядка
![]() ,
, ![]() ,
, ![]() . Вторые
производные - это симметрические матрица
. Вторые
производные - это симметрические матрица ![]()
![]() )
=> переменных =
)
=> переменных = 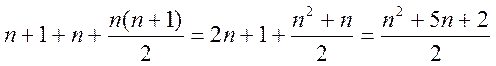
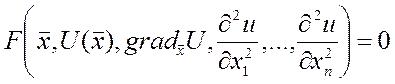 -
дифференциальное уравнение 2-ого порядка. Если размерность x-единица, то
-
дифференциальное уравнение 2-ого порядка. Если размерность x-единица, то ![]() -обыкновенное дифференциальное уравнение
2-го порядка. Если субстанция, то grad =>скорость;
-обыкновенное дифференциальное уравнение
2-го порядка. Если субстанция, то grad =>скорость; 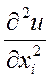 =>ускорение.
=>ускорение.
Примеры:
1.
Рассмотрим уравнение 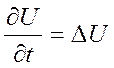 ,
, 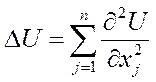
![]() ,
, ![]()
Это линейная функция – уравнение теплопроводности (диффузии).
2.
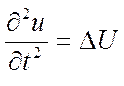 -
волновое уравнение (линейное) (описывает колебательный процесс) - это колебание
однородной струны.
-
волновое уравнение (линейное) (описывает колебательный процесс) - это колебание
однородной струны.
3.
![]() -
уравнение Лапласа(для стационарного процесса всё устоялось)
-
уравнение Лапласа(для стационарного процесса всё устоялось)
4.
![]() уравнение Гельмгольца.
уравнение Гельмгольца. ![]()
5.
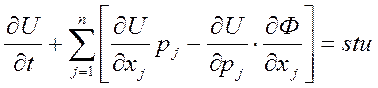 - уравнение кинетическое. Ф(x,t)
– потенциал, p – потенциал, t
– время,
- уравнение кинетическое. Ф(x,t)
– потенциал, p – потенциал, t
– время, ![]() -
положение, точка пространства. U
- распределение частиц(её интеграл дает количество частиц). Stu
столкновение частиц. Если stu
равно нулю, то непрерывность движения.
-
положение, точка пространства. U
- распределение частиц(её интеграл дает количество частиц). Stu
столкновение частиц. Если stu
равно нулю, то непрерывность движения.
6.
Уравнение переноса (движение заряженных частиц) , если справа не 0, а 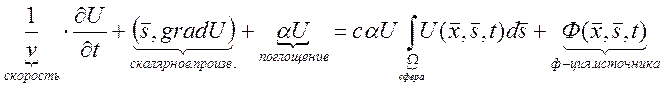 Если справа не 0, Ф(…)
=> неоднородное уравнение.
Если справа не 0, Ф(…)
=> неоднородное уравнение.
7.
(*)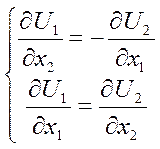 , 2 функции
, 2 функции ![]() и
и ![]() ,
это линейная система уравнений первого порядка. Это система Коши - Римана –
Даламбера - Эйлера. Если взять
,
это линейная система уравнений первого порядка. Это система Коши - Римана –
Даламбера - Эйлера. Если взять ![]() и
записать ряд
и
записать ряд 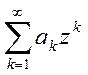 ,то ряд записывается =
,то ряд записывается = ![]() .
Если ряд сходится в области, то U1
и U2
будут удовлетворить той системе уравнений(*). Потоки (любые) хорошо описываются
такими функциями.
.
Если ряд сходится в области, то U1
и U2
будут удовлетворить той системе уравнений(*). Потоки (любые) хорошо описываются
такими функциями.
8. Максвелл: система, описывающая магнитные поля:
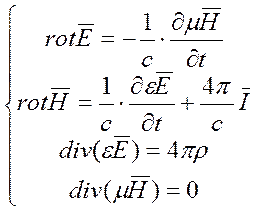
9.
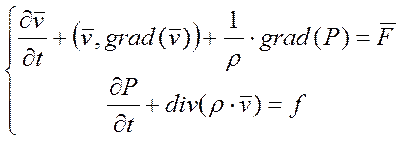
![]() - функции источника. Это
уравнение Эйлера - газовой динамики. Это нелинейная система.
- функции источника. Это
уравнение Эйлера - газовой динамики. Это нелинейная система.
10.
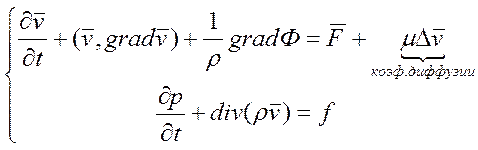 при наличии вязкости это уравнение
потрясающе описывает.
при наличии вязкости это уравнение
потрясающе описывает.
11.
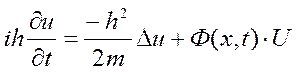 (это уравнение Шредингера) - линейное
уравнение в комплексной плоскости. u
-комплексозначная , h - постоянная
Планка,
(это уравнение Шредингера) - линейное
уравнение в комплексной плоскости. u
-комплексозначная , h - постоянная
Планка, ![]() , u-волновая функция(сама
не имеет физического смысла, но её модуль имеет).
, u-волновая функция(сама
не имеет физического смысла, но её модуль имеет).
Модуль
U ![]()
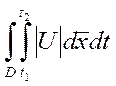 -
вероятность пребывания частицы в области D
-
вероятность пребывания частицы в области D
Задача Коши для обыкновенного диф. уравнения.
Будем рассматривать уравнения 1-го порядка типа
1)
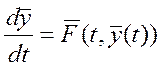 ; F
– непрерыв. ф-ии,
; F
– непрерыв. ф-ии, ![]() =
(y1,
…, ym), F
= (F1,
…, Fm),
=
(y1,
…, ym), F
= (F1,
…, Fm), ![]()
2)
![]()
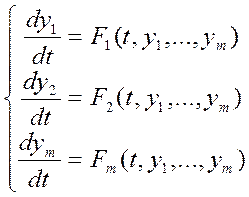
Если есть другие разрешённые уравнения, то они тоже сводятся к этой системе.
Это
задача Коши (если + задаётся![]() ) – поиск решений
системы уравнений!
) – поиск решений
системы уравнений!
Если
m=1![]()
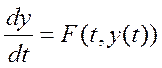 и
и
![]() - это задача Коши для одного уравнения
- это задача Коши для одного уравнения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.