Геом.смысл:
F(t,y(t)) – определяет tg угла наклона касательной
Т.е. опред. поле направлений
Если F – непрерывна в прямоугольнике, то
решение существует (по Т. Пеано)
Нужны
доп. условия ![]() Условие Липшица:
Условие Липшица: ![]() для
любого y1
и y2
из области ( k – константа)
для
любого y1
и y2
из области ( k – константа)
Задача Коши для обыкновенных диф.ур-ий:
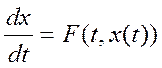 ,
, ![]()
Начальные условие: х(0) = х0. Задача – найти решение, подчин. начальному условию.
Система
получается, если над всеми х поставить вект. ![]()
Пример:
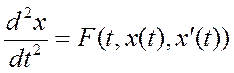 -
ур-е 2-го порядка
-
ур-е 2-го порядка
Полагаем
![]()
(*)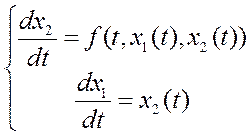 , уравнения 1-ого порядка
, уравнения 1-ого порядка
А в задаче Коши ![]() => система (*) + эти данные
=> система (*) + эти данные ![]() , а
, а ![]()
Аналогично для любого уравнения более высокого порядка
Т.Пеано: задача Коши имеет решение в случаеn=1
Но оказывается, что это решение не единственно
Если f – обладает регулярным свойством, т.е.
![]() - условие Липшица
- условие Липшица
![]() – для n переменных
условие Липшица. Тогда, если f – непрерывна в области
определения ,и по переменной существует условие Липшица => существует
единственное решение в окрестности точки t0=t(0)
– для n переменных
условие Липшица. Тогда, если f – непрерывна в области
определения ,и по переменной существует условие Липшица => существует
единственное решение в окрестности точки t0=t(0)
Свойства гармонических функций ( без доказательства только формулировку).
Определение: функция
U(x,y,z) называется гармонической в области D,
если ![]() частная производная до 2 порядка
частная производная до 2 порядка ![]() и удовлетворяет уравнению Лапласа
и удовлетворяет уравнению Лапласа 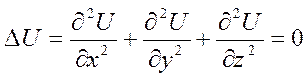
Если n=2 => 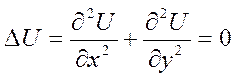 . Если n=1 =>
. Если n=1 => 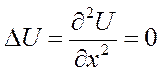
Примеры: если n=1 => U=kx+b – неинтересно
Тогда будем изучать ![]()
Пример: U=const; ax+by+cz+d для n=3
Если n=2,
а 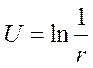 , а
, а ![]()
n=3
=> 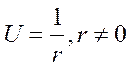 , а
, а ![]()
Свойства:
1. Формула Грина:
n=3 пусть есть ![]() , D – ограниченная
область.
, D – ограниченная
область. ![]() - непр. диф-ма с границей
- непр. диф-ма с границей
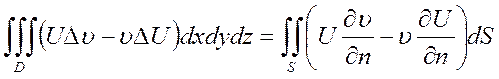
n - вектор внешней нормали
![]() -производная по направлению вектора
внешней нормали
-производная по направлению вектора
внешней нормали
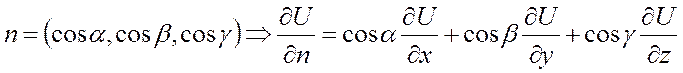
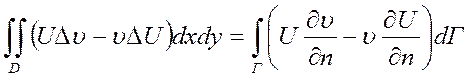
2. Необходимое условие гармоничности:
Если U – гармонич. в области D (огранич) и непр диф-ма
1 раз в
замыкании 
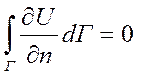 n=2
n=2
Доказательство:
по условию U-гарм. ![]()
Подст в
ф-лу Грина, а вместо ![]() (гарм)=1
и =>
(гарм)=1
и =>
0= ч.т.д.
ч.т.д.
3. Теорема: интегральное представление гармонической функции)
Если U гармонич в огр. области D и
непредельно диф-ма в ![]() =>
=> 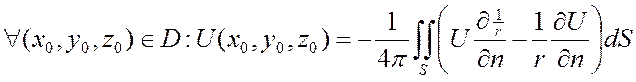 :
:
n=2: 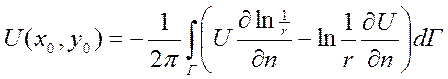 ,
, 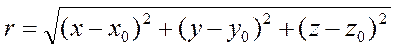
Доказательство: восп. ф-лой Грина. Построим шар вокруг ![]() радиуса
радиуса ![]()
![]() -шар
-шар
![]()
Если закрытый шар=>
![]()
![]() - в этой области функция гармонич
- в этой области функция гармонич 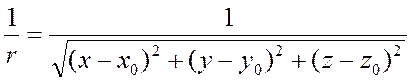 , а U – гармонич. во всей области => у нас есть 2 гармонич. ф-ции
=> по ф-ле Грина
, а U – гармонич. во всей области => у нас есть 2 гармонич. ф-ции
=> по ф-ле Грина
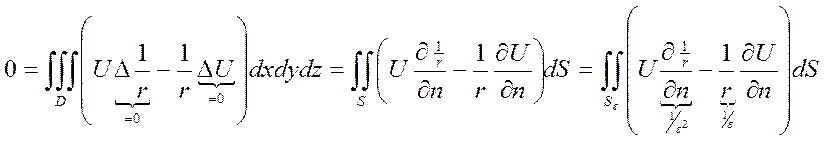 (*)
(*)
Рассмотрим второе слагаемое – пов. сферы.
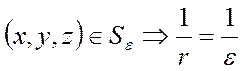 ,
, 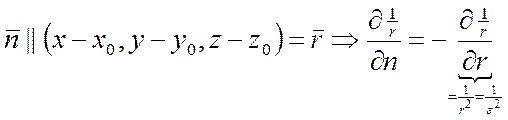
(т.к.
направлен в разные стороны). Перепишем: ![]()
 (по теореме о среднем)
(по теореме о среднем) 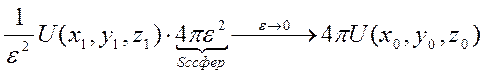 . Первый интеграл = 0 по необх. усл-ю гарм
. Первый интеграл = 0 по необх. усл-ю гарм 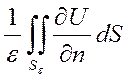 . В итоге (*)
. В итоге (*)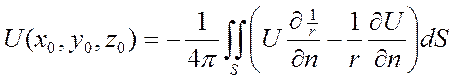 ч.т.д.
ч.т.д.
Следствие:
гарм ф-ция в D имеет частную производную ![]() порядка
порядка
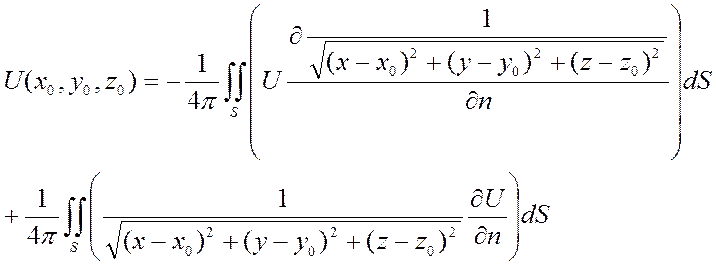 .
.
Первое
слагаемое ,
, ![]() -
диф-ма бесконечно, т.к. жнаменатель не 0.Со вторым аналогично
-
диф-ма бесконечно, т.к. жнаменатель не 0.Со вторым аналогично
4. Теорема о среднем: (для гармонич. Ф-ций)
U гармонич в обл D =>  ,
,
Если n=2 => 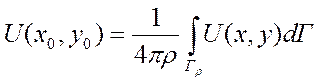
Доказательство: из интегральных представлений к границе шара:
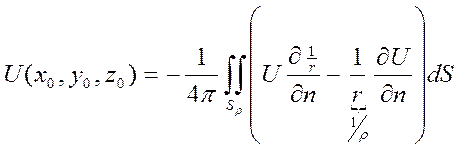 ,
, 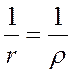 =>
второе слагаемое
=>
второе слагаемое 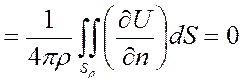 , по необх. призн. гарм. ф-ций
, по необх. призн. гарм. ф-ций
![]() ,
, ![]()
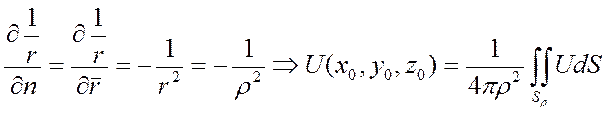 ч.т.д.
ч.т.д.
5. Принцип максимума:
Если U- гарм. в огр обл D, непр в D и если Uне const, то U не достигнет max и min в D, т.е. достигает max и min знач на границе
- не может быть
![]()
Док-во
: ![]() - непр в замкн
- непр в замкн
огр обл => по Th Вейерштрасса U-огр
достигает
![]() =>
=> ![]()
Теперь докажем, что внутри не достиг.
От
противного: допустим ![]() => докажем, что
=> докажем, что ![]() (во всей D).
Поэтому сначала покажем, что U=M
в шаре. Строим шар.
(во всей D).
Поэтому сначала покажем, что U=M
в шаре. Строим шар.
![]()
По Th о среднем допустим, что ![]() на сфере, и
на сфере, и ![]() окрестность
окрестность
![]() , где то <M по
теореме о среднем
, где то <M по
теореме о среднем
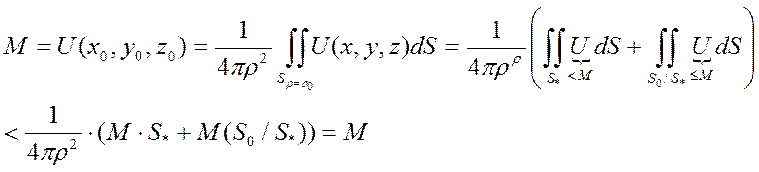
Поэтому у нас противоречие => на сфере функция U=M. Варьируем ![]() => U=M в
=> U=M в ![]() (в шаре) Теперь покажем для всей области
(в шаре) Теперь покажем для всей области
![]() (лучше вне шара)
(лучше вне шара)
Соед.
непр. кривой с ![]()
Непрер крив
– ![]()
Точка
пересечения шара и ![]() =>
=> ![]()
Тогда
аналогично показываем в шаре ![]() , что U=M. Затем
, что U=M. Затем ![]() и т.д. => придем к 0<
и т.д. => придем к 0<![]() точке
точке ![]() за конечное число шагов.
за конечное число шагов. ![]() =>
=> ![]() для
для ![]() точки из D => U=M
точки из D => U=M![]() D
противоречие условию ч.т.д.
D
противоречие условию ч.т.д.
Теорема о существовании
единственности решения задачи Коши для обыкновенного диф. уравнения ( для
случая одного уравнения: 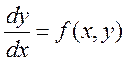 )
)
Теорема : Если
функция ![]() ,
,![]() ,
,![]() ,-
непрерывна и удовлетворяет условию Липшица:
,-
непрерывна и удовлетворяет условию Липшица:
![]() .
Тогда задача Коши (1) имеет единственное решение (1)
.
Тогда задача Коши (1) имеет единственное решение (1)  при
условии, что
при
условии, что ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.