Система линейных однородных уравнений с постоянными коэффициентами и её общее решение (все теоремы n-ного порядка), страница 5

Контрпример: рассмотрим 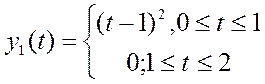. Это тонкий момент!

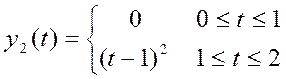. Они линейно независимы, так как С₁y₁(t)+C₂y₂(t)=0C₁ и C₂=0, а B(t)0 (так как строка или столбец)=0.

Утверждение 3:

Уравнение (1) имеет n линейно- независимых решений y₁(t), y₂(t),…, y_n(t); a.

Доказательство:

Рассмотрим произвольную матрицу размера n*n, так чтобы det . .

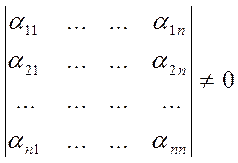Построим систему функций y_k(t):  строим y_k(t), так что первый столбец совпадает с данными Коши для y₁(t₀)  и так далее 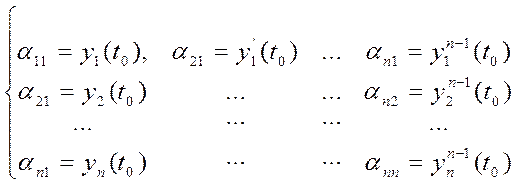. Заметим что B(t₀) – совпадает с det (). Так как задача Коши имеет единственное решение,

следовательно получаем систему функций y_k(t) – каждая из функций является решением. Они линейно независимы, так как B(t) при любом tсистема линейно независима. Ч.Т.Д.

Линейное неоднородное уравнение n-ного порядка. Общее и частное решение. Примеры частного решения.

Теорема.

 Любое решение y(t) неоднородного уравнения (2) представляется в виде y(t) = 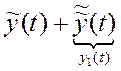, где - общее решение однородного уравнения, а  - частное решение неоднородного уравнения.

Доказательство:

, что если уравнения, то все коэффициенты могут быть найдены! Покажем это:

ФСР(1) – это y₁(t), y₂(t),…, y_n(t), то 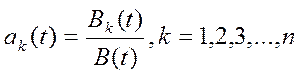. . 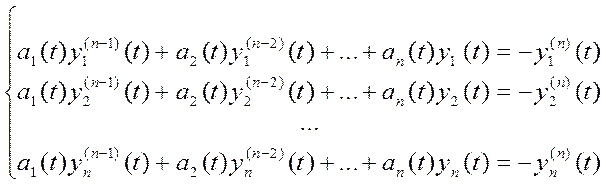Det (системы) = B(t)по Крамеру (каждый столбец заменяем) Получим B_k(t). ВСЁ!!!

Задача Коши для волнового уравнения.

1)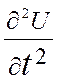= 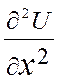- гиперболическое Ур-е    0 ≤ X ≤ π , t ≥ 0

(2) = U₀(x)                  (3) 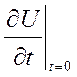=U₁(x)                        (4) U(0,t) = U(π,t)

U(x,t) = T(t)X(x)   → T’’(t)X(x) = T(t)X’’(x)  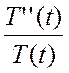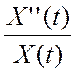→  =  =  -λ;  λ = n²   → 

→ T’’(t) + n² T(t) = 0  →  T(t) = a_ncos(nt) + b_nsin(nt) , где а_n и b_n – произв. const   →

→ U(x,t) =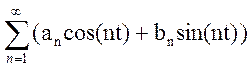

t=0 → ,

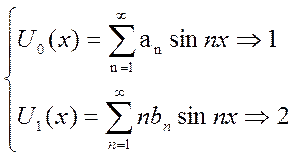где 1-находим а_n(коэф. Фурье.) нечетно продолж.  U₀(x)

2- b_n(коэф. Фурье.) нечетно продолж.  U₀(x)  вычисляем, ряды сх-ся

В первом случае: если U₀(x) имеет непр. произв. (в 0 → 0) продолжаем нечетн. обр.

Во втором случае: f – непр. диф-ма , в нуле – ноль  продолжаем нечетн. обр.

мы можем воспользоваться ф-лами для начальной краевой задачи

Формула Даламбера.

Th: Пусть U₀(x) и U₁(x) – дважды непрерывно дифференцируемые ф-ции, тогда задача Коши имеет решение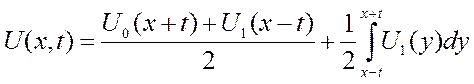 - формула Даламбера

Доказательство: покажем, что при t = 0    U₀(x) и U₁(x)  - есть решение:

Подставим t = 0  U(x,0) = U₀(x) – одно есть

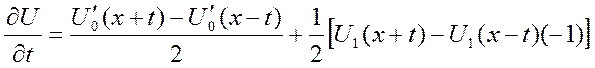
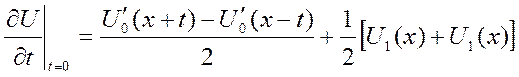   - второе есть

Покажем, что удовлетворяет ур-ию колебаний:

U(x,t) = f(x+t) + g(x-t) – где f,g – некоторые ф-ции  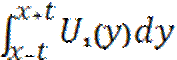=>   = [Ũ(x+t) – Ũ(x-t)] по Ньютону-Лейбницу

Подставляем  f =>  , а для g:

Т.е. каждая ф-ция – решение волнового ур-ия  => сумма линейных колебаний тоже решение.  f и g – 2 волны.

Докажем единственность:

(I способ) замена  ξ = x + t ;η = x – t  => x = (η + ξ)/2; t = (ξ - η)/2

Будем диф-ать

U(x,t) = U() = V(ξ ,η)

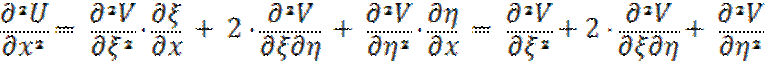
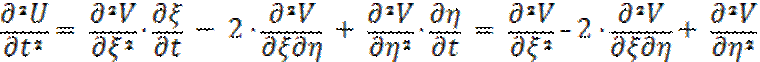
Приравняем    =      =>          =>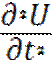   

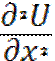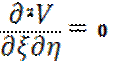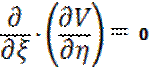
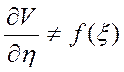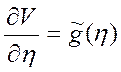=> , а V = g(η) + f(ξ)  подставляем в U(x,t) = f(.) + g(t)

Если  =>    U(x,t) = f(x + ct) + g(x - ct)  (по Д.)

(II способ) докажем, что  U(x,t) = g(x - t) + f(x + t)

U|_t=0 = f(x) + g(x)           U₁(x) = |_t=0 = f’(x) - g’(x)  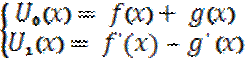  =>            (1)

Проинтегрируем U₁ от 0 до x  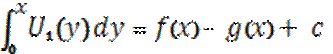=>          (2)

Сложим (1) и (2):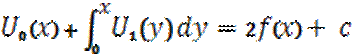   

Вычтем:    =>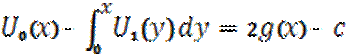 

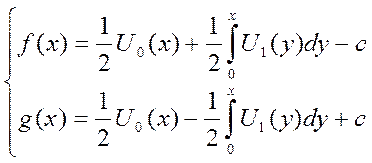
Подставим 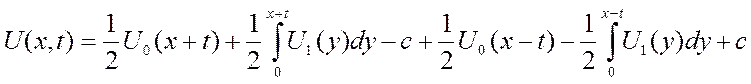 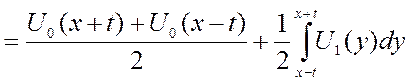- это и есть формула Даламбера

Т.е.  решение задачи Коши задается этой формулой

Операторные формулы в задаче Коши и управления.

рассмотрим такую задачу коши                                    

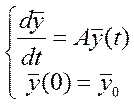
нам надо построить  решение для t> или <0

если

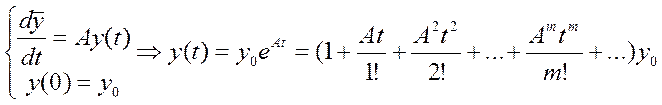
если туда подставить вместо числа А матр А получим:(t)=e^tA;

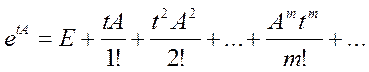
такой ряд сходится, он определяет матрицу.

тогда эта вектор-функция – решение задачи Коши. Проверка такая же.

Задача управления:

;     

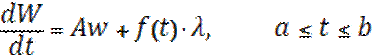,  - линейное пространство; W – это аналог у

A – оператор: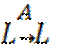

f(t) – непрерывная функция, > 0.

Уравнение – эволюционное, неоднородное

Задаются 2 условия:

(1)

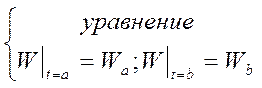
Задача: W(t) - ?

f(t) – известная числовая функция

“Перевод субстанции из W_a в W_b” – задача

Если А – число => обычное ур-е 1-го порядка

Формулы для решения:

Т1: Задача упр.(1) имеет решение

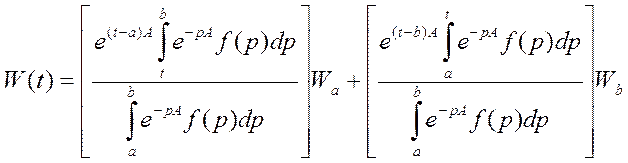
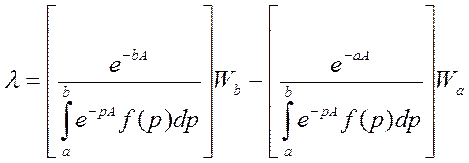
 - это операторная функция

матриц-функция (вместо А  z, раскл.в ряд Тейлора, а затем z A)

Покажем, почему это и есть решения: