Операторные формулы в задачи Коши и управления. Формальные операторы формулы, дающие решение задачи Коши (ряд сходится)
Нужно написать операторные формулы в задачи Коши и управления +
Общая ситуация
(1) ![]() =LU L – (втор. порядка) лин. опер. не зависит от t
=LU L – (втор. порядка) лин. опер. не зависит от t
L=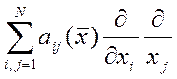 +
+ 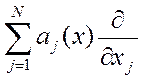 + о(x),
+ о(x),
где 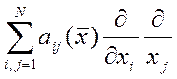 - диффузия,
- диффузия, 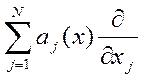 - перенос, о(х) – поглощение
- перенос, о(х) – поглощение
(2)![]() = U0(
= U0(![]() ),
),![]() ЄD (3) αU + β
ЄD (3) αU + β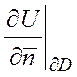 = 0 (α
и β - const) – ур-е
непротекания
= 0 (α
и β - const) – ур-е
непротекания
Смешанная краевая задача
Попробуем метод Фурье:
U(x,t) = T(t)X(x) – будем искать
Вставляем в (1) → T’(t)X(![]() ) = T(t)LX(
) = T(t)LX(![]() ) →
) → 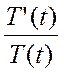 = L
= L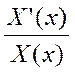 = -λ – const
= -λ – const
(5)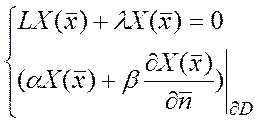 = 0 – это нач. краевая задача
= 0 – это нач. краевая задача ![]() ЄD ;
ЄD ;
![]()
Это основная задача спектрального анализа
λn n = 1,2,3… - собственные значения
Xn(![]() ) - собственная
функция
) - собственная
функция
T(t) = e-λnt → U(x,t) = 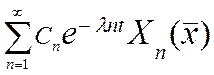
Cn
определяется из начального условия: 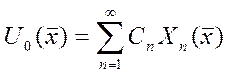 Если вместо (1) -
Если вместо (1) - 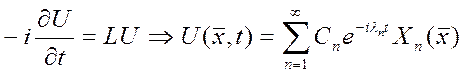
Понятие задачи вариационного исчисления.
Функционал (веществ.)
функция, определенная на множестве метрических пространств. Функционал I(y) – вещественная функция. y ![]() M – метрическое
просранство.
M – метрическое
просранство.
Опр: Элемент yо ![]() M
называется точкой максимума (минимума) функционала если
M
называется точкой максимума (минимума) функционала если ![]() окрестность точки yо,
такая что для всех y
окрестность точки yо,
такая что для всех y![]() этой окрестности I(y)
этой окрестности I(y)![]() I(yо) (min)
или I(y)
I(yо) (min)
или I(y)![]() I(yо)(max)
I(yо)(max)
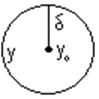 Y0
Y0 ![]() M
Это экстримум (локальный)
M
Это экстримум (локальный)
Пример: y(x): x![]() [a,b] , y(x) – непрерывна, диф. Функция класса C1
[a,b] , y(x) – непрерывна, диф. Функция класса C1
y(a)=A и y(b)=B
 I(y) =dx
– длина графика этой функции I(y)=min, когда y(x)
линейная
I(y) =dx
– длина графика этой функции I(y)=min, когда y(x)
линейная
Будем полагать, что M – линейное пространство.
Уравнение Эйлера.
Лемма: если y0![]() M (лин.метр.пр-во) дает экстремум функционалаI(y), тогда если существует,
M (лин.метр.пр-во) дает экстремум функционалаI(y), тогда если существует,
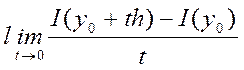 ,
, ![]() h
h ![]() M, и (y0 + th)
M, и (y0 + th)![]() M, а t
M, а t ![]() 0 то этот предел равен нулю.
0 то этот предел равен нулю.
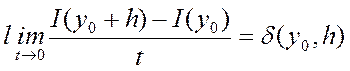 –
вариация функционала I(y) в
точке
–
вариация функционала I(y) в
точке ![]() (аналог теоремы Ферма)
(аналог теоремы Ферма)
Доказательство: рассмотрим
F(t)= I(y0 + ht) { y0,h – fix},
|t| ![]()
![]()
Это вещественная функция
т.к. при t=0, F(0)= I(y0) – max
или min => существует производная – это вариация,
а т.к. экстремум ![]() = 0 ч.т.д.
= 0 ч.т.д.
=> Необходимое условие экстремума: вариация равна нулю.
Будем рассматривать I(y) = 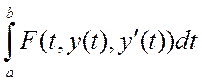 (1)
(1)
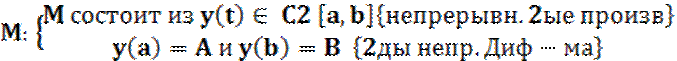
F (t, y, y’) – функция трех переменных (t, y, y’) класса C2 (R3)
Это вариационная задача с неподвижными концами
Tеорема:
Если y(t) дает экстремум
функционала (1) (max или min), y(t) ![]() M, тогда функция y(t)
является решением уравнения Эйлера.
M, тогда функция y(t)
является решением уравнения Эйлера.
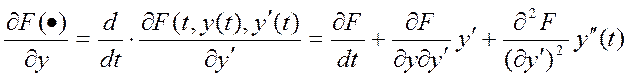
Док-во: т.к. существует
экстремум => ![]() (по лемме) -
(по лемме) - ![]() h(t) класса C2 так что h(a) = h(b) = 0
h(t) класса C2 так что h(a) = h(b) = 0
y(t) + ph(t) – рассмотрим такие функции
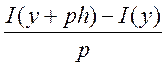
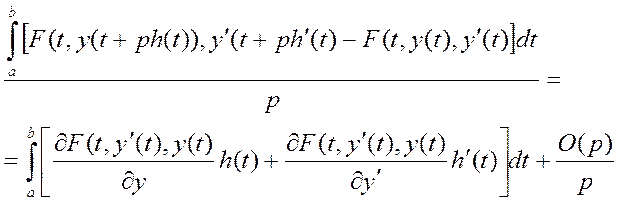
Если p→0 => I(y) =0, если y – экстремаль =>
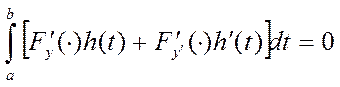 ,
, ![]() ,
, ![]() ,
перепишем
,
перепишем
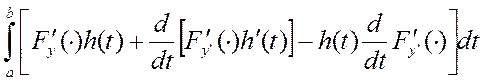 - это (*)
- это (*)
Т.к. 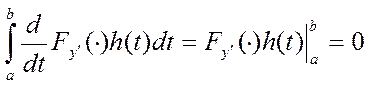 ,
т.к. h(a)=h(b)=0 =>
,
т.к. h(a)=h(b)=0 =>
![]() =
= 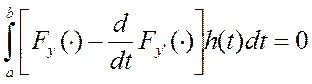 =>
=>
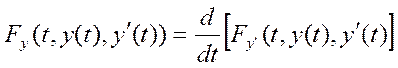 т.е. ур-ие Эйлера выполняется,
ч.т.д.
т.е. ур-ие Эйлера выполняется,
ч.т.д.
Распишем ур-ие Эйлера еще раз:
(2) ![]() ,
а если
,
а если ![]()
![]()
![]() ,
а
,
а 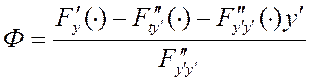 ур-ие второго порядка
ур-ие второго порядка
Любое решение ур-ия является подозрительным на экстремум (экстремаль, стационарн. реш.)
Пример1:
I(y) =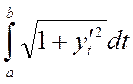 , y(a) = A , y(b) = B F =
, y(a) = A , y(b) = B F = 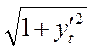 зависит только от y’
зависит только от y’
Из 2 =>
0 = 0 + 0 + F”y’y’(![]() )y” => 0 =
)y” => 0 =
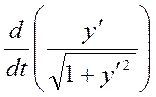 =>
=> 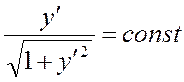
=> y’ = const
=> y(t) = kt + d
- линейная ф-ция, т.е. все экстремали 
Формула Пуассона
Интегральная формула Пуассона.
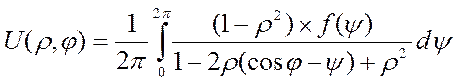 -
решение задано на D для круга.
-
решение задано на D для круга.
x=![]() cos
cos![]() ,
y=
,
y=![]() sin
sin![]() . Схема доказательства: переходим в
полярную систему координат:
. Схема доказательства: переходим в
полярную систему координат: 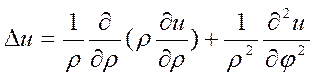 . Применяем метод
Фурье - метод разделения переменных. Ищем решение в виде
. Применяем метод
Фурье - метод разделения переменных. Ищем решение в виде ![]() Подставим в
Подставим в ![]() и
решаем
и
решаем![]() находим R и Ф.
находим R и Ф.
![]()
![]() - а линейная комбинация тоже решение
- а линейная комбинация тоже решение ![]()
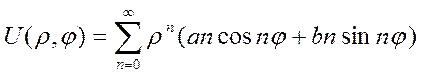
![]()
![]() находим через граничные условия =f.
находим через граничные условия =f. ![]()
Теорема об устойчивости – формулировка без доказательства
Теорема:
пусть 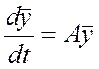 , А- постоянная квадратная матрица! Причем
корни
, А- постоянная квадратная матрица! Причем
корни ![]() характеристического уравнения
характеристического уравнения ![]() имеют неотрицательные вещественные части.
Тогда нулевое
имеют неотрицательные вещественные части.
Тогда нулевое ![]() решение
решение ![]() системы
системы
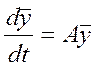 - устойчиво по Ляпунову (если все корни
строго отриц => асимптотич. устойч.)
- устойчиво по Ляпунову (если все корни
строго отриц => асимптотич. устойч.)
Теорема:
пусть ![]() ,
, ![]() -
вещественная диф. функция многих переменных
-
вещественная диф. функция многих переменных ![]() ,
обладающая свойством:
,
обладающая свойством:
1) функция ![]() - выпуклая и имеет в точке
- выпуклая и имеет в точке ![]() , т.е.
, т.е. ![]() -
минимум
-
минимум ![]()
2) 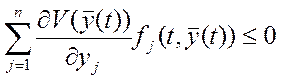 ,
,
![]() и
и ![]() решения
решения
![]() системы (1)
системы (1)
{система(1) 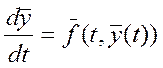 }
}
Тогда нулевое решение ![]() явл. устойч. по Ляпунову!
явл. устойч. по Ляпунову!
Система (1):
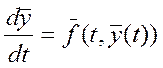 n- штук функций,
n- штук функций, ![]() - непрер. диф-ма
функция.
- непрер. диф-ма
функция.
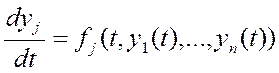
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.