 (1)
(1) 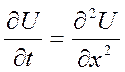 -
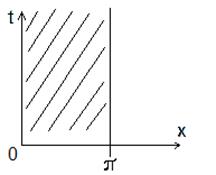
параболическое ур-е., 0 ≤ x ≤ π, на конеч. промежутке; t ≥ 0
-
параболическое ур-е., 0 ≤ x ≤ π, на конеч. промежутке; t ≥ 0
(2) ![]()
(3) U(0,t) = U(π,t)
Применяется метод разделения переменных – метод Фурье.
U(x,t) = T(t)X(x) – попробуем найти решение такого вида.
Подставим T’(t)X(x) = T(t)X’’(x) →
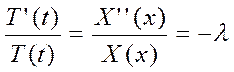 - const
- const
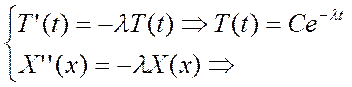
Кр.усл. → X(0)
= X(π) - задача на собств.
значения и собств. Функции, λ – собств. зн. и функции. Оказывается, что ![]() ; x’’ + n2x =
0
; x’’ + n2x =
0
![]()
![]()
![]() ,а
,а
![]() →
→ 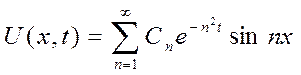
→решение пока без условия. ![]()
Теперь посчитаем Сn: U0(x) = ![]() =
=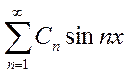 0 ≤ X ≤ π
0 ≤ X ≤ π
т.к. f
– нечетная, то U0(x)=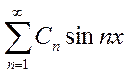 -π ≤ X ≤ π
-π ≤ X ≤ π
Cn
– коэф-ты Фурье, т.к. сход. равномерно, то Сn=![]()
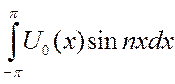
Рассмотрим другую задачу
(1)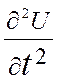 =
=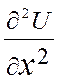 - гиперболическое
Ур-е 0 ≤ X ≤ π , t ≥ 0
- гиперболическое
Ур-е 0 ≤ X ≤ π , t ≥ 0
(2)![]() = U0(x) (3)
= U0(x) (3) 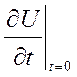 =U1(x) (4) U(0,t) = U(π,t)
=U1(x) (4) U(0,t) = U(π,t)
U(x,t) = T(t)X(x) → T’’(t)X(x) = T(t)X’’(x) → 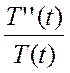 =
= 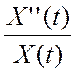 = -λ; λ = n2 →
= -λ; λ = n2 →
→ T’’(t) + n2 T(t) = 0 → T(t) = ancos(nt) + bnsin(nt) , где аn и bn – произв. const →
→ U(x,t) = 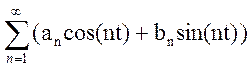
t=0
→ 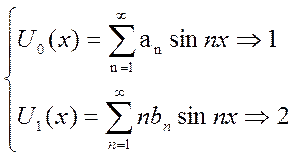 ,
,
где 1-находим аn(коэф. Фурье.) нечетно продолж. U0(x)
2- bn(коэф.
Фурье.) нечетно продолж. U0(x) ![]() вычисляем, ряды сх-ся
вычисляем, ряды сх-ся
В первом случае: если U0(x) имеет непр. произв.
(в 0 → 0) ![]() продолжаем нечетн. обр.
продолжаем нечетн. обр.
Во втором случае: f – непр. диф-ма , в нуле – ноль ![]() продолжаем
нечетн. обр.
продолжаем
нечетн. обр. ![]()
![]() мы можем
воспользоваться ф-лами для начальной краевой задачи
мы можем
воспользоваться ф-лами для начальной краевой задачи
Задача Коши для уравнения теплопроводности – доказательство формулы Пуассона ( в многомерном без доказательства)
(1) уравнение диффузии 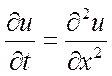 - параболическое уравнение
- параболическое уравнение ![]() ,
, ![]() ;
; ![]()
(2) начальные условия ![]() - задается это начальным состоянием.
- задается это начальным состоянием.
Это задача Коши.
Если функция огранич.![]() существует единственное решение.
существует единственное решение.
Теорема: пусть ![]() - огранич. дважды непрерывно диф-мая
функция и производные (первая и вторая) тоже ограничены. Тогда имеет место
формула для решения
- огранич. дважды непрерывно диф-мая
функция и производные (первая и вторая) тоже ограничены. Тогда имеет место
формула для решения ![]() задачи Коши (1), (2):
задачи Коши (1), (2): 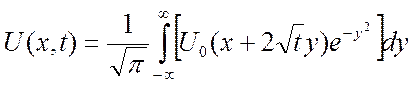 .
.
Покажем, что 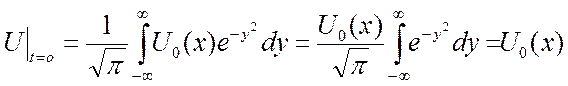 - да!
- да! ![]() формула
справедлива, удовлетворяет усл. (2)
формула
справедлива, удовлетворяет усл. (2)
Теперь докажем, что она удовлетворяет условию параболического уравнения:
Диф-ем по х: 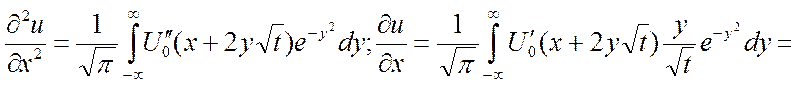
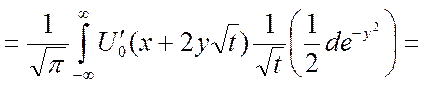 (по частному)
(по частному) 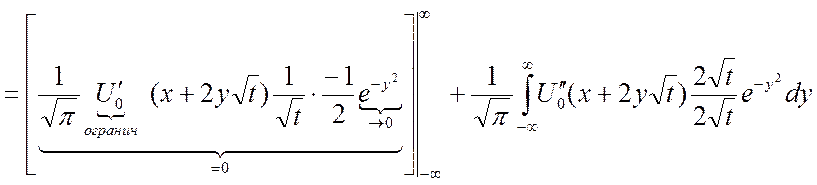 =
=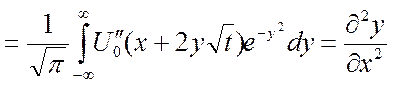 - верно! Всё
доказано))
- верно! Всё
доказано))
Приложение: Но можно было доказать иначе:
Замена 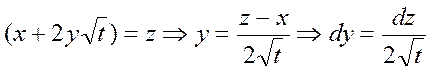
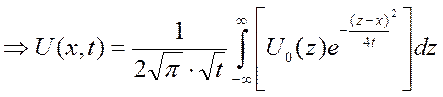 - Пуассона
- Пуассона
Вектор ![]()
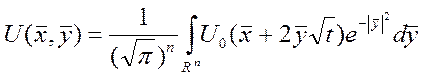
Это решение 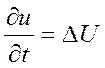 ;
; ![]()
![]()
![]() , если
, если 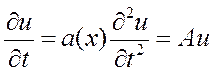 (эволюционные
уравнения), где
(эволюционные
уравнения), где 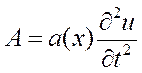 .
.
Можно рассматривать 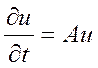 , где А – линейный оператор и не зависит от
t!
, где А – линейный оператор и не зависит от
t! ![]()
![]() -
формальное решение задачи Коши.
-
формальное решение задачи Коши. 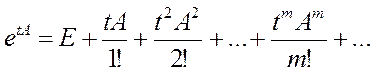
Метод «сплайн-функции»
На любом откр. промеж. ф-ция – полином, а в точках – так, чтобы ф-ция была непрерывна.
Определитель Вронского и его свойства
Определение: система функций
y1(t), y2(t),…, ym(t), ![]() называется
линейно зависимой на
называется
линейно зависимой на ![]() , если
, если ![]()
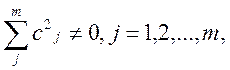 так что
так что 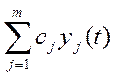 .
Линейно независимы
.
Линейно независимы![]() не удовлетворяет этому условию,
все
не удовлетворяет этому условию,
все ![]() =0.
=0.![]() критерий
зависимости и независимости: строится определитель Вронского:
критерий
зависимости и независимости: строится определитель Вронского: 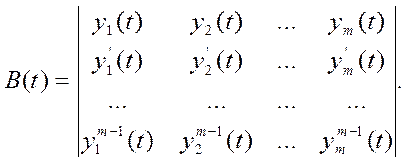
Теорема.
Если система функций линейно
зависима на отрезке ![]() , то на том же отрезке
определитель Вронского равен 0.
, то на том же отрезке
определитель Вронского равен 0.
Определитель Вронского:
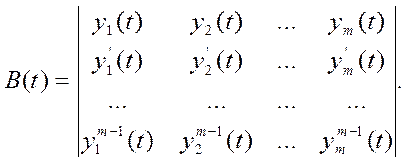
Доказательство:
Дано, что ![]() на отрезке
на отрезке ![]() , причем
не все ai равны нулю. Дифференцируя
тождество (n-1) раз, получим
, причем
не все ai равны нулю. Дифференцируя
тождество (n-1) раз, получим
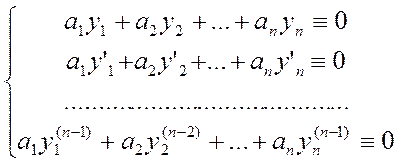 . Эта
линейная однородная по отношению ко всем ai
система n уравнений имеет нетривиальное решение (так
как не все ai равны
нулю) при любом значении t на отрезке
. Эта
линейная однородная по отношению ко всем ai
система n уравнений имеет нетривиальное решение (так
как не все ai равны
нулю) при любом значении t на отрезке ![]() . Следовательно, определитель системы,
являющийся определителем Вронского, равен нулю в каждой точке t
отрезка
. Следовательно, определитель системы,
являющийся определителем Вронского, равен нулю в каждой точке t
отрезка ![]() . Ч.Т.Д.
. Ч.Т.Д.
Теорема.
Если система функций имеет решение не равное нулю, а определитель Вронского не равен нулю, она линейно независима.
Утверждение 1:
Если система функций y1(t),…,ym(t) – линейно зависима, то B(t)=0, ![]() .
.
Доказательство:
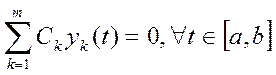 и
и 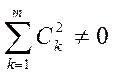 , так как линейно независимы.
, так как линейно независимы.![]() продифференцируем
продифференцируем![]()
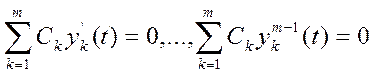
![]() получили m равенств. Если фиксируем t, то
получили m равенств. Если фиксируем t, то![]() система линейных алгебраических уравнений
относительно Ck. Хотя бы одно Ck
система линейных алгебраических уравнений
относительно Ck. Хотя бы одно Ck![]() система имеет
ненулевое решение C1, C2,
…, Cn.
система имеет
ненулевое решение C1, C2,
…, Cn.![]() det (однородной системы)= 0 = B(t),
det (однородной системы)= 0 = B(t), ![]() доказано
для
доказано
для ![]() (в
(в ![]() точке).
точке).
Утверждение 2:
Если система функций y1(t),…,ym(t) – линейно независима и каждая функция yk(t) – является решением уравнения (1) ![]() }.
Тогда B(t)
}.
Тогда B(t)![]() .
.
Доказательство:
Допустим, что ![]() так что B(t0) = 0. Тогда рассмотрим алгебраическую систему
уравнений
так что B(t0) = 0. Тогда рассмотрим алгебраическую систему
уравнений
B(t0)![]() ,
то есть
,
то есть 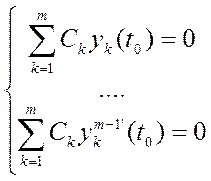 . Рассмотрим эту систему относительно Ck, так как B(t0) = 0
. Рассмотрим эту систему относительно Ck, так как B(t0) = 0![]()
![]() так что
так что 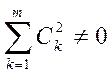 , -
решения этой системы. Рассмотрим y(t)=
, -
решения этой системы. Рассмотрим y(t)=
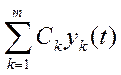 . (
. (![]() - решение
той системы). Будем брать производные и смотреть в
- решение
той системы). Будем брать производные и смотреть в ![]()
![]() . Эта функция является решением уравнения
(1), так как это линейная комбинация
. Эта функция является решением уравнения
(1), так как это линейная комбинация![]() по теореме о
единственности для задачи Коши
по теореме о
единственности для задачи Коши ![]() эта система функций
линейно зависима
эта система функций
линейно зависима![]() противоречию условию
противоречию условию![]() B(t)=0.
Ч.Т.Д.
B(t)=0.
Ч.Т.Д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.