Системы обыкновенных дифференциальных уравнений

Найти решения НЛДУ, удовлетворяющие поставленным начальным условиям:

239.  при

240.  при

241.  при

242.  при

243.  при

244.  при

245.  при

246. ,  при

10.7.    Системы обыкновенных дифференциальных уравнений

10.7.1. Основные понятия. Связь с дифференциальными

уравнениями  n – го порядка

1^°. Нормальные системы

Определение 1. Система обыкновенных ДУ вида

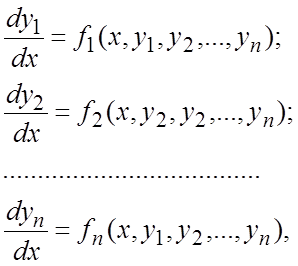                                                                               (7.1)

где  - неизвестные (искомые) функции,  -  известные функции, заданные и непрерывные в некоторой области, называется нормальной системой. Число n называется порядком системы (7.1).

Определение 2. Если правые части системы (7.1) являются линейными функциями от

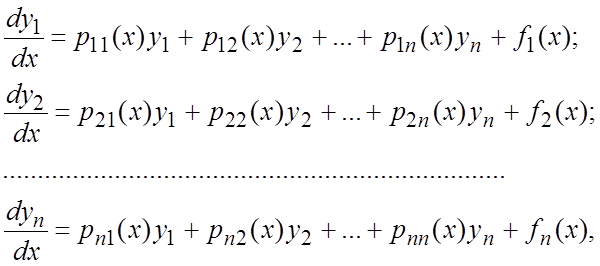                                              (7.2)

то такая система называется линейной.

Определение 3. Совокупность n функций

                                    ,                                   (7.3)  

определенных и непрерывно дифференцируемых в интервале (a,b), называется решением системы (7.1) в интервале (a,b), если функции (7.3) обращают (все) уравнения системы (7.1) в тождества (на интервале (a,b)). Кривая в (n+1) – мерном пространстве  соответствующая (7.3), называется интегральной кривой.

          Задача нахождения решения (7.3), удовлетворяющего начальным условиям

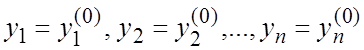                                   при ,                       (7.4)

где 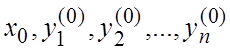 суть заданные числа (начальные данные), называется задачей Коши.

Теорема (достаточные условия существования и единственности решения задачи Коши). Пусть функции , в (7.1) определены в (n+1) – мерной области D изменения переменных . Если существует окрестность D точки 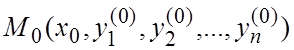, в которой функции   
а) непрерывны, б) имеют ограниченные частные производные по переменным , то найдется интервал  изменения x, в котором  существует и единственно решение нормальной системы (7.1), удовлетворяющее начальным условиям (7.4).

Определение 4. Совокупность n функций

                                         ,                                        (7.5)

определенных в некоторой области изменения переменных  и имеющих частные производные по x, называется общим решением (7.1) в области D изменения переменных , в каждой точке которой имеет место существование и единственность решения задачи Коши, если система (7.5)
1) является решением системы (7.1); 2) какие бы начальные условия (7.4) ни задать,  такие, что эти начальные условия будут удовлетворены.

Определение 5. Решение (7.3), в каждой точке которого имеет место существование и единственность решения задачи Коши, называется частным решением. Решение, в каждой точке которого нарушается единственность решения задачи Коши, называется особым.

Определение 6. Функция , определенная и непрерывная вместе с частными производными 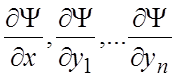 в некоторой области D изменения переменных и принимающая  постоянное значение при подстановке в нее произвольного решения системы, называется интегралом нормальной системы (7.1).Равенство

                                                           ,                                        (7.6)

где  - интеграл системы (7.1), а С – произвольная постоянная, называется первым интегралом системы (7.1).

Следующая теорема устанавливает условия того, что функция  является интегралом системы (7.1).

Теорема. Для того, чтобы функция  была интегралом системы (7.1.), необходимо и достаточно, чтобы было выполнено условие

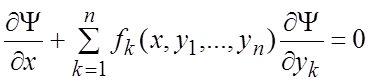                                           .                                  (7.6¢)

Определение 7. Совокупность n независимых первых интегралов системы (7.1) называется общим интегралом этой системы (первые интегралы называются независимыми, если входящие в них интегралы независимы).

2^°. Системы ДУ в симметрической форме.

Определение 8. Система вида

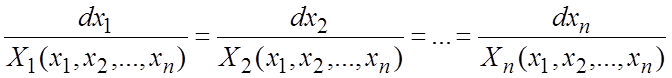             ,                      (7.7)

называется системой ДУ в симметрической форме. Если в точке 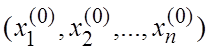 хоть один из знаменателей  отличен от нуля, то в окрестности этой точки систему (7.7) можно заменить нормальной системой из n-1 уравнений. Пусть 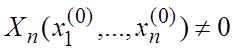. Тогда

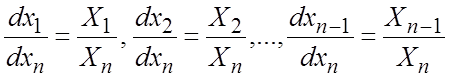                                .                                 (7.8)

Каждый интеграл (первый интеграл) системы (7.8) называется интегралом (первым интегралом) системы (7.7). Система (7.7) имеет не более чем n-1 независимых интегралов. Совокупность n-1 независимых первых интегралов системы (7.7) называют общим интегралом этой системы.

          Всякую нормальную систему (7.1) можно записать в виде (7.7):

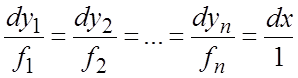                                              .                                         (7.9)

3^°. Канонические системы ДУ высших порядков.

Определение 9. Система ДУ высших порядков, разрешенная относительно старших производных, называется канонической. Она имеет вид

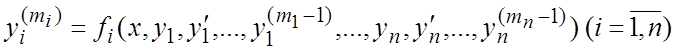                  .               (7.10)

Число  называется порядком системы (7.10). Каноническая система (7.10) (в частном случае – одно уравнение n-го порядка  приводится к соответствующей ей нормальной системе уравнений, если приять все производные, стоящие справа, за новые неизвестные функции.