Системы обыкновенных дифференциальных уравнений, страница 2

Замечание. Обратное, вообще говоря, неверно: не всякую систему ДУ можно свести к одному уравнению. Например, система  распадается на два независимых уравнения.

          Задача Коши для канонической системы (7.10) состоит в нахождении решения (7.3), в котором искомые функции  вместе со своими производными до порядков соответственно  принимают наперед заданные числовые значения при заданном значении x. Общее решение канонической системы (7.10) содержит  произвольных постоянных.

4^°. Примеры.

Пример 1. Привести каноническую систему дифференциальных уравнений

 к нормальному виду.

Решение. Положим . Тогда данную систему можно записать в виде: ,

которая и является нормальной системой четвертого порядка.

Пример 2. Привести к нормальной системе дифференциальное уравнение .

Решение. Положим ; тогда  и уравнение приводится к нормальной системе уравнений: .

Пример 3. Свести систему уравнений   (1) к одному уравнению и найти решение системы.

Решение. Найдем z из первого уравнения: . Отсюда имеем . Подставив значения z и во второе уравнение  системы, получим уравнение  - ОЛДУ с постоянными коэффициентами; его общее решение: . Из равенства  находим: и  система функций ,  (2) является решением исходной системы.

Пример 4. Показать, что решение (2) (см. пример 3) является общим решением.

Решение. 1.Подставляя функции  и  из (2) в систему (1), убеждаемся, что система функций (2)  является решением системы (1) (превращает каждое уравнение в тождество по x,  справедливое ).
2.Проверим выполнение условия 2) определения (7.5). В качестве области D системы (1) можно взять область D: ; при этом  выполнены условия теоремы Коши. Подставив  в систему (2), получим алгебраическую систему для определения постоянных

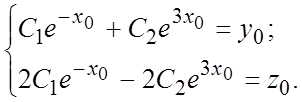                                                                                       (3)

Определитель этой системы   при  и, следовательно,  и  можно получить любое частное решение задачи Коши для системы (1).

Пример 5. Найти частное решение системы (1) (пример 3), удовлетворяющее начальным условиям:  при .

Решение. Подставляя начальные данные  в систему (3), получим: . Решая ее, найдем . Искомое частное решение .

Пример 6. Показать, что функция 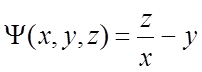 (3), определенная в области  является интегралом системы уравнений 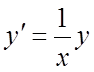,  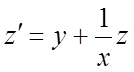(1), если общее решение этой системы есть ; (2).

Решение. Подставляя (2) в(3), получим =

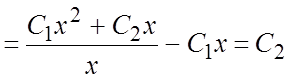  в области D. Следовательно, функция (3) является в области D интегралом системы уравнений (1), а значит первый интеграл (7.6) этой системы будет 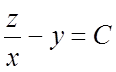, где С – произвольная постоянная.

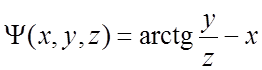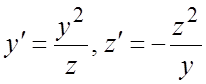Пример 7. Показать, что функция  (3) является интегралом  системы уравнений  (1).

Решение. В данном случае 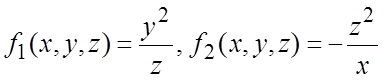 (2). Найдем частные производные данной функции (3):
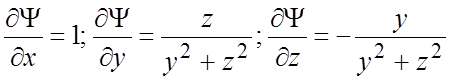                                    (4).

Подставляя (2) и (4) в левую часть (7.6¢), получаем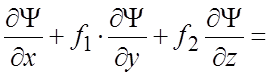

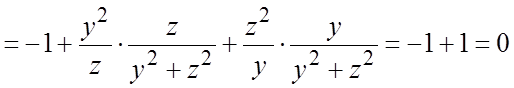 в области  и функция (3) есть интеграл системы (1) и, следовательно, первый интеграл (7.6) системы (1) будет 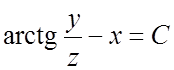, где С-  произвольная постоянная.

10.7.2.      Методы интегрирования нормальных систем

          В общем случае мы располагаем очень ограниченными возможностями интегрирования систем в квадратурах. Для линейных систем эти возможности несколько шире; но фактически всегда удается найти в квадратурах общее решение или общий интеграл лишь в случае, когда коэффициенты линейной системы являются постоянными.

1)      Сведение системы ДУ к одному или нескольким

         дифференциальным уравнениям

          Одним из методов решения систем ДУ является метод исключения неизвестных, который сводит систему уравнений к одному или нескольким уравнениям с одной неизвестной функцией в каждом (см. пример3, §10.7.1). Это приведение системы n-го порядка к одному уравнению n-го порядка (если оно возможно (см. замечания в п.3^°, §10.7.1)) достигается  последовательным дифференцированием одного из уравнений системы и исключением всех неизвестных функций, кроме одной (метод исключения). Проинтегрировав полученное уравнение, находят общее решение данной системы уже без новых квадратур. Заметим также, что во многих случаях этим методом удается проинтегрировать каноническую систему (7.10).

Пример 1. Для системы 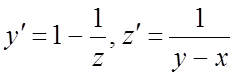 (1) найти  общее решение и выделить решение, удовлетворяющее начальным условиям: .

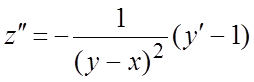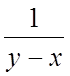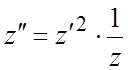Решение. Найдем общее решение системы (1) методом исключения. По этому методу дифференцирование начинают с того уравнения, которое содержит производную сохраняемой функции. Пусть мы хотим получить уравнение для  функции z. Дифференцируем второе уравнение (1): . Для исключения  и  из полученного уравнения, заменим в нем  и  их значениями из данной системы. Получим - уравнение второго порядка, допускающее понижение порядка. 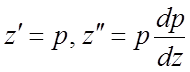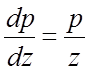Подстановкой  уравнение сводится к  и , откуда  и  и, таким образом, . Функцию y определим из второго уравнения (1): 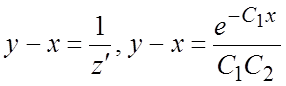, откуда 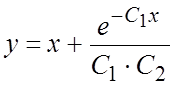. Общее решение системы (1) имеет вид: 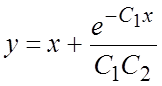, . Решим поставленную задачу Коши. Подставляя в общее решение вместо  и  их начальные значения 0, -1 и 1, получим систему для определения постоянных: 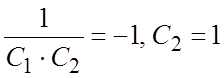, откуда , так что искомым решением будет . Других решений, удовлетворяющих заданным начальным условиям, нет.