Глава 9
Функции нескольких переменных
9.1. Основные понятия, определения
1°.![]() -
множество всех упорядоченных пар чисел (x,y) (троек чисел (x,y,z)).
-
множество всех упорядоченных пар чисел (x,y) (троек чисел (x,y,z)). ![]() - множество всех упорядоченных
наборов n чисел
- множество всех упорядоченных
наборов n чисел ![]() .
.
2°. Функция f n переменных
сопоставляет по определенному правилу каждому набору n
чисел ![]() из области определения
из области определения ![]() единственное значение u
из области значений
единственное значение u
из области значений ![]() , что записывается в
виде
, что записывается в
виде ![]() или
или ![]() В
дальнейшем будем рассматривать функции двух (трех) переменных
В
дальнейшем будем рассматривать функции двух (трех) переменных ![]() ,
, ![]()
![]() .
.
3°. Если (x,y) (или (x,y,z)) - декартовы координаты точки плоскости Oxy (или пространства Oxyz), то D – часть плоскости или вся плоскость (часть пространства или все пространство).
4°.e - окрестность точки ![]() -
множество всех точек
-
множество всех точек ![]() , не совпадающих с точкой
, не совпадающих с точкой ![]() , расстояние до которых от точки
, расстояние до которых от точки ![]() меньше e:
меньше e:
![]() . Так, e
- окрестность точки
. Так, e
- окрестность точки ![]() - множество точек M(x,y),
удовлетворяющих условию
- множество точек M(x,y),
удовлетворяющих условию 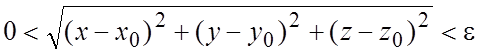 - шар радиуса e без границы с выколотым центром
- шар радиуса e без границы с выколотым центром ![]() .
.
5°. Назовем точку внутренней точкой области, если она принадлежит этой области вместе со всеми точками какой – нибудь своей окрестности. Любая окрестность граничной точки области содержит точки, принадлежащие области, и точки, не принадлежащие области. Сами граничные точки могут принадлежать области, а могут не принадлежать.
6°. Область называется замкнутой, если она содержит все свои граничные точки.
Пример 1. Найти и изобразить область определения функций:
а) 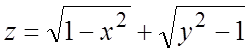 ; б)
; б) 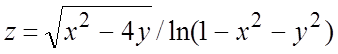 .
.
Ñ а) функция определена, если x и y удовлетворяют
системе неравенств (которую последовательно решаем)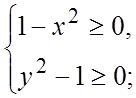
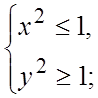
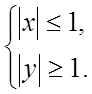 Следовательно,
область определения множество точек
Следовательно,
область определения множество точек ![]()
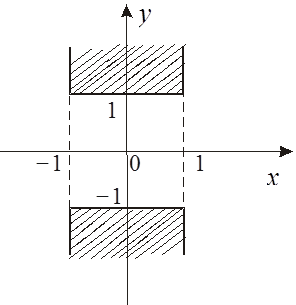
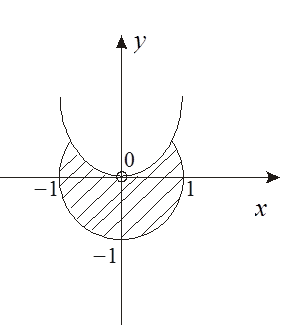
![]() .Область определения изображена на рис.
9.1.
.Область определения изображена на рис.
9.1.
 б) функция
определена, если x и y удовлетворяют системе неравенств
б) функция
определена, если x и y удовлетворяют системе неравенств
|
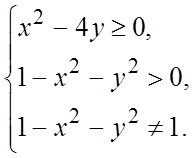
|
Задачи для самостоятельного решения
Найти области определения следующих функций:
1. 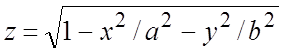 . 2.
. 2. ![]() . 3.
. 3. ![]() .
.
4. ![]() . 5.
. 5. 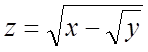 . 6.
. 6. ![]() . 7.
. 7. ![]() . 8.
. 8. 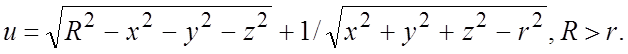
9.2. Предел функции
Пусть
функция ![]() определена на
множестве D и точка
определена на
множестве D и точка ![]() .
.
1°. Число А называется пределом
функции f(M)
при стремлении точки ![]() к точке
к точке ![]() (или,
другими словами, при
(или,
другими словами, при ![]() , если для любого, сколь угодно
малого положительного e найдется такая d- окрестность точки
, если для любого, сколь угодно
малого положительного e найдется такая d- окрестность точки ![]() ,
что для любой точки M из этой окрестности
выполняется
,
что для любой точки M из этой окрестности
выполняется ![]() и обозначается
и обозначается 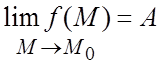
![]() . Этот предел не должен зависеть от
способа (“пути”) стремления M к М0.
. Этот предел не должен зависеть от
способа (“пути”) стремления M к М0.
Используя логические символы 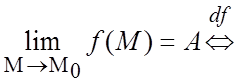
![]()
![]()
![]() .Для функции двух
переменных f (x,y)
.Для функции двух
переменных f (x,y) 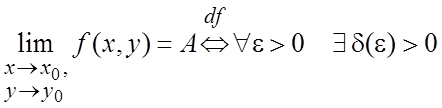
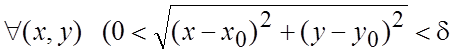
![]()
![]() .
.
2°. Функция f(M) называется бесконечно малой функцией (б.м.ф.)
при стремлении M к точке M0,
если 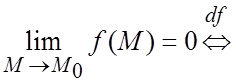
![]()
![]()
![]()
![]() . Практически, при
вычислении
. Практически, при
вычислении 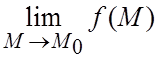 удобно задать проходящую через точки M и М0 линию в параметрической (или
иной ) форме, сведя тем самым задачу к вычислению предела функции одной переменной
по известным правилам и теоремам.
удобно задать проходящую через точки M и М0 линию в параметрической (или
иной ) форме, сведя тем самым задачу к вычислению предела функции одной переменной
по известным правилам и теоремам.
Пример 2. Вычислить пределы: а) 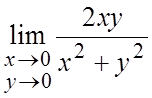 , б)
, б) 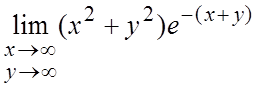
Ñ а) Пусть точка M(x,y) из окрестности точки M0(0,0) стремится к точке М0
по прямой y=kx (
проходящей через точки М0 и М). Тогда из ![]() следует
следует ![]() и
и 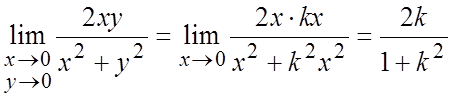 . Пределы получаются разными при различных
“k” и не существует числа A,
к которому значения
. Пределы получаются разными при различных
“k” и не существует числа A,
к которому значения 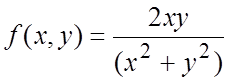 становились бы сколь угодно
близки, как только точка M(x,y) оказывается в достаточной близости от точки M0(0,0). Предел данной функции при M®M0(0,0) не существует.
становились бы сколь угодно
близки, как только точка M(x,y) оказывается в достаточной близости от точки M0(0,0). Предел данной функции при M®M0(0,0) не существует.
б) 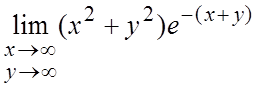 =½находим
предел вдоль луча y=kx
(k>0,
=½находим
предел вдоль луча y=kx
(k>0, ![]() ) при x®¥½=
) при x®¥½=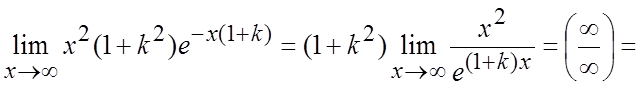 ½применим
правило Лопиталя два раза½=
½применим
правило Лопиталя два раза½=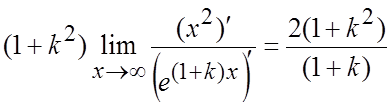 .
. 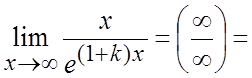
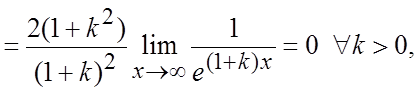 – предел существует и равен нулю. #
– предел существует и равен нулю. #
Вычислить пределы функций, полагая, что независимые переменные произвольно стремятся к своим предельным значениям.
9. 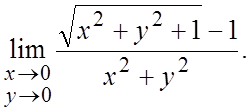 10.
10. 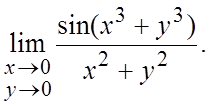 11.
11.
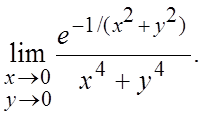
12. 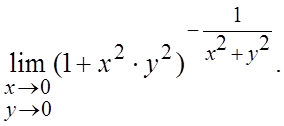 13.
13. 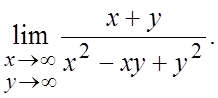
9.3. Непрерывность функции
1°. Функция f(M) называется непрерывной в точке ![]() ,
если выполнены условия : 1) f(M) определена в точке M0
; 2) существует
,
если выполнены условия : 1) f(M) определена в точке M0
; 2) существует 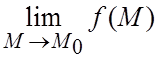 ;
;
3) 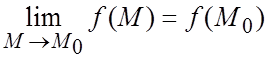 .
.
2°. Функция f(M) называется непрерывной в области U , если она непрерывна в каждой точке области U.
3° . Если в точке M0 нарушено хотя бы одно из условий 1) – 3) непрерывности функции в точке, то M0 называется точкой разрыва функции f(M). Точки разрыва могут быть изолированными, образовывать линии разрыва, поверхности разрыва и т.д.
Теорема
9.1 (Вейерштрасса). Если множество U, принадлежащее
области определения функции f, является
замкнутым и ограниченным, а функция f непрерывна
на U, то f
достигает на U своих наибольшего и наименьшего
значений, т.е. существуют такие точки ![]() и
и ![]() , что для любой точки
, что для любой точки ![]() выполняется неравенство
выполняется неравенство ![]()
Пример 3. Найти точки разрыва функций: а) ![]()
б) ![]()
Ñ а) Область существования функции ![]() есть множество точек плоскости Oxy, координаты которых удовлетворяют условию
есть множество точек плоскости Oxy, координаты которых удовлетворяют условию ![]() или
или ![]() -
внутренность круга радиуса
-
внутренность круга радиуса ![]() с центром в точке O (0;0). Функция
с центром в точке O (0;0). Функция ![]() не определена в
точках, в которых знаменатель обращается в нуль, т.е.
не определена в
точках, в которых знаменатель обращается в нуль, т.е. ![]() ,
отсюда
,
отсюда ![]() или
или ![]() . Таким
образом, функция z(x,y) разрывна на окружности
. Таким
образом, функция z(x,y) разрывна на окружности ![]() .
.
б) Функция u(x,y,z) не определена в
точках, в которых знаменатель обращается в нуль. Поэтому в пространстве Oxyz точки разрыва функции образуют поверхность ![]() – конус. #
– конус. #
Найти точки разрыва функций двух переменных:
14. ![]() 15.
15. ![]() 16.
16.
![]()
Найти точки разрыва функций трех переменных:
17. ![]() 18.
18. 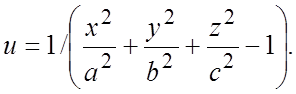
19*. Исследовать непрерывность функции при x = 0, y = 0:
1) ![]() . 2)
. 2) ![]() .
.
3) 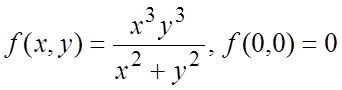 .
.
9.4. Частные производные и дифференцируемость функции
1°. Пусть M(x1,…,xk,…,xn) – произвольная фиксированная точка из
области определения D функции ![]() и точка
и точка ![]() Если
существует предел
Если
существует предел
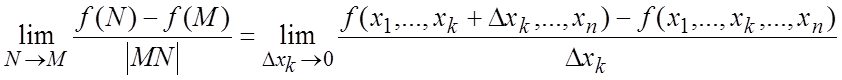 ,
,
то он называется
частной производной первого порядка данной функции по переменной xk в точке M и
обозначается 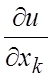 или
или ![]() , или
, или ![]() .
.
Частные производные вычисляются по правилам дифференцирования функции одной переменной, при этом все переменные, кроме xk , рассматриваются как постоянные.
2°. Частными
производными второго порядка функции ![]() по
соответствующим переменным называются частные производные от ее частных
производных первого порядка, они обозначаются:
по
соответствующим переменным называются частные производные от ее частных
производных первого порядка, они обозначаются: 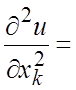
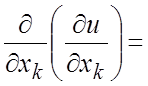 =
=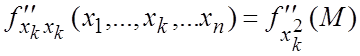 ,
, 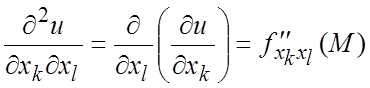 и т.д. Аналогично определяются частные
производные порядка выше второго.
и т.д. Аналогично определяются частные
производные порядка выше второго.
Теорема 9.2 Если смешанные производные ![]() непрерывны,
то они совпадают:
непрерывны,
то они совпадают: ![]() .
.
Таким образом, результат многократного дифференцирования функции по различным переменным не зависит от порядка дифференцирования при условии, что возникающие при этом “смешанные” частные производные непрерывны.
Пример 4. Найти частные производные первого и второго порядков от
функции ![]() .
.
Ñ Считая последовательно постоянной “y”, затем “x”, и применяя
правило дифференцирования сложной функции, получим: 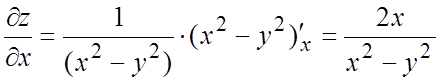 ,
,
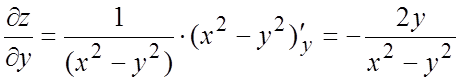 . Дифференцируя вторично, получим:
. Дифференцируя вторично, получим:
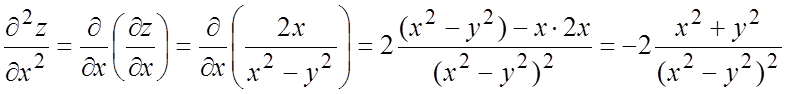 ,
,
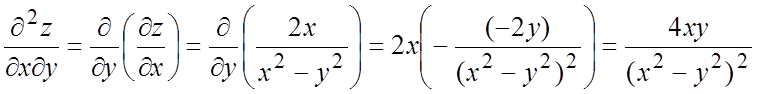 ,
,
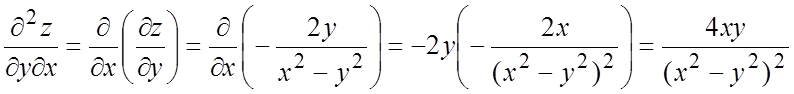 ,
,
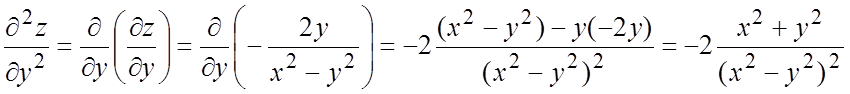 .#
.#
Найти частные производные 1-го и 2-го порядков от заданных функций:
20. ![]() . 21.
. 21. ![]() . 22.
. 22. ![]() . 23.
. 23. ![]() .
.
24. ![]() . 25. Найти
. 25. Найти ![]() , если
, если ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.