Определение 2. Функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() , если она определена в этой
точке и
, если она определена в этой
точке и 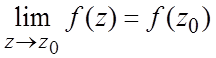 .
.
Определение 3. Функция ![]() ,
непрерывная в каждой точке области D, называется непрерывной в этой области.
,
непрерывная в каждой точке области D, называется непрерывной в этой области.
17. Изобразить множества; выяснить, какие из них являются областями, какие нет, какие из них - ограниченные области, какие не ограничены:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
; ![]() ;
;
д) ![]() .
.
18. Написать в комплексной форме уравнение следующих линий (t- действительный параметр):
а) ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) 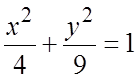 .
.
19. Какие линии заданы комплексным уравнением (t-действительный параметр):
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 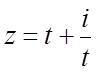 ; д)
; д)![]() ?
?
20. Для указанных функций найти действительную и мнимую части:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г)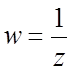 ; д)
; д)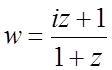 ; е)
; е)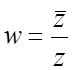 .
.
21. Найти образы данных точек при указанных отображениях:
а) ![]() ,
, ![]() ; б)
; б) ![]() ,
, ![]() ;
в)
;
в)![]() ,
, 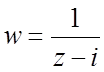 ;
г)
;
г) ![]() ,
, 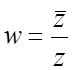 .
.
22. На какие линии плоскости (w) отображает функция ![]() следующие
линии плоскости (z): а) прямую
следующие
линии плоскости (z): а) прямую ![]() ; б) прямую
; б) прямую ![]() ;
в)гиперболу
;
в)гиперболу ![]() ; г)окружность
; г)окружность ![]() ?
?
23. Найти уравнение линий плоскости (w), на которые функция 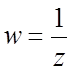 отображает следующие линии плоскости
(z): а)
отображает следующие линии плоскости
(z): а) 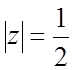 ; б)
; б) ![]() ; в)
; в)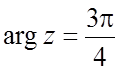 ;
;
г) 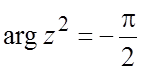 ; д)
; д) ![]() ; е)
; е) ![]() .
.
24. Выделить действительную и мнимую части у следующих функций:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() ;
;
ж) ![]() .
.
25.
Записать комплексные числа в показательной форме: а) 1; б) i; в) 1+i; г)![]() ; д)
; д)![]() .
.
26.
Вычислить: а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г) ![]() .
.
27.
Записать в алгебраической форме : а)![]() ; б)
; б)![]() ; в);
; в); 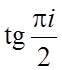 ; г)
; г)![]() ; д)
; д)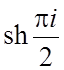 ; е)
; е)![]() .
.
28.
Вычислить: а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() .
.
29.
Найти: а)![]() ; б)
; б)![]() ; в)
; в)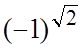 ; г)
; г)![]() ; д)
; д)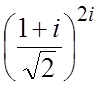 ; е)
; е)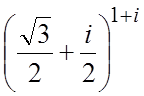 ; ж)
; ж)![]() .
.
Решить уравнения:
30. ![]() . 31.
. 31.![]() .
32.
.
32.![]() . 33.
. 33.![]() . 34.
. 34.![]()
![]() . 34.
. 34.![]() . 36.
. 36.![]() . 37.
а)
. 37.
а)![]() ; б)
; б)![]() .
.
Вычислить пределы:
38.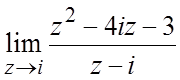 . 39.
. 39.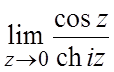 .
40.
.
40.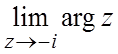 . 41.
. 41.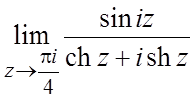 .
42.
.
42.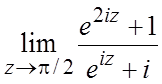 .
.
Доказать непрерывность на всей комплексной плоскости следующих функций:
43. ![]() . 44.
. 44.![]() .
45.
.
45.![]() . 46.
. 46.![]() .
.
Как доопределить данные функции в точке ![]() , чтобы они стали непрерывными в этой
точке:
, чтобы они стали непрерывными в этой
точке:
47.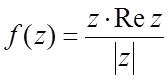 . 48.
. 48.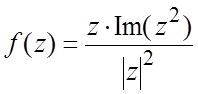 .
49.
.
49.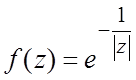 . 50.
. 50.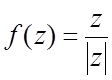 .
.
51.
Доказать, что функция ![]() не имеет предела при
не имеет предела при ![]() .
.
Указание. Положить ![]() , так что
, так что ![]() .
.
16.3. Аналитические функции. Условия Коши-Римана
16.3.1. Дифференцирование ФКП. Аналитичность функции
Определение 1. Функция ![]() называется
дифференцируемой в точке
называется
дифференцируемой в точке ![]() , если существует предел
, если существует предел
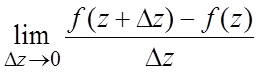
![]() .
(3.1)
.
(3.1)
Этот предел называется производной функции ![]() в точке z. Для нее употребляются обозначения
в точке z. Для нее употребляются обозначения 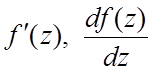 .
.
Теорема. Для того,
чтобы функция ![]() была дифференцируемой в точке z, необходимо и достаточно, чтобы
функции
была дифференцируемой в точке z, необходимо и достаточно, чтобы
функции ![]() ,
, ![]() были
дифференцируемы в этой точке и выполнялись условия Коши-Римана (говорят также
Даламбера-Эйлера):
были
дифференцируемы в этой точке и выполнялись условия Коши-Римана (говорят также
Даламбера-Эйлера):
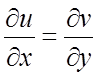 ;
; 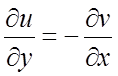 .
(3.2)
.
(3.2)
Определение 2. Функция ![]() называется
аналитической (регулярной) в данной точке
называется
аналитической (регулярной) в данной точке ![]() , если
она дифференцируема как в самой точке z, так и в некоторой ее окрестности.
, если
она дифференцируема как в самой точке z, так и в некоторой ее окрестности.
Определение 3. Функция ![]() называется
аналитической в области D,
если она аналитична в каждой точке этой области.
называется
аналитической в области D,
если она аналитична в каждой точке этой области.
Для любой аналитической
функции ![]() имеем
имеем
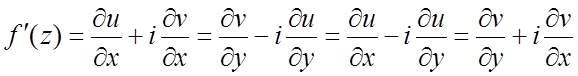 . (3.3)
. (3.3)
Заметим, что формулы дифференцирования ФКП аналогичны соответствующим формулам дифференцирования функций действительной переменной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.