Пример 7. Записать в полярной системе координат
область S - часть круга, ограниченную линиями ![]() ,
, ![]() ,
, ![]() (
(![]() ),
), ![]() - постоянные,
- постоянные, ![]() .
.
Ñ Изобразим область S (рис. 14.9). Запишем заданные линии
в полярных координатах, которые связаны с декартовыми формулами ![]() ,
, ![]() : 1)
: 1)![]() Þ
Þ ![]() ;
;
2) ![]() Þ
Þ![]() ,
, ![]() ;
;
3)![]() Þ
Þ![]() .
.
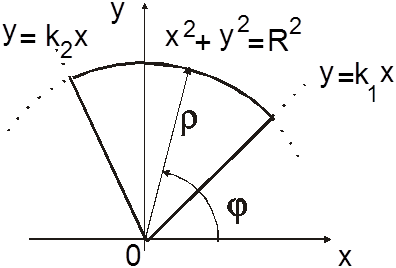 Область
Область ![]() переходит
в область
переходит
в область
![]() .
.
|
|
 Пример 8. Вычислить двойной интеграл
Пример 8. Вычислить двойной интеграл 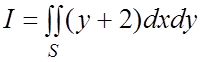 , S - множество точек, удовлетворяющих неравенству
, S - множество точек, удовлетворяющих неравенству ![]() .
.
|
Наличие в уравнении границы
комбинации ![]() наводит на мысль, что для вычисления
двойного интеграла удобно перейти к полярным координатам
наводит на мысль, что для вычисления
двойного интеграла удобно перейти к полярным координатам ![]() по формулам
по формулам ![]() ,
, ![]() ,
, ![]() . Уравнение границы
. Уравнение границы ![]() переходит в уравнение
переходит в уравнение ![]() или
или ![]() . Отсюда r=0 (соответствует полюсу O) и
. Отсюда r=0 (соответствует полюсу O) и ![]() - уравнение окружности. Так как
всегда
- уравнение окружности. Так как
всегда ![]() (по смыслу r), то из
(по смыслу r), то из ![]() следует
следует ![]() , отсюда получаем
, отсюда получаем 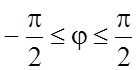 (этот же результат можно усмотреть
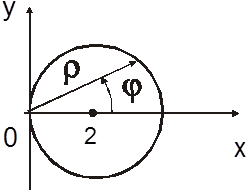
из рисунка). Итак, в полярных координатах область интегрирования есть
(этот же результат можно усмотреть
из рисунка). Итак, в полярных координатах область интегрирования есть 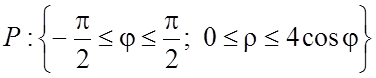 . Тогда по формуле (2.7)
. Тогда по формуле (2.7)
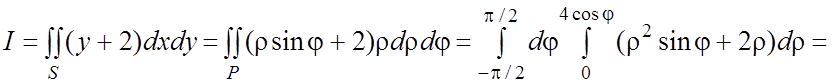
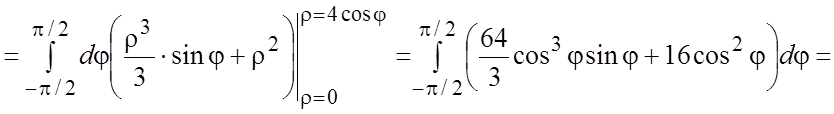
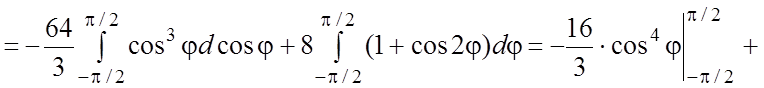
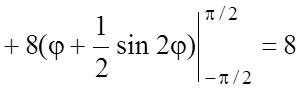 . #
. #
Пример 9. Вычислить 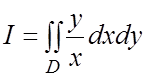 , где
, где ![]()
![]()
![]() .
.
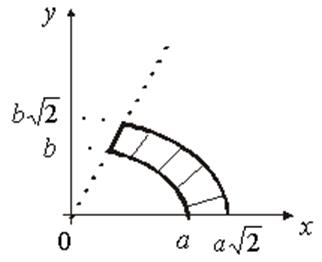 Ñ Область D ограничена линиями:
Ñ Область D ограничена линиями: ![]() – эллипс с полуосями a и b,
– эллипс с полуосями a и b, ![]() – эллипс с полуосями
– эллипс с полуосями ![]() и
и ![]() , y=0 – прямая (ось Ox),
, y=0 – прямая (ось Ox), ![]() –
прямая (рис. 14.11).
–
прямая (рис. 14.11).
|
![]() . Тогда
. Тогда 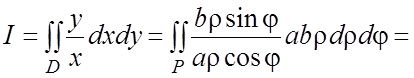
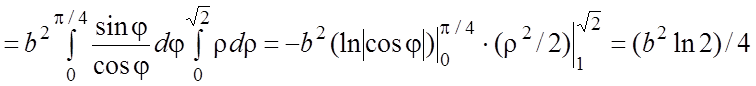 . #
. #
Задачи для самостоятельного решения
Перейти в двойном интеграле 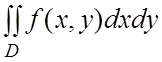 к полярным координатам
к полярным координатам ![]() и расставить пределы интегрирования в
порядке: внешнее – по j,
внутреннее - по r:
и расставить пределы интегрирования в
порядке: внешнее – по j,
внутреннее - по r:
27. D –
область, ограниченная окружностями ![]() ,
, ![]() и прямыми
и прямыми ![]() ,
, ![]() .
.
28.
D - область, являющаяся общей частью
двух кругов ![]() и
и ![]() .
.
29.
D - меньший из двух сегментов, на
которые прямая ![]() рассекает круг
рассекает круг ![]() .
.
30.
D - внутренняя часть правой петли лемнискаты
Бернулли ![]() .
.
31.
D:![]() .
.
32. D:
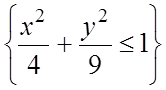 .Указание. Перейти к эллиптическим полярным координатам.
.Указание. Перейти к эллиптическим полярным координатам.
33. D
- область, ограниченная линией ![]() . Указание.
Перейти к эллиптическим полярным координатам.
. Указание.
Перейти к эллиптическим полярным координатам.
34. 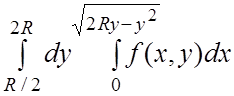 . 35.
. 35. 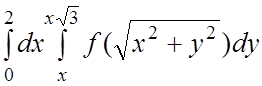 . 36.
. 36. 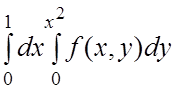 .
.
С помощью перехода к полярным координатам вычислить интегралы:
37.
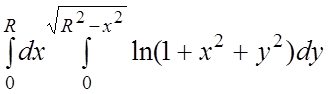 . 38.
. 38. 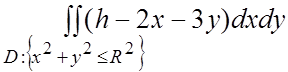 .
.
39.
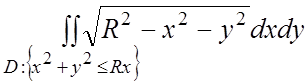 . 40.
. 40. 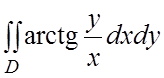 , D - часть кольца
, D - часть кольца ![]() ,
,
![]() ,
, ![]() . 41.
. 41.
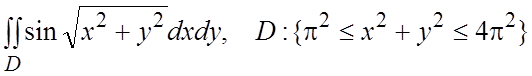 .
.
Вычислить, перейдя к эллиптическим полярным координатам, интегралы:
42.
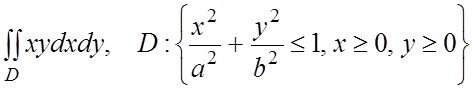 .
.
43.
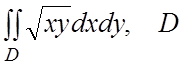 - область, ограниченная линией
- область, ограниченная линией ![]() .
.
14.3. Тройные интегралы.
14.3.1. Области в пространстве.
Определение. Область ![]() назовем правильной в направлении
Oz (правильной в направлении Ox, правильной в направлении Oy), если прямая, проходящая через
внутреннюю точку области V
параллельно оси Oz
(параллельно оси Ox, параллельно
оси Oy) пересекает границу области ровно в
двух точках.
назовем правильной в направлении
Oz (правильной в направлении Ox, правильной в направлении Oy), если прямая, проходящая через
внутреннюю точку области V
параллельно оси Oz
(параллельно оси Ox, параллельно
оси Oy) пересекает границу области ровно в
двух точках.
Область V будет правильной в направлении
Oz, если существуют функции ![]() и
и ![]() ,
заданные в S и такие,
что координаты точек, принадлежащих V, удовлетворяют условиям:
,
заданные в S и такие,
что координаты точек, принадлежащих V, удовлетворяют условиям: ![]() . Тогда символически записывают:
. Тогда символически записывают:
![]() (3.1)
(3.1)
Если, в свою очередь, область S - правильная в направлении Oy, то (см.(2.1))
![]() .
(3.2)
.
(3.2)
Если область S правильная в направлении Ox, то (см.(2.2))
![]() .
(3.3)
.
(3.3)
Задания.
1. Записать символически правильную в
направлении Oy область ![]() , если ее проекция на плоскость Oxz, в свою очередь, есть правильная
область.
, если ее проекция на плоскость Oxz, в свою очередь, есть правильная
область.
2. Записать символически правильную в
направлении Ox область ![]() , если ее проекция на плоскость Oyzесть правильная область.
, если ее проекция на плоскость Oyzесть правильная область.
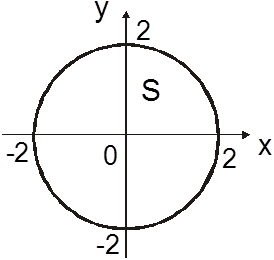
Пример 10. Область V
ограничена поверхностями ![]() и z=0.
Изобразить область и записать как правильную: а) в направлении Oz,
и z=0.
Изобразить область и записать как правильную: а) в направлении Oz,
б) в направлении Ox.
|
|
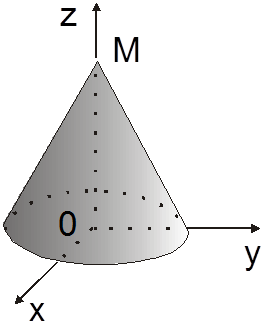 Ñ Область V - круговой конус с боковой
поверхностью, описываемой уравнением конической поверхности
Ñ Область V - круговой конус с боковой
поверхностью, описываемой уравнением конической поверхности 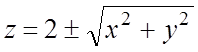 . Для точек области V имеем:
. Для точек области V имеем: 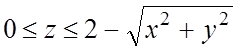 . Проекция области V на плоскость Oxy есть
. Проекция области V на плоскость Oxy есть 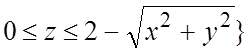 ,где
,где 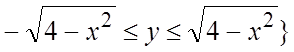 или (см.(2.2))
или (см.(2.2)) 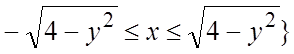 . Поэтому требуемая запись будет (см.
(3.2))
. Поэтому требуемая запись будет (см.
(3.2)) 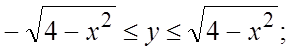
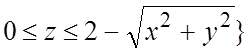 или (см. (3.3))
или (см. (3.3)) 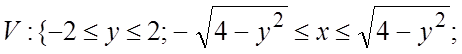
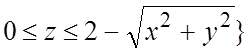 .
.
б) Рассматривая область V как правильную в направлении Ox, из уравнения ![]() имеем
имеем 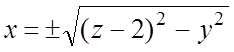 . Линии пересечения плоскости Oyz и конической поверхности находятся
из решения системы уравнений:
. Линии пересечения плоскости Oyz и конической поверхности находятся
из решения системы уравнений: ![]()
![]() ; в результате имеем
; в результате имеем 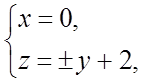 - прямые в плоскости Oyz. Итак, проекцией V на плоскость Oyz является область D - треугольник со сторонами z=y+2, z=
–y+2, z=0 (рис. 14.14), поэтому в силу (3.1)
- прямые в плоскости Oyz. Итак, проекцией V на плоскость Oyz является область D - треугольник со сторонами z=y+2, z=
–y+2, z=0 (рис. 14.14), поэтому в силу (3.1) ![]()
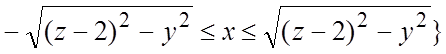 , где
, где ![]() .
.
|
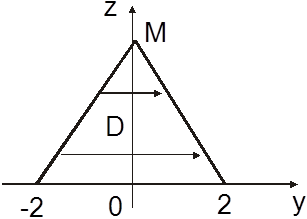 Так как область D – правильная, то рассматривая ее как правильную в направлении
Oy, имеем
Так как область D – правильная, то рассматривая ее как правильную в направлении
Oy, имеем
|
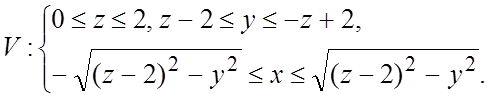 #
#
Задачи для самостоятельного решения
Изобразить указанные ниже области ![]() и
записать как правильные: а) в направлении Oz, б) в направлении Ox.
и
записать как правильные: а) в направлении Oz, б) в направлении Ox.
44.
Область Vограничена поверхностями ![]() .
.
45.
Область Vограничена поверхностями ![]() .
.
46.
Область Vограничена поверхностями ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.