1)Если ряд (6.1) –
знакочередующийся, то остаток D имеет знак своего первого члена ![]() и
и ![]() .
.
2) Если ряд (6.1) – знакоположительный, то остаток D оценивают либо с помощью остаточного члена формулы Тейлора, либо пытаются найти легко суммируемый тоже знакоположительный ряд, члены которого были бы больше членов интересующего нас остатка и оценивают остаток ряда (6.1) суммой найденного ряда.
Обычно ищут десятичное приближение числа S, в то время как члены ряда
могут и не быть десятичными дробями. При обращении их в десятичную дробь возникает новая погрешность, которую тоже нужно учесть.
Пример. Какова величина допущенной ошибки,
если приближенно положить 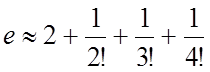 ?
?
Ñ Ошибка будет суммой знакоположительного ряда
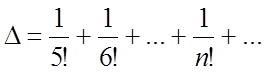 . (6.2)
. (6.2)
а) Оценим эту ошибку, заменив члены ряда (6.2) членами геометрической прогрессии, которые будут больше членов ряда (6.2)
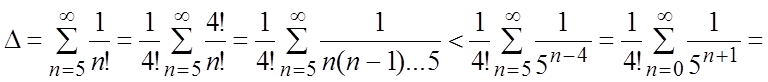
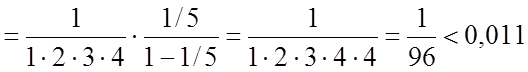 .
.
б) оценим эту же ошибку с помощью остаточного члена формулы Маклорена
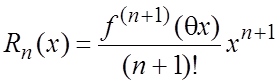 . В
нашем случае
. В
нашем случае ![]()
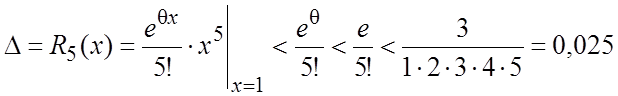 . #
. #
Пример. Вычислить 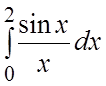 с
точностью до 0,001 (предполагаем, что
с
точностью до 0,001 (предполагаем, что 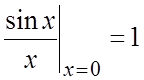 ).
).
Ñ 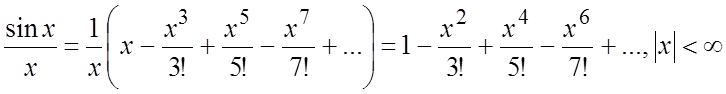 .
.
Проинтегрируем полученное разложение на [0, 2]:
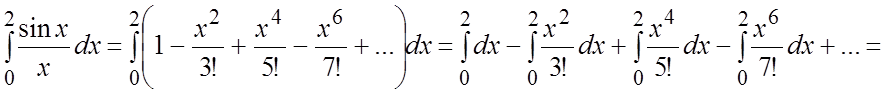
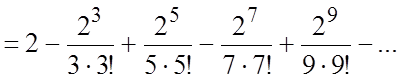 (6.3)
(6.3)
Получили знакочередующийся ряд. Если
для вычисления интеграла 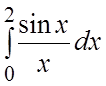 взять 4 члена ряда
(6.3), то ошибка
взять 4 члена ряда
(6.3), то ошибка ![]() , которая получается за счет
отбрасывания членов ряда, начиная с пятого, не будет превосходить первого из
отброшенных членов, т.е.
, которая получается за счет
отбрасывания членов ряда, начиная с пятого, не будет превосходить первого из
отброшенных членов, т.е. 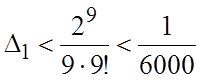 . Вычисления нужно
вести с 4 знаками после запятой, тогда ошибка
. Вычисления нужно
вести с 4 знаками после запятой, тогда ошибка ![]() ,
которая получается при обращении II, III, и IV членов ряда (6.3) в десятичные дроби будет меньше
,
которая получается при обращении II, III, и IV членов ряда (6.3) в десятичные дроби будет меньше 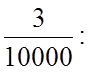
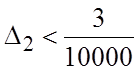 .
Общая ошибка
.
Общая ошибка ![]() .
. 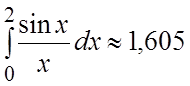 .
Результат округлен до III
знака после запятой. #
.
Результат округлен до III
знака после запятой. #
Пример. Найти общее решение
дифференциального уравнения ![]() в виде степенного
ряда.
в виде степенного
ряда.
Ñ Т.к. x = 0 не является особой точкой для данного дифференциального уравнения, то решение его можно искать в виде ряда
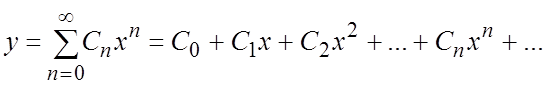 (6.4)
(6.4)
Продифференцируем ряд (6.4) дважды:
![]()
![]()
![]() .
(6.5)
.
(6.5)
Подставим в уравнение вместо ![]() и
и ![]() соответственно
ряды (6.4) и (6.5):
соответственно
ряды (6.4) и (6.5):
![]()
![]()
![]()
![]() или
или
![]()
![]() .
.
Приравнивая коэффициенты
при всех степенях x
к нулю, получим: 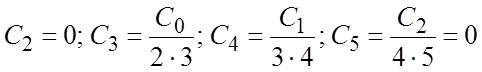 .
.
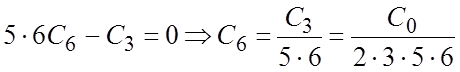 ,
, 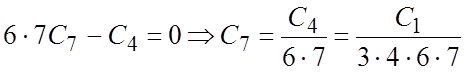 и т.д.
и т.д.
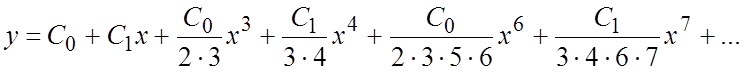
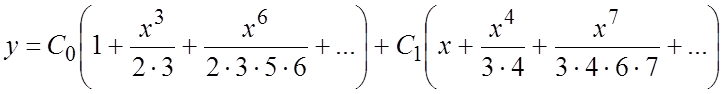 #
#
Пример. Применяя метод последовательных дифференцирований, найти 5 членов разложения в ряд решения дифференциального уравнения
![]() при
начальных условиях
при
начальных условиях ![]() .
.
Ñ Точка x = 0 не является особой точкой данного дифференциального уравнения, поэтому решение можно искать в виде:
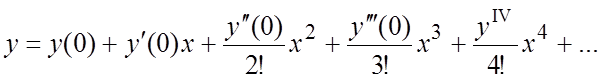 (6.6)
(6.6)
(разложение в окрестности x = 0!). Здесь ![]() .
.
Из уравнения ![]() .
.
Из уравнения ![]()
![]() ,
,
![]() ,
,
![]() .
.
Подставим в (6.6) ![]()
![]() :
: 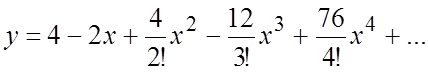 или
или 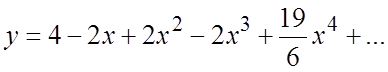 #
#
Задачи для самостоятельного решения
57. Вычислить приближенное значение ![]() , взяв 3 члена разложения в ряд Маклорена
функции
, взяв 3 члена разложения в ряд Маклорена
функции![]() , оценить погрешность.
, оценить погрешность.
58. Вычислить приближенное значение ![]() , взяв 3 члена разложения в ряд Маклорена
функции
, взяв 3 члена разложения в ряд Маклорена
функции ![]() , оценить погрешность.
, оценить погрешность.
Вычислить приближенно с указанной степенью точности D.
59. 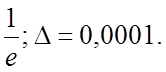 60.
60.
![]() 61.
61. ![]()
62. ![]() 63.
63. ![]() . 64.
. 64. ![]()
Следующие интегралы вычислить с точностью до 0,001.
65. 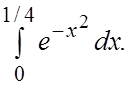 66.
66.
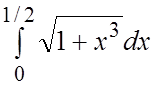 . 67.
. 67. 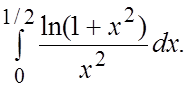 68.
68.
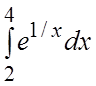 .
.
69. Вычислить приближенно 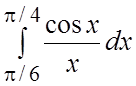 , взяв
3 первых члена разложения подынтегральной функции в ряд. Оценить погрешность.
, взяв
3 первых члена разложения подынтегральной функции в ряд. Оценить погрешность.
70. Найти 6 первых членов разложения в степенной ряд
решения дифференциального уравнения ![]() , удовлетворяющего
начальным условиям:
, удовлетворяющего
начальным условиям:
![]() .
.
71. Записать в виде степенного ряда частное решение
дифференциального уравнения ![]() .
.
Записать в виде степенного ряда общее решение дифференциального уравнения.
72. ![]()
![]() (шесть
первых членов)
(шесть
первых членов)
73. ![]() .
74.
.
74. ![]() .
.
75. Найти 3 члена разложения в ряд частного решения уравнения
![]()
1.[-1; 1] 2. (-1; 1) 3.
![]() 4. (-2;2) 5.
4. (-2;2) 5.![]() 6.
6. ![]()
7. 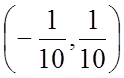 8. {0} 9.
8. {0} 9. 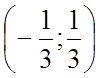 10.
10. ![]() 11.
11.
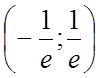 12.
12.![]()
13.[-6;-4]14.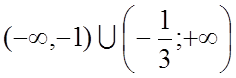 15.
15.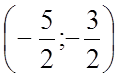 16.
16.![]()
17. 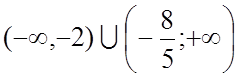 18.
18. 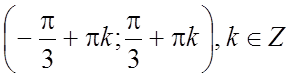 19.
19. 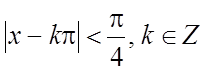
25. 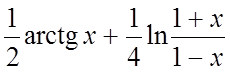 26.
26. ![]() 27.
27. 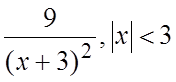
28. 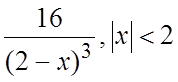 . 29.
. 29. 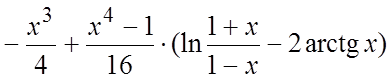 30.
30.
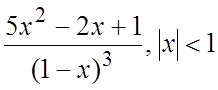
31. a) 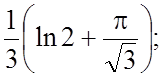 б)
б) 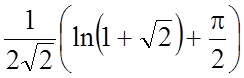 33.
33.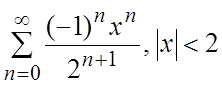
34. 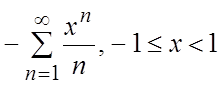 35.
35.
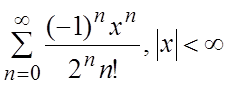 36.
36. 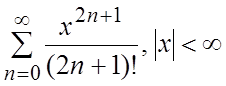
37. 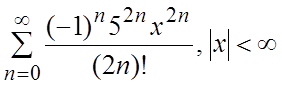 38.
38.
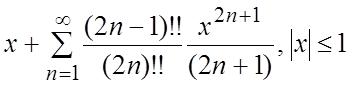
39. 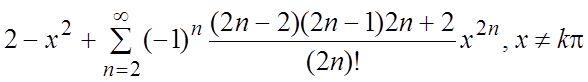
40.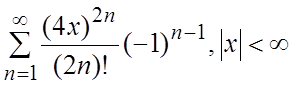 41.
41. 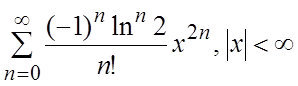
42. 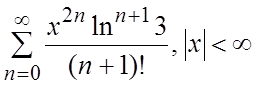 43.
43.
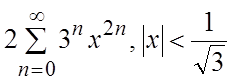
44. 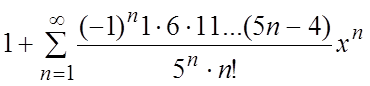 45.
45.
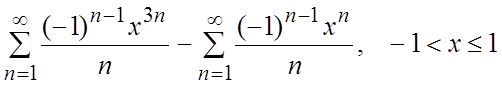
46. 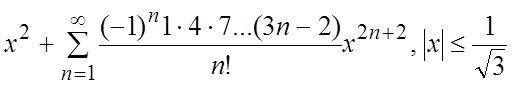
47.  48.
48.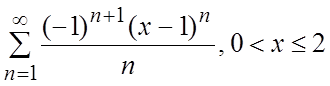
49. 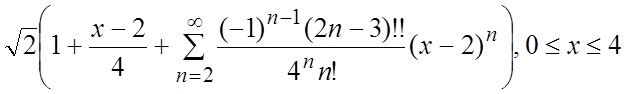
50. 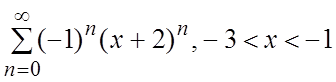 51.
51.
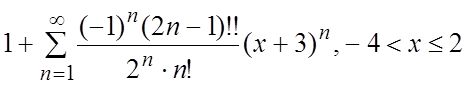
52. 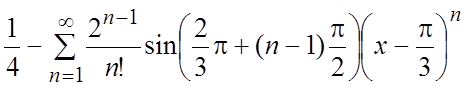 ,
, ![]() 53.
53.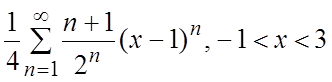
54. 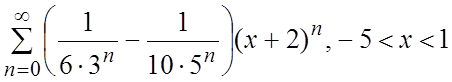 55.
55.
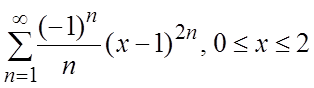
56. 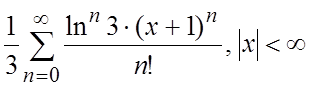 57. 1,39, D=0,01 58. 0,3090, D=0,0001 59. 0,3679 60.
0,9848 61. 4,309 62. 3,079 63. 1,609 64.
3,14159 65. 0,245 66. 0,508
57. 1,39, D=0,01 58. 0,3090, D=0,0001 59. 0,3679 60.
0,9848 61. 4,309 62. 3,079 63. 1,609 64.
3,14159 65. 0,245 66. 0,508
67. 0,481 68. 2,835 69. 0,3230, D=0,0001
70. 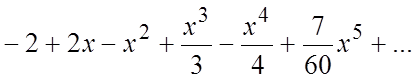
71. 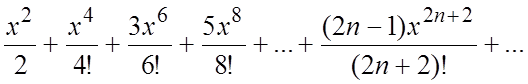
72. 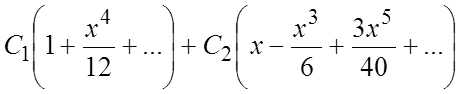
73. 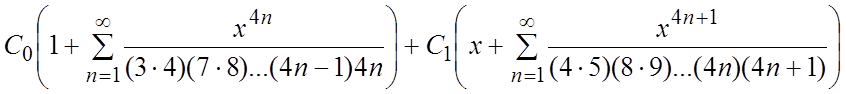
74. 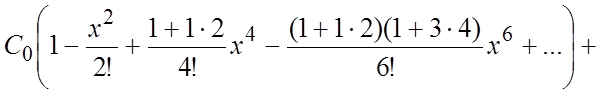
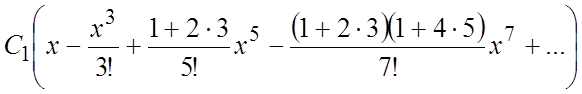
75. 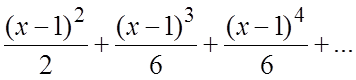
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.