![]()
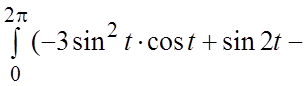
![]()
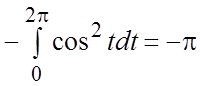 .
.
15.1.4. Дивергенция векторного поля
Интегральные характеристики – поток и линейный интеграл – характеризуют векторное поле “в целом”. Количественную характеристику поля в каждой точке дают, вводимые ниже, дифференциальные характеристики. Введем понятие дивергенции.
Окружим произвольную точку M поверхностью (S) произвольной формы (например, сферой достаточно малого радиуса). Пусть (V) – объем, заключенный внутри поверхности (S).
Определение. Конечный предел отношения потока поля через
поверхность (S) к объему, заключенному внутри
нее при стягивании поверхности к точке M и
стремлении объема V к нулю называется
дивергенцией векторного поля ![]() в точке M:
в точке M:
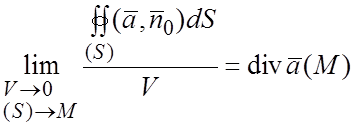 (1.10¢)
(1.10¢)
Замечание. Определение (1.10) есть инвариантное (не зависящее от системы координат) определение дивергенции.
Дивергенция
характеризует отнесенную к единице объема мощность потока векторного поля,
“исходящего” из точки M, то есть мощность
источника (при ![]() ), или стока (при
), или стока (при ![]() ), находящегося в точке M.
), находящегося в точке M.
В декартовой системе координат дивергенция вычисляется по формуле
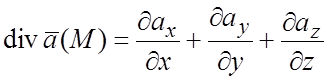 . (1.10)
. (1.10)
Свойства
дивергенции. Пусть ![]() и
и ![]() -
векторные поля,
-
векторные поля, ![]() - скалярная функция. Тогда:
- скалярная функция. Тогда:
1) ![]() ; 2)
; 2) ![]() . (1.11)
. (1.11)
С учетом формулы (1.10) перепишем формулу Гаусса-Остроградского (1.6)
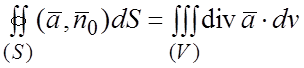 (1.12)
(1.12)
- поток
векторного поля ![]() через замкнутую поверхность (S) равен тройному интегралу по объему (V), заключенному внутри этой поверхности от дивергенции
поля.
через замкнутую поверхность (S) равен тройному интегралу по объему (V), заключенному внутри этой поверхности от дивергенции
поля.
Пример 1.
Вычислить ![]() .
.
Решение. 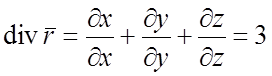 .
.
Пример 2.
Вычислить ![]() , где u(M) – скалярная функция,
, где u(M) – скалярная функция, ![]()
![]() - векторная функция.
- векторная функция.
Решение. По
формуле (1.10) находим: 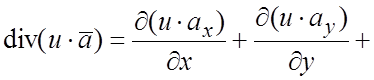
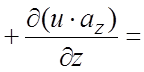
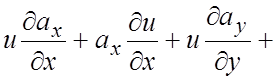
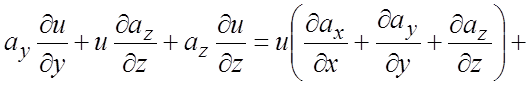
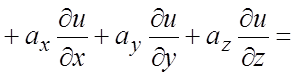
![]() .
.
Пример 3. Используя теорему Гаусса-Остроградского (1.12), найти
поток векторного поля ![]() через всю поверхность (S) тела (V):
через всю поверхность (S) тела (V):
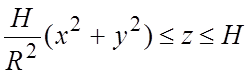 в направлении внешней нормали.
в направлении внешней нормали.
Решение. Имеем ![]() . Поэтому
. Поэтому 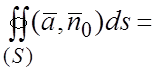 =
=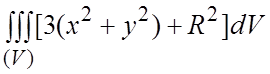 . Для вычисления тройного интеграла
перейдем к цилиндрическим координатам. Уравнение поверхности примет вид
. Для вычисления тройного интеграла
перейдем к цилиндрическим координатам. Уравнение поверхности примет вид ![]() ,
, 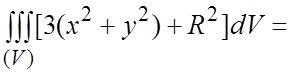
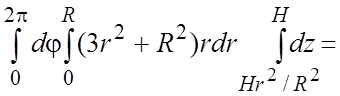
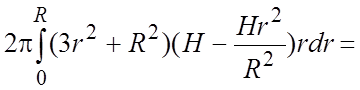 =
=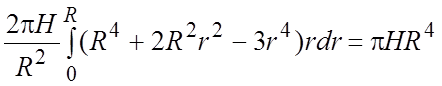 .
.
15.1.5. Ротор (вихрь) векторного поля
Пусть
поле ![]() - дифференцируемое поле (то есть проекции
вектора поля на оси координат являются дифференцируемыми функциями).
- дифференцируемое поле (то есть проекции
вектора поля на оси координат являются дифференцируемыми функциями).
Определение. Вихрем векторного поля ![]() (обозначается
rot
(обозначается
rot![]() ) называется вектор,
проекция которого на произвольный вектор
) называется вектор,
проекция которого на произвольный вектор ![]() определяется
как предел отношения циркуляции поля
определяется
как предел отношения циркуляции поля ![]() по некоторому контуру (L), содержащему точку M, и
лежащему в плоскости, перпендикулярной вектору
по некоторому контуру (L), содержащему точку M, и
лежащему в плоскости, перпендикулярной вектору ![]() , к
площади области, ограниченной этим контуром, при условии, что этот контур
стягивается в точку M, а площадь области (S) стремится к нулю:
, к
площади области, ограниченной этим контуром, при условии, что этот контур
стягивается в точку M, а площадь области (S) стремится к нулю:
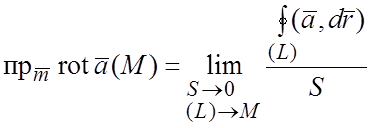 .
(1.13)
.
(1.13)
В трехмерном пространстве ![]() через декартовы прямоугольные координаты
вектора
через декартовы прямоугольные координаты
вектора ![]() выражается следующим образом:
выражается следующим образом:
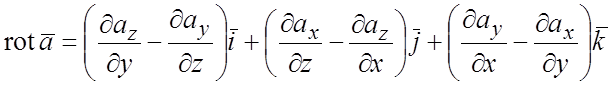 , (1.14)
, (1.14)
или в удобной для запоминания символической форме
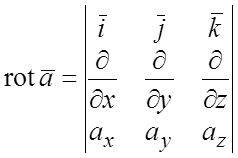 .
(1.15)
.
(1.15)
Теорема Стокса. Пусть координаты вектора ![]() +
+![]()
![]() непрерывны и имеют
непрерывные частные производные. Тогда циркуляция векторного поля
непрерывны и имеют
непрерывные частные производные. Тогда циркуляция векторного поля ![]() по замкнутому контуру (L) равна потоку вихрей поля через произвольную
поверхность (S), натянутую на этот контур:
по замкнутому контуру (L) равна потоку вихрей поля через произвольную
поверхность (S), натянутую на этот контур:
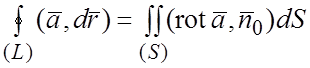 . (1.16)
. (1.16)
Предполагается, что ориентация контура (L) и поверхности (S) согласованы: при положительном обходе контура нормаль направлена от “ног к голове”.
Свойства ротора: 1) ![]() ; 2)
; 2) ![]() .
.
Определение.
Векторное поле ![]() называется безвихревым в данной
области (V), если
называется безвихревым в данной
области (V), если ![]() .
.
Пример 1.
Найти ротор поля вектора напряженности магнитного поля 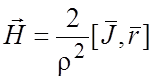 .
.
Решение.Вектор
![]() в координатной форме:
в координатной форме: 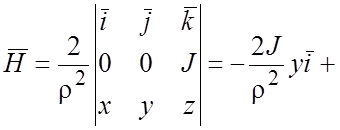
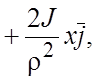
![]() . Вычислим ротор по формуле (1.15):
. Вычислим ротор по формуле (1.15):
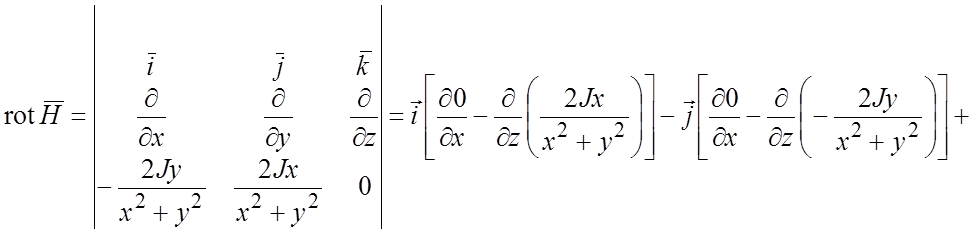
+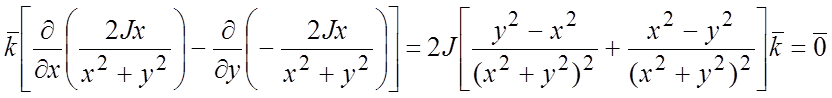 -
-
- поле напряженности ![]() - безвихревое поле.
- безвихревое поле.
Пример 2. Вычислить циркуляцию вектора ![]() по
контуру
по
контуру ![]() 1)непосредственно, 2)по теореме Стокса.
1)непосредственно, 2)по теореме Стокса.
|
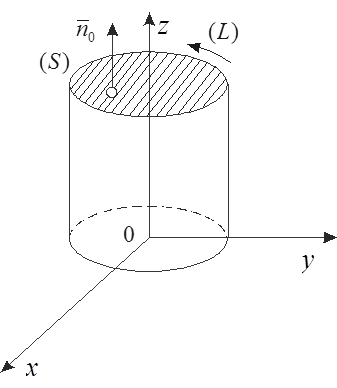 Решение. 1)Контур (L) – окружность радиуса
Решение. 1)Контур (L) – окружность радиуса
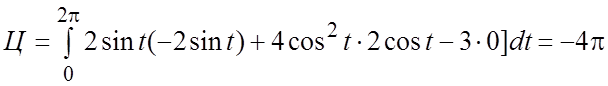 .
2)Для вычисления циркуляции по теореме Стокса выберем какую-нибудь поверхность
(S), натянутую на контур (L).Естественно
в качестве (S) взять круг, имеющий линию (L) своей границей. Согласно выбранной ориентации контура
нормаль
.
2)Для вычисления циркуляции по теореме Стокса выберем какую-нибудь поверхность
(S), натянутую на контур (L).Естественно
в качестве (S) взять круг, имеющий линию (L) своей границей. Согласно выбранной ориентации контура
нормаль 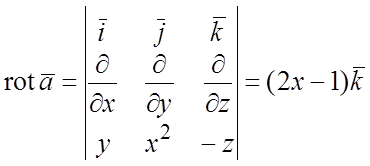 .
.
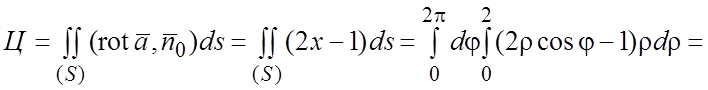
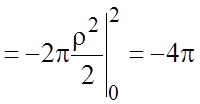 .
.
Задачи для самостоятельного решения
Найти векторные линии плоских векторных полей:
1.![]() ;
2.
;
2. ![]() ; 3.
; 3. ![]() ; 4.
; 4.![]() ;
;
5.![]() .
.
Найти векторные линии:
6. ![]() ; 7.
; 7. ![]() , где
, где ![]() ;
;
8. 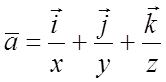 ; 9.
; 9.![]() ,
, ![]() ;
;
10.![]() ; 11.
; 11.![]() ; 12.
; 12.![]() ;
;
13.![]() , где
, где ![]() -
постоянные векторы.
-
постоянные векторы.
Найти векторные линии, проходящие через заданную точку:
14.![]() ,
,
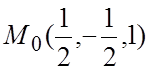 ; 15.
; 15.![]() ,
, ![]() .
.
Вычислить поток векторного поля, используя поверхностный интеграл первого рода:
16. ![]() , (S):
верхняя сторона треугольника, ограниченного плоскостями
, (S):
верхняя сторона треугольника, ограниченного плоскостями ![]() ,
,
![]() .
.
17. ![]() , (S):
внешняя сторона параболоида
, (S):
внешняя сторона параболоида ![]() , ограниченного
плоскостью
, ограниченного
плоскостью ![]() ;
;
18. ![]() ,
, ![]() :
боковая поверхность кругового цилиндра
:
боковая поверхность кругового цилиндра 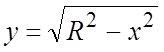 , ограниченного
плоскостями
, ограниченного
плоскостями ![]() ;
;
19. ![]() , (S):
внешняя сторона части параболоида
, (S):
внешняя сторона части параболоида ![]() , расположенной в
первом октанте;
, расположенной в
первом октанте;
20. ![]() , (S):
полная поверхность конуса
, (S):
полная поверхность конуса ![]() , ограниченного
плоскостью
, ограниченного
плоскостью ![]() ;
;
21. ![]() , (S):
замкнутая поверхность, ограниченная параболоидом
, (S):
замкнутая поверхность, ограниченная параболоидом ![]() и
плоскостью z = 0;
и
плоскостью z = 0;
22. ![]() , (S):
полная поверхность пирамиды, ограниченной плоскостями
, (S):
полная поверхность пирамиды, ограниченной плоскостями ![]() ,
,
![]() ,
, ![]() ,
, ![]() ;
;
23. ![]() , (S): сфера
, (S): сфера
![]() .
.
Вычислить поток, используя метод проектирования на все три координатные плоскости.
24. ![]() ,
(S): верхняя сторона круга, вырезанного конусом
,
(S): верхняя сторона круга, вырезанного конусом 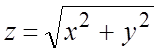 на плоскости
на плоскости ![]()
25. ![]() ,
(S): верхняя сторона треугольника, полученного
пересечением плоскости
,
(S): верхняя сторона треугольника, полученного
пересечением плоскости ![]() с координатными
плоскостями;
с координатными
плоскостями;
26. ![]() , (S):
часть плоскости
, (S):
часть плоскости ![]() , ограниченная окружностью
, ограниченная окружностью ![]() , в направлении орта
, в направлении орта ![]() .
.
Определить поток поля, используя формулу Гаусса-Остроградского:
27. ![]() ,
(S): произвольная кусочно гладкая замкнутая
поверхность;
,
(S): произвольная кусочно гладкая замкнутая
поверхность;
28. ![]() , (S):
поверхность куба
, (S):
поверхность куба ![]() ,
, ![]() ,
, ![]() ;
;
29. ![]() ,
(S): сфера
,
(S): сфера ![]() ;
;
30. ![]() , (S):
часть параболоида
, (S):
часть параболоида ![]() , отсекаемая плоскостью
, отсекаемая плоскостью ![]() ; в отрицательную сторону оси Ox;
; в отрицательную сторону оси Ox;
31.![]() , (S):
поверхность тела
, (S):
поверхность тела ![]() ,
, ![]() ,
, ![]() ,
,
![]() ;
;
32. ![]() , (S):
поверхность тела
, (S):
поверхность тела ![]() ,
, ![]() ;
;
33. ![]() , (S):
, (S):
![]() ;
;
34.![]() ;
;
35. ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.