Глава4. Дифференциальное исчисление функции одной переменной
4.1. Производная. Дифференцирование явно заданных функций
Пусть ![]() есть приращение функции
есть приращение функции ![]() в точке
в точке ![]() ,
соответствующее приращению аргумента
,
соответствующее приращению аргумента ![]() . Производной функции
. Производной функции
![]() в точке
в точке ![]() называется
предел
называется
предел 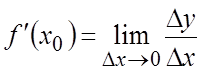 . Числа
. Числа 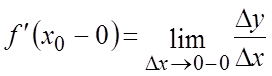 и
и 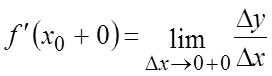 называются
соответственно левой и правой производными функции
называются
соответственно левой и правой производными функции ![]() в точке
в точке ![]() .
Необходимым и достаточным условием существования
.
Необходимым и достаточным условием существования ![]() является
существование и совпадение
является
существование и совпадение ![]() и
и ![]() . Процесс нахождения производной называется
дифференцированием.
. Процесс нахождения производной называется
дифференцированием.
1. ![]() , где С
- const. 2.
, где С
- const. 2. 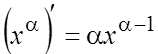 ,
, ![]() .
.
3. 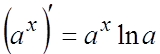 ,
, ![]() ;
; 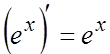 . 4.
. 4. 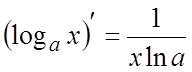 ,
, ![]() ;
; 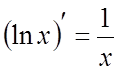 .
.
5. ![]() . 6.
. 6.![]() . 7.
. 7. 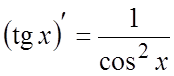 . 8.
. 8.
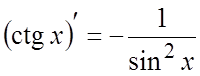 .
.
9. 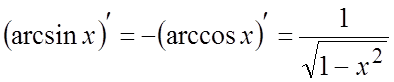 .
10.
.
10. 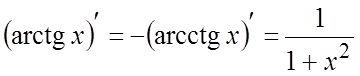 .
.
11. ![]() . 12.
. 12.
![]() . 13.
. 13. 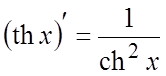 .
14.
.
14. 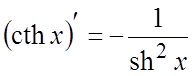 .
.
Правила дифференцирования функций. Пусть ![]() и
и ![]() дифференцируемые функции. Тогда:
дифференцируемые функции. Тогда:
1. ![]() . 2.
. 2. ![]() . 3.
. 3. 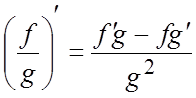 , где
, где ![]() .
.
Пример. Найти производную функции ![]() .
.
Ñ Полагая ![]() и
и 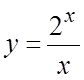 , имеем
, имеем 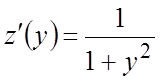 и
и 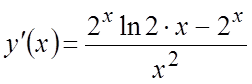 .
.
Тогда получаем: 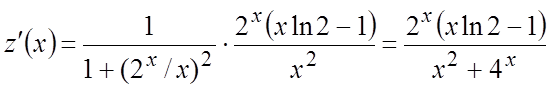 . #
. #
Правило дифференцирования сложной функции справедливо для любого конечного числа композиций основных элементарных функций.
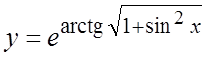 .
.Ñ Используя таблицу производных и
правила дифференцирования, получаем: 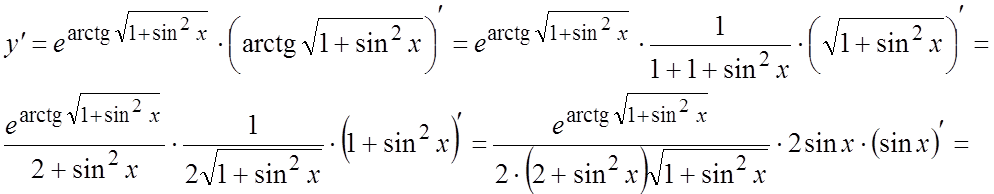 =
=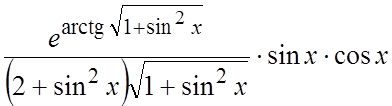 . #
. #
Производная от логарифма
функции ![]() , т.е.
, т.е. ![]() называется
логарифмической производной, а операция дифференцирования – логарифмическим
дифференцированием. Применение логарифмирования часто упрощает взятие
производной, а в случае степенно-показательной функции оно необходимо.
называется
логарифмической производной, а операция дифференцирования – логарифмическим
дифференцированием. Применение логарифмирования часто упрощает взятие
производной, а в случае степенно-показательной функции оно необходимо.
Ñ Логарифмируя, получим ![]()
![]() .
Находим производные левой и правой частей равенства:
.
Находим производные левой и правой частей равенства: 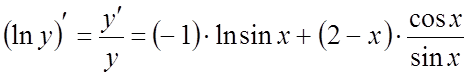 .
.
Тогда ![]() . #
. #
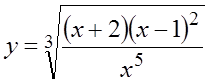 .
.Ñ 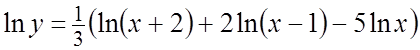 . Дифференцируя
обе части равенства, получим:
. Дифференцируя
обе части равенства, получим: 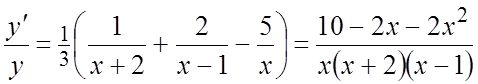 ,
,
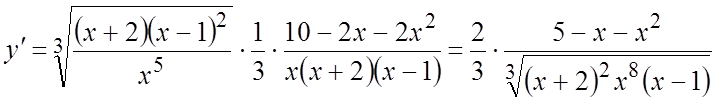 . #
. #
1. ![]() . 2.
. 2. 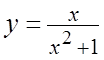 . 3.
. 3. 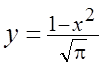 . 4.
. 4.
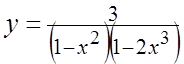 . 5.
. 5. 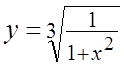 .
.
6. 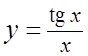 . 7.
. 7. 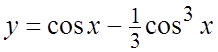 . 8.
. 8. 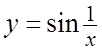 . 9.
. 9. ![]() .
.
10. ![]() . 11.
. 11.
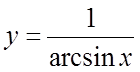 . 12.
. 12. 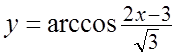 .
13.
.
13. ![]() .
.
14. 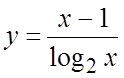 .
15.
.
15. ![]() . 16.
. 16. 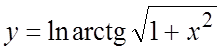 . 17.
. 17.
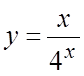 .
.
18. 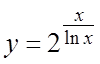 . 19.
. 19.
![]() . 20.
. 20. 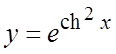 . 21.
. 21.
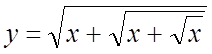 . 22.
. 22. 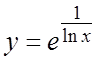 . 23.
. 23. ![]() . 24.
. 24. ![]() .
25.
.
25. 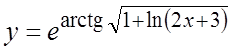 . 26.
. 26.![]() .
.
27. 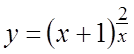 . 28.
. 28.
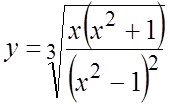 . 29.
. 29. 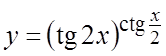 . 30.
. 30. 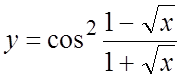 .
.
4.2. Дифференцирование функций, заданных неявно или параметрически
Функция ![]() называется заданной неявно
уравнением
называется заданной неявно
уравнением ![]() на некотором множестве
на некотором множестве ![]() , если
, если ![]() ,
, ![]() . Для нахождения производной функции
. Для нахождения производной функции ![]() необходимо продифференцировать по
необходимо продифференцировать по ![]() обе части уравнения
обе части уравнения ![]() и
затем полученное уравнение разрешить относительно
и
затем полученное уравнение разрешить относительно ![]() .
.
ÑДифференцируя по ![]() обе части равенства
обе части равенства ![]() получим:
получим:
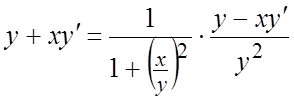 ;
; 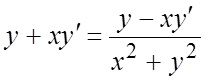 ;
;
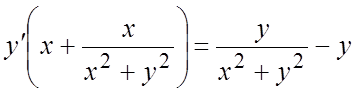 ,
, 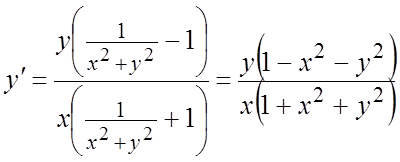 . #
. #
Пусть заданы функции ![]() ,
, ![]() ,
, ![]() и пусть на интервале
и пусть на интервале ![]() функция
функция ![]() имеет
обратную
имеет
обратную ![]() . Тогда можно определить функцию
. Тогда можно определить функцию ![]() , которая называется параметрически
заданной.
, которая называется параметрически
заданной.
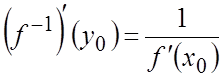 .
Более простая форма записи для произвольной точки
.
Более простая форма записи для произвольной точки 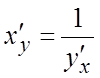 . Применяя теорему 1,
получим: для функции, заданной параметрически:
. Применяя теорему 1,
получим: для функции, заданной параметрически: 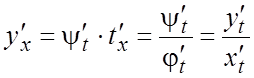
Ñ Так как ![]() ,
, ![]() , то
, то 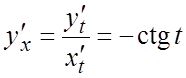 . #
. #
Найти производные от ![]() по
по ![]() для
неявно заданных функций.
для
неявно заданных функций.
31. ![]() . 32.
. 32.
![]() . 33.
. 33. ![]() .
.
34. ![]() .
35.
.
35. ![]() . 36.
. 36. ![]() . 37.
. 37.
![]() .
.
Найти производные от ![]() по
по ![]() для
функций заданных параметрически.
для
функций заданных параметрически.
38. ![]() ,
,![]() . 39.
. 39. ![]() .
.
40. 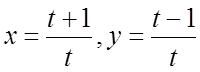 .
41.
.
41. 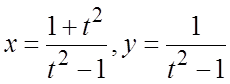 . 42.
. 42. 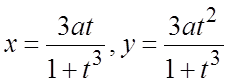 .
.
4.3. Производные высших порядков.
Производной второго
порядка от функции ![]() называется производная
от ее первой производной, т.е.
называется производная
от ее первой производной, т.е. ![]() .Соответственно производной
n-ного порядка называется производная от (n-1) - ой производной, т.е.
.Соответственно производной
n-ного порядка называется производная от (n-1) - ой производной, т.е. 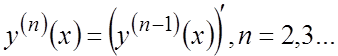
Ñ 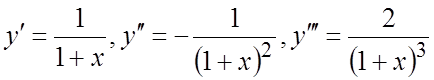 ,
,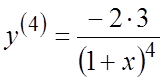 . Продолжая дифференцирование функции, получим:
. Продолжая дифференцирование функции, получим:
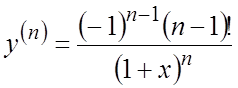 . #
. #
Если функции ![]() и
и
![]() имеют производные до n-ного порядка включительно, то
справедлива формула Лейбница:
имеют производные до n-ного порядка включительно, то
справедлива формула Лейбница:
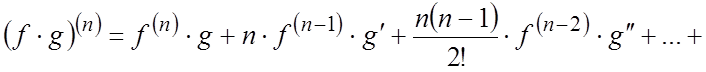
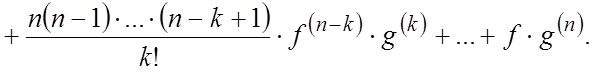
Пример. Найти
производную 5-го порядка от функции ![]() .
.
Ñ 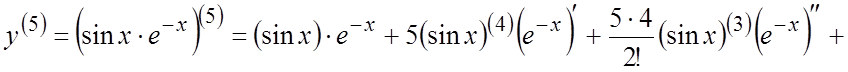
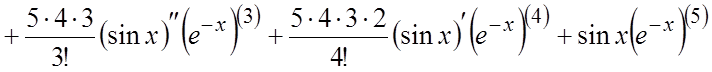 .
.
Имеем: ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, 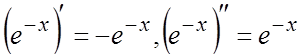 ,
, 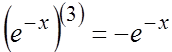 ,
, 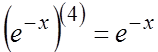 ,
,
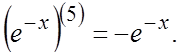 Подставляя
полученные значения производных, находим:
Подставляя
полученные значения производных, находим:
![]()
![]()
![]() . #
. #
Ñ Дифференцируя уравнение по ![]() , получаем
, получаем 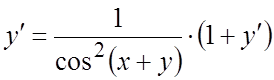 .
.
Отсюда 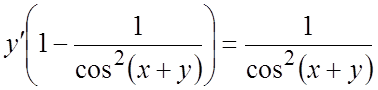 , или
, или ![]() .
.
Заменим ![]() на
на ![]() из условия:
из условия: 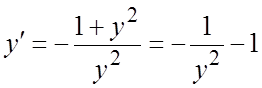 .
Дифференцируя последнее уравнение по
.
Дифференцируя последнее уравнение по ![]() , имеем:
, имеем: 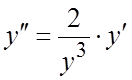 . Используя найденное для
. Используя найденное для ![]() выражение, получаем
выражение, получаем 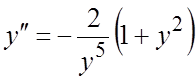 . #
. #
Для функции ![]() ,
заданной параметрически,
,
заданной параметрически, ![]() , производная второго
порядка находится по формуле
, производная второго
порядка находится по формуле 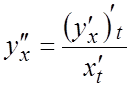 . Производная порядка n определяется следующим образом:
. Производная порядка n определяется следующим образом: 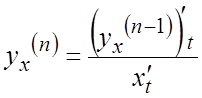 .
.
Пример. Найти производную второго
порядка от функции, заданной параметрически: ![]() .
.
Ñ Найдем первую
производную: 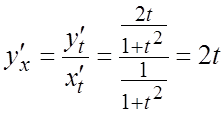 . Тогда
. Тогда 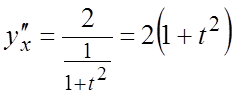 .#
.#
Задачи для самостоятельного решения
43. ![]() 44.
44. ![]()
45. ![]() 46.
46. ![]() 47.
47.
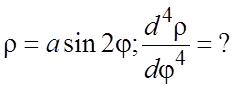
48. ![]() 49.
49. 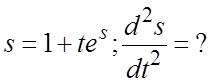 50.
50.
![]() Найти
Найти ![]() .
.
51. 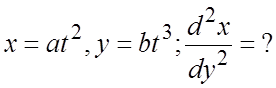 52.
52. 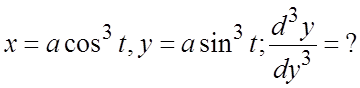
53. 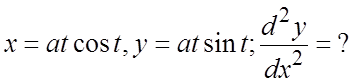
54. Применить формулу Лейбница для вычисления производной: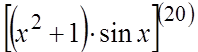 .
.
4.4. Геометрический и механический смысл производной
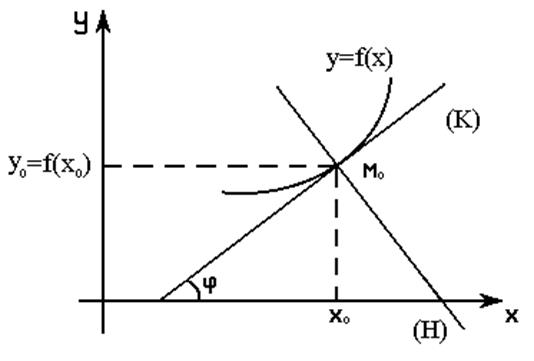
|
![]() .
(Рис. 1).
.
(Рис. 1).
|
Нормалью к графику функции ![]() в точке
в точке ![]() называется
прямая, проходящая через точку
называется
прямая, проходящая через точку ![]() перпендикулярно
касательной в этой точке.
перпендикулярно
касательной в этой точке.
Ее уравнение: 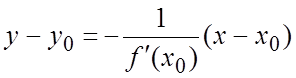 .
.
Углом между кривыми в их общей точке называется угол между касательными, проведенными к кривым в этой точке.
Механический смысл
производной: Если
закон движения материальной точки описывается функцией ![]() ,
то
,
то ![]() есть скорость, а
есть скорость, а ![]() -
ускорение этой точки в момент времени t.
-
ускорение этой точки в момент времени t.
Пример. Написать уравнения касательной и
нормали к графику функции 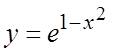 в точке
в точке ![]() .
.
Ñ 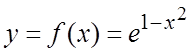 ,
, 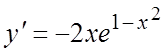 . Тогда
. Тогда ![]() ,
, ![]() .Составим уравнение касательной
.Составим уравнение касательной ![]() и нормали
и нормали ![]() к
графику .
к
графику . ![]() :
: ![]() ,
, ![]() :
: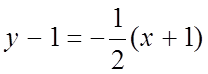 или
или ![]() :
: ![]() ,
, ![]() :
: ![]() .#
.#
Пример. Написать уравнение касательной к
кривой ![]() ,
, ![]() в точке
в точке
![]() .
.
Ñ Вычислим 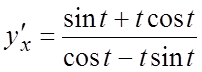 .
Тогда
.
Тогда 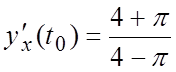 ,
, 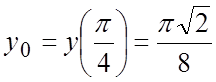 ,
,
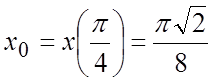 .
Уравнение касательной имеет вид:
.
Уравнение касательной имеет вид: 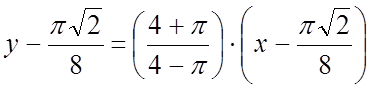 .#
.#
Пример.
Найти угол под которым пересекаются
кривые 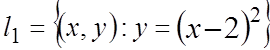 и
и ![]()
Ñ Найдем точки пересечения кривых ![]() и
и ![]() . Из
равенства
. Из
равенства ![]() находим точки пересечения
находим точки пересечения ![]() ,
, ![]() .
Вычислим угловые коэффициенты
.
Вычислим угловые коэффициенты ![]() и
и ![]() касательных к кривым
касательных к кривым ![]() и
и ![]() в точке
в точке
![]() .
. 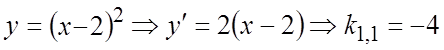 ,
, 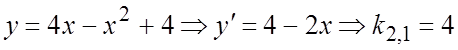
Угол ![]() между
касательными определяем по формуле
между
касательными определяем по формуле
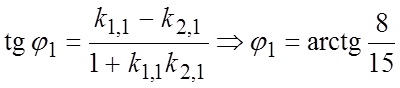 . В точке
. В точке ![]() имеем
соответственно
имеем
соответственно ![]() и
и ![]() . Тогда
. Тогда ![]() и
и ![]() . #
. #
Пример. Тело массой 4 движется прямолинейно
по закону ![]() . Определить кинетическую энергию тела в
момент времени
. Определить кинетическую энергию тела в
момент времени ![]() .
.
Ñ Найдем скорость ![]() в момент времени
в момент времени ![]() .
. ![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.