Полагая ![]() , находим
, находим ![]() , так
что находим
, так
что находим ![]() , так что
, так что 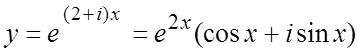 ,
, ![]() . Отделяя действительные и мнимые части,
получим два вещественных линейно независимых частных решения
. Отделяя действительные и мнимые части,
получим два вещественных линейно независимых частных решения ![]()
![]() ;
; ![]() . Общее решение (1):
. Общее решение (1): ![]() ,
, ![]() .
.
Пример 3. Найти общее решение системы
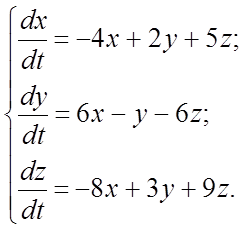 (1)
(1)
Характеристическое уравнение
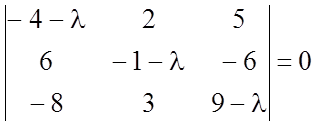 или
или ![]()
имеет корни ![]() . Найдем частное решение, соответствующее
простому корню
. Найдем частное решение, соответствующее
простому корню ![]() . Числа
. Числа ![]() определяем
из системы
определяем
из системы ![]() ,
, ![]() .
Сложив эти уравнения, придем к равенству
.
Сложив эти уравнения, придем к равенству ![]() .
Полагая
.
Полагая ![]() , найдем
, найдем ![]() , так
что искомое частное решение:
, так
что искомое частное решение: ![]()
![]() ,
, ![]() .
Построим два линейно независимых частных решения, соответствующих кратному
корню
.
Построим два линейно независимых частных решения, соответствующих кратному
корню ![]() . Согласно формуле (5.13) ему отвечает
решение вида
. Согласно формуле (5.13) ему отвечает
решение вида ![]() (2)
(2)
Коэффициенты ![]() определяются подстановкой (2) в систему
(1). Подставляя (2) в (1) и сокращая на
определяются подстановкой (2) в систему
(1). Подставляя (2) в (1) и сокращая на ![]() ,
получим систему
,
получим систему
![]() ;
;
![]() ;
;
![]() .
.
Приравнивая
коэффициенты при t и свободные члены, получим
систему
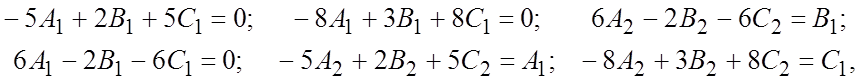
откуда ![]() , причем
, причем ![]() и
и ![]() произвольны.
произвольны.
Решение (2) принимает вид: ![]()
![]() ,
, ![]() .
.
В качестве линейно независимых частных решений, соответствующих корню ![]() можно взять
можно взять ![]()
![]() ,
, ![]() .
.
Общее решение системы (1): ![]() ,
, ![]()
![]() .
.
Пример 4. Найти общее решение СНЛДУ ![]() ,
, ![]() (1) методом вариации произвольных
постоянных.
(1) методом вариации произвольных
постоянных.
Решение. Соответствующая однородная система рассмотрена в примере
1. Общее решение системы (1) ищем в виде (5.8): ![]() ,
, ![]() (2). Функции
(2). Функции ![]() и
и ![]() находим из системы (5.9):
находим из системы (5.9):
![]() ,
, ![]() ,
откуда
,
откуда ![]()
![]() и
и ![]()
![]() . Запишем общее решение
(1):
. Запишем общее решение
(1): ![]() ,
, ![]() .
.
Задачи для самостоятельного решения
Проинтегрировать следующие системы последовательным интегрированием или методом исключения:
286. 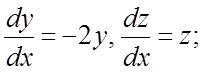 287.
287.
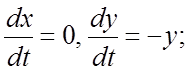 288.
288. 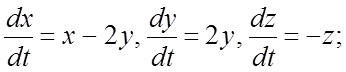
289. 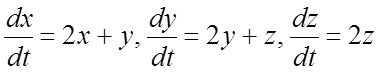 ; 290.
; 290. 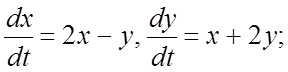
291. 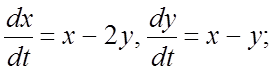 292.
292. 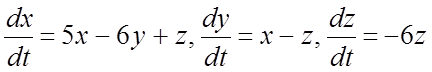 ;
;
293. 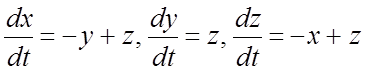 .
.
Найти общее решение методом Эйлера и, где указано, выделить решение, удовлетворяющее поставленным начальным условиям:
294. ![]()
295. ![]() 296.
296.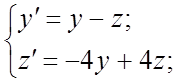
297.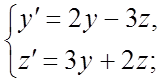 298.
298.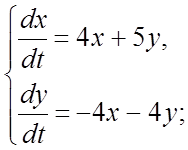 299.
299.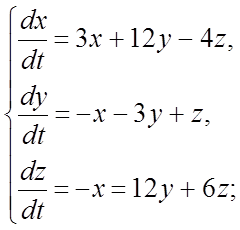
300.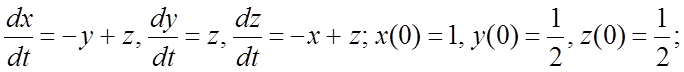
301.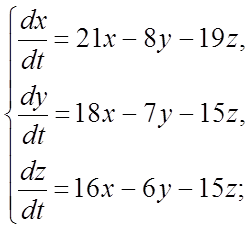 302.
302.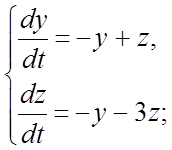 303.
303.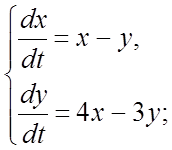
304.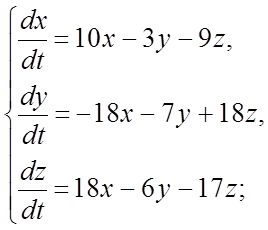 305.
305.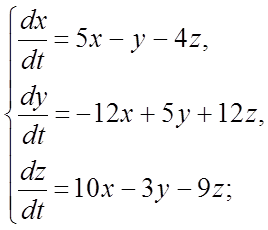
306.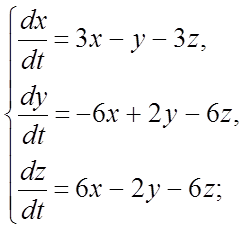 307.
307.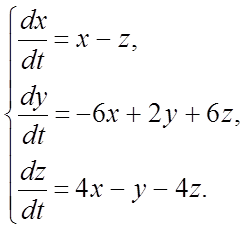
Найти общее решение методом вариации произвольных постоянных и, где указано, выделить решение, удовлетворяющее поставленным начальным условиям:
308.![]()
![]()
309.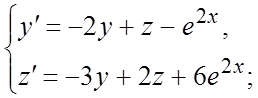 310.
310. 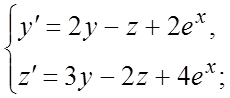
311. 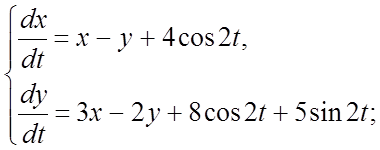
312. 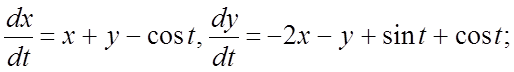
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.