39.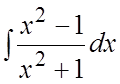 . 40.
. 40.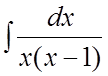 .
.
Найти интегралы методом замены переменной.
41.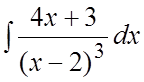 . 42.
. 42.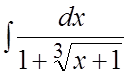 .
43.
.
43.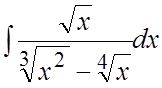 . 44.
. 44.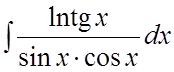 . 45.
. 45.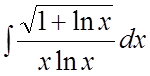 . 46.
. 46.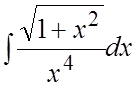 .
47.
.
47.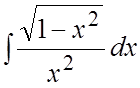 .
.
Найти интегралы методом интегрирования по частям.
48.![]() . 49.
. 49.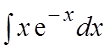 . 50.
. 50.![]() . 51.
. 51.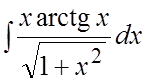 .
52.
.
52.![]() . 53.
. 53.![]() . 54.
. 54.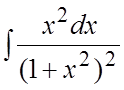 . 55.
. 55.![]() . 56.
. 56.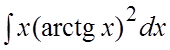 .
.
57.![]() . 58.
. 58.![]() . 59.
. 59.![]() . 60.
. 60.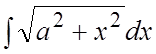
6.5 Интегрирование простейших функций, содержащих
квадратный трехчлен.
а) Интегралы вида
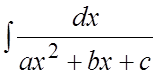 и
и 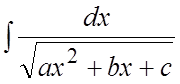 (5.1)
(5.1)
сводятся к табличным 13-16 после выделения из квадратного трехчлена полного квадрата.
Пример. Найти интеграл 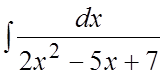 .
.
Ñ 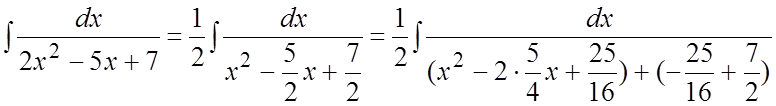 =
=
=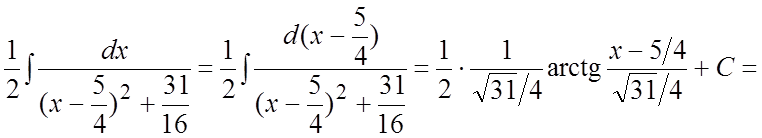
=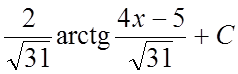 . #
. #
б) Интегралы
вида 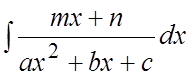 и
и 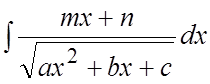 .
(5.2)
.
(5.2)
При
интегрировании таких функций сначала в числителе создаётся дифференциал
квадратного трехчлена: ![]() .
Числитель преобразуется следующим образом:
.
Числитель преобразуется следующим образом:
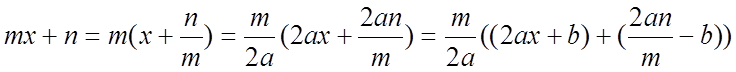 .
.
После этого
данный интеграл по свойству 5 раздела 6.2. разбивается на два: 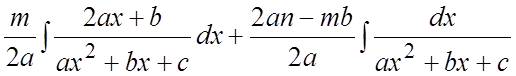 , первый из которых берётся по
, первый из которых берётся по
формуле 2 таблицы 6.3, а второй – интеграл (5.1), рассмотренный раньше. Аналогично берётся и второй интеграл из (5.2)
Пример. Найти интеграл 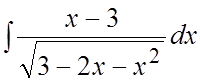 .
.
Ñ 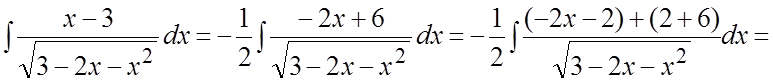
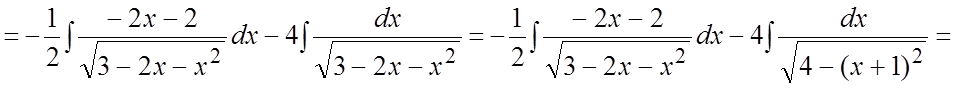
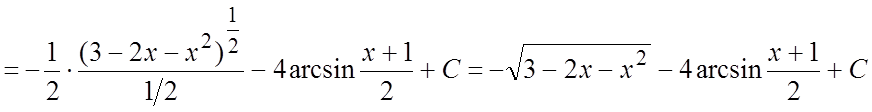 .#
.#
в) Интегралы
вида 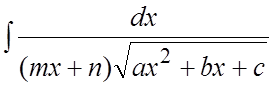 .
(5.3)
.
(5.3)
Эти интегралы
приводятся к интегралам (5.2) подстановкой 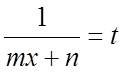 .
.
Пример. Найти интеграл 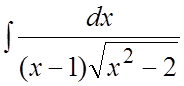 .
.
Ñ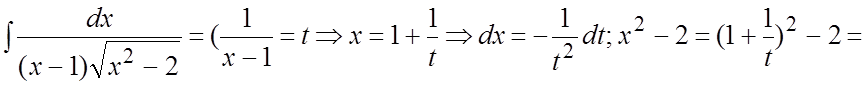
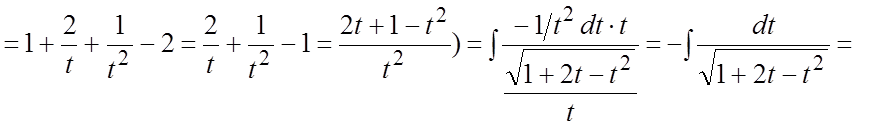
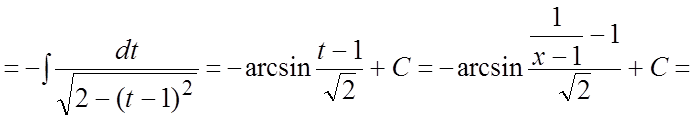
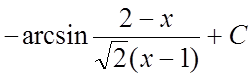 . #
. #
61.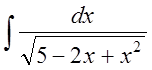 62.
62.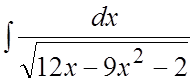 . 63.
. 63.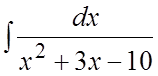 . 64.
. 64.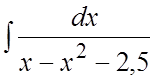 . 65.
. 65.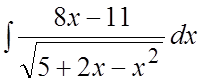 . 66.
. 66.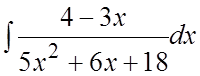 . 67.
. 67.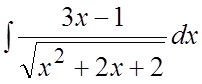 . 68.
. 68.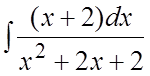 . 69.
. 69.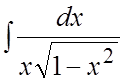 . 70.
. 70.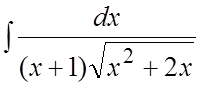 . 71.
. 71.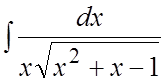 .
.
6.6. Рациональные дроби
Функция называется дробно-рациональной или рациональной дробью,
если она представляет собой дробь, в числителе и знаменателе которой стоят многочлены
степени m и n
соответственно, Для такой функции используют обозначение ![]() :
:
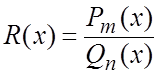 .
(6.1)
.
(6.1)
Если ![]() , дробь (6.1) называется правильной,
если же
, дробь (6.1) называется правильной,
если же ![]() - дробь (6.1) неправильная.
- дробь (6.1) неправильная.
Если дробь (6.1) неправильная, то в этой дроби можно выделить целую часть, т.е. представить её в виде:
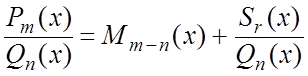 , (6.2)
, (6.2)
где ![]()
![]() и
и ![]() - многочлены, причем
- многочлены, причем ![]() , а значит дробь
, а значит дробь 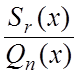 -
правильная Выделение целой части производится делением числителя
-
правильная Выделение целой части производится делением числителя ![]() на знаменатель
на знаменатель ![]() “уголком”.
“уголком”.
Пример. Выделить целую часть дроби 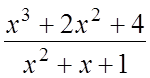 .
.
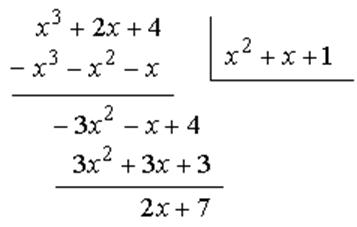
Целая часть
![]() . Итак,
. Итак, 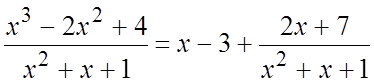 . #
. #
Дроби вида 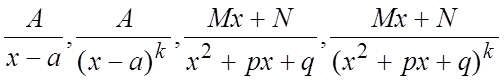 , (6.3)
, (6.3)
![]() ,
, ![]() , называются
простейшими или элементарными.
, называются
простейшими или элементарными.
Правильную рациональную дробь 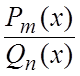 можно разложить на
сумму простейших дробей указанных четырёх типов (6.3). Это разложение зависит
от разложения на множители
можно разложить на
сумму простейших дробей указанных четырёх типов (6.3). Это разложение зависит
от разложения на множители ![]() .
.
Пусть![]() , (6.4)
, (6.4)
где ![]() соответствует действительному корню
соответствует действительному корню ![]()
![]() кратности
кратности ![]() , а
, а ![]() - паре
комплексных сопряженных корней
- паре
комплексных сопряженных корней ![]() кратности
кратности ![]() .
.
В разложении 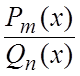 на элементарные дроби
сомножителю
на элементарные дроби
сомножителю ![]() из (6.4)
из (6.4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.