Глава 14
Кратные интегралы
14.1. Определение кратного интеграла
Определение двойного и тройного интеграла
Пусть : 1) в ограниченной
замкнутой области ![]() “ объема” v(E) задана ограниченная функция
“ объема” v(E) задана ограниченная функция ![]() ;
2)
;
2) ![]() - разбиение области
- разбиение области 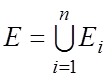 на
подобласти
на
подобласти ![]() с объемами
с объемами 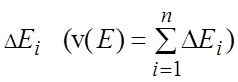 и диаметрами
и диаметрами
![]() ,
, ![]() -
диаметр разбиения; 3) зафиксируем точки
-
диаметр разбиения; 3) зафиксируем точки ![]() ,
, ![]() ; 4) построим интегральную сумму
; 4) построим интегральную сумму
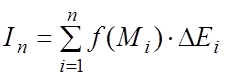 .
.
Определение. Конечный предел I интегральной суммы ![]() при
при ![]() называется
m- кратным интегралом от
функции f по области E и обозначается
называется
m- кратным интегралом от
функции f по области E и обозначается
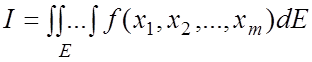
или 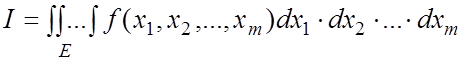 . (1.1)
. (1.1)
Таким образом, по определению,
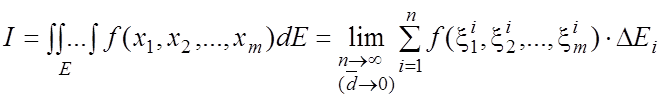 (1.2)
(1.2)
В этом случае функция ![]() называется интегрируемой в E.
называется интегрируемой в E.
При m=2 (m=3) для ограниченной функции f в замкнутой области ![]()
![]() )
кратный интеграл (1.1) называется двойным (тройным) интегралом,
а соответствующее определение (1.2) примет вид
)
кратный интеграл (1.1) называется двойным (тройным) интегралом,
а соответствующее определение (1.2) примет вид
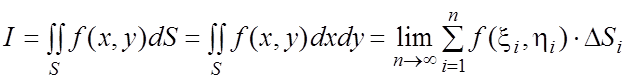 ,где
точка
,где
точка ![]() (
(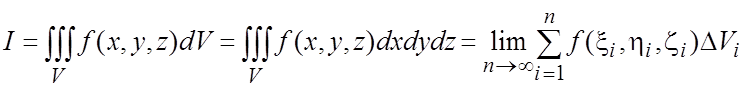 ,
,
где точка ![]() .
.
14.2. Двойные интегралы
14.2.1. Области на плоскости
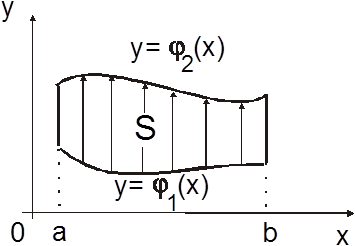
Определение. Область ![]() назовем
правильной в направлении Oy, если прямая, проходящая через любую внутреннюю точку из S параллельно оси Oy, пересекает границу области ровно в
двух точках (рис.14.1).
назовем
правильной в направлении Oy, если прямая, проходящая через любую внутреннюю точку из S параллельно оси Oy, пересекает границу области ровно в
двух точках (рис.14.1).
Область S будет правильной в направлении Oy , если существуют функции ![]() и
и ![]() ,
определенные и непрерывные на [a;b] и такие, что координаты точек,
принадлежащих (S),
удовлетворяют условиям:
,
определенные и непрерывные на [a;b] и такие, что координаты точек,
принадлежащих (S),
удовлетворяют условиям: ![]() ; тогда символически
можно записать:
; тогда символически
можно записать:
![]()
![]() . (2.1)
. (2.1)
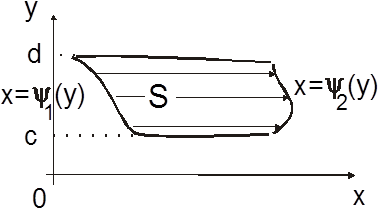
Область S
будет правильной в направлении Ox, если существуют функции ![]() и
и ![]() , определенные и непрерывные на [c;d] и такие, что координаты точек, принадлежащих S , удовлетворяют условиям:
, определенные и непрерывные на [c;d] и такие, что координаты точек, принадлежащих S , удовлетворяют условиям: ![]() (рис.14.2);
(рис.14.2);
тогда символически
![]() . (2.2)
. (2.2)
 |
 |
||
Область называется правильной, если она правильная в обоих направленияхOx иOy.
Пример 1. Область S задана уравнениями границы: ![]() .
.
Изобразить указанную область и записать как правильную.
|
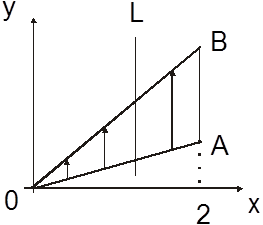 а) Область S – правильная в направлении Oy и любая прямая L, проходящая через внутреннюю точку
области, пересекает прямую
а) Область S – правильная в направлении Oy и любая прямая L, проходящая через внутреннюю точку
области, пересекает прямую 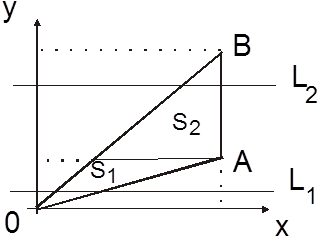
|
Пример 2. Точки из области D удовлетворяют неравенству ![]() (a>0) , т.е.
(a>0) , т.е. ![]() .
Изобразить данную область и записать как правильную.
.
Изобразить данную область и записать как правильную.
Ñ Преобразуя неравенство ![]() , получим
, получим ![]() . Геометрически
область D есть круг радиуса a/2 c центром в точке С(a/2; 0). Из уравнения границы
. Геометрически
область D есть круг радиуса a/2 c центром в точке С(a/2; 0). Из уравнения границы ![]() следует
следует
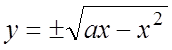 или
или 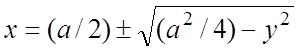 .Область
D может быть записана как правильная в
направлении Oy (любая
прямая, проходящая через внутреннюю точку D параллельно Oy, пересекает полуокружность
.Область
D может быть записана как правильная в
направлении Oy (любая
прямая, проходящая через внутреннюю точку D параллельно Oy, пересекает полуокружность 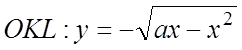 и
полуокружность OML:
и
полуокружность OML: 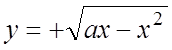 (рис. 14.5)), в силу (2.1)
(рис. 14.5)), в силу (2.1) 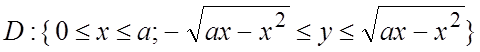 .
.
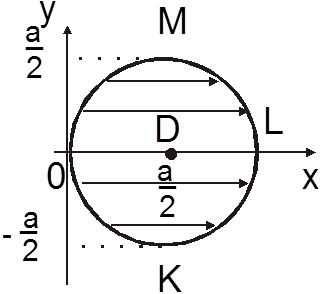 |
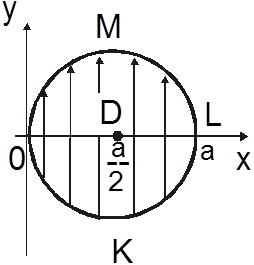 Рис.
14.5 Рис.14.6
Рис.
14.5 Рис.14.6
Область D можно записать как правильную в направлении Ox (прямая, проходящая через внутреннюю точку D параллельно Ox пересекает полуокружность
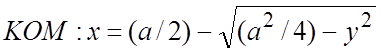 и полуокружность
и полуокружность ![]() +
+ 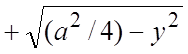 (рис. 14.6)), и в силу (2.2):
(рис. 14.6)), и в силу (2.2): ![]()
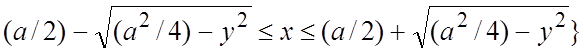 #
#
Задачи для самостоятельного решения
Изобразить указанные области и записать как правильные в направлении Oy.
1. S – параллелограмм со сторонами x=3, x=5, 3x-2y+4=0, 3x-2y+1=0.
2.
Область D задана неравенствами ![]() .
.
3.
Область D – треугольник со сторонами ![]() .
.
14.2.2. Повторный интеграл
Определение. Повторный интеграл 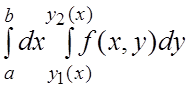 есть приращение первообразной F(x,y)
для
есть приращение первообразной F(x,y)
для![]() по переменному “y”, проинтегрированное по переменному
“x” , т.е.
по переменному “y”, проинтегрированное по переменному
“x” , т.е.
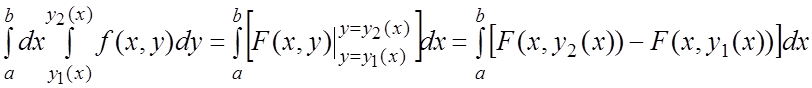 .
.
Определение. Повторный интеграл 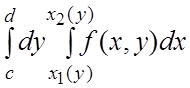 есть приращение первообразной Ф(x,y) для f(x,y) по переменному “x”, проинтегрированное по переменному “y”, т.е.
есть приращение первообразной Ф(x,y) для f(x,y) по переменному “x”, проинтегрированное по переменному “y”, т.е.
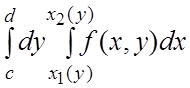 =
=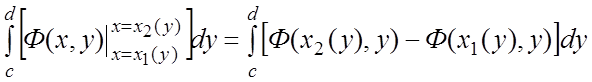 .
.
Пример 3. Вычислить повторный интеграл 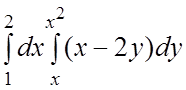 .
.
Ñ 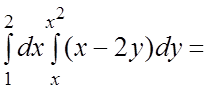 ½интегрируя внутренний интеграл по “y”, полагаем “x” постоянным½=
½интегрируя внутренний интеграл по “y”, полагаем “x” постоянным½=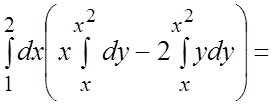
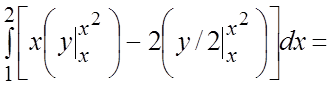
= 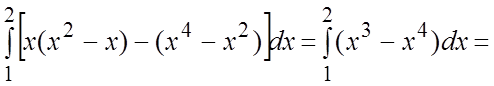
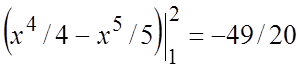 . #
. #
Задачи для самостоятельного решения
Вычислить повторные интегралы.
4. 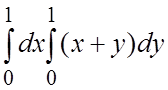 . 5.
. 5. 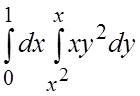 6.
6.
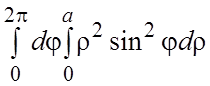 . 7.
. 7. 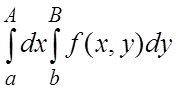 , если
, если ![]() .
.
14.2.3. Вычисление двойного интеграла в декартовых
координатах
Теорема 14.1 Если : 1) функция f(x,y)
интегрируема в правильной в направлении Oy области S: ![]() , т.е. существует двойной интеграл
, т.е. существует двойной интеграл 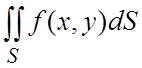 , 2) существует повторный интеграл
, 2) существует повторный интеграл 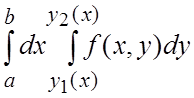 , то
, то
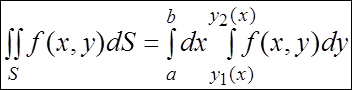 (2.3)
(2.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.