Задачи для самостоятельного решения
Проверить, являются ли следующие функции оригиналами; в
случае положительного ответа найти их показатели роста (множитель ![]() опущен):
опущен):
1. ![]() ,
, ![]() ; 2.
; 2.
![]() . 3.
. 3. 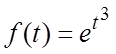 4.
4. 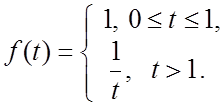
5. ![]() . 6.
. 6. 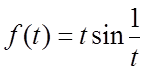 . 7.
. 7. ![]() .
.
Пользуясь определением (1.3), найти изображения следующих функций:
8. ![]() ; 9.
; 9.![]() ; 10.
; 10.![]() ; 11.
; 11. 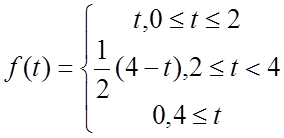 12.
12.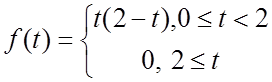
Используя свойства I-IX и таблицу изображений «основных» функций, найти изображения нижеследующих функций:
13. ![]() ; 14.
; 14. 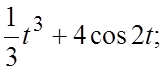 15.
15.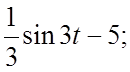 16.
16. ![]() 17.
17.![]() 18.
18. ![]() 19.
19. ![]() 20.
20.![]() 21.
21.![]()
22. 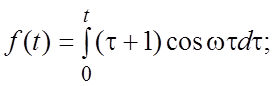 23.
23. 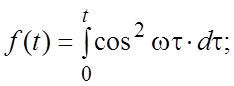 24.
24.![]()
25. 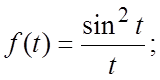 26.
26.  27.
27. 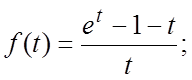 28.
28. ![]()
29. ![]()
В задачах 30-32 построить график функции: с помощью единичной функции Хевисайда записать ее одним аналитическим выражением и найти ее изображение:
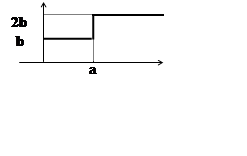
30. 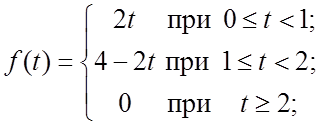 31.
31. 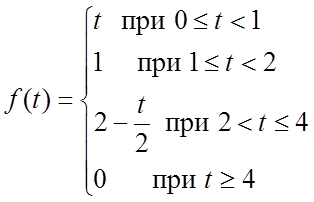
32. 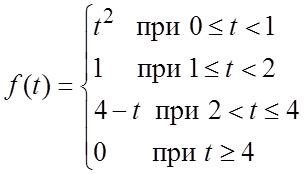
В задачах 33-35 построить график функции ![]() и найти ее изображение:
и найти ее изображение:
33. ![]() 34.
34. ![]()
35. ![]()
В задачах 36-39 найти изображения функций, заданных графически:
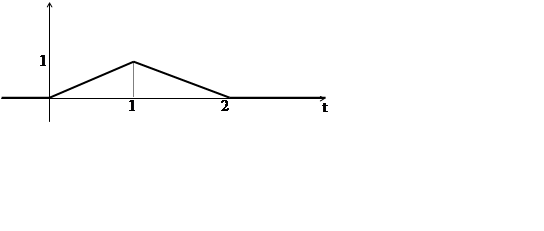 36. 37.
36. 37.
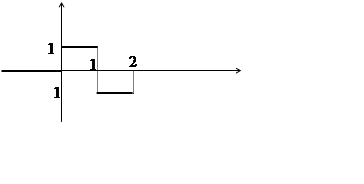
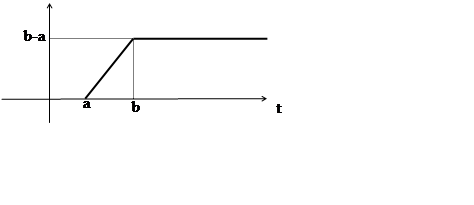
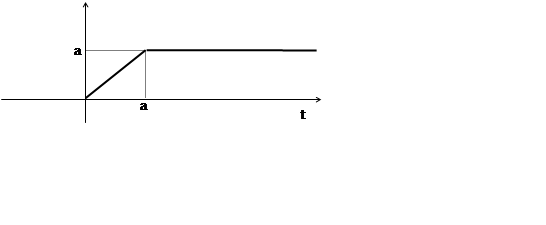
![]() 38.
39.
38.
39.
В задачах 40-42 найти изображения функций, используя свойства (1.6) и (1.11) – совместную теорему подобия и запаздывания:
40. 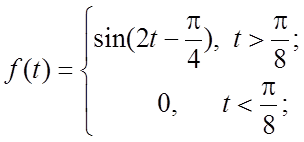 41.
41. 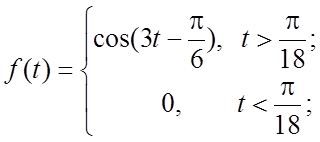
42. 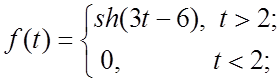
Найти изображение следующих функций:
43. 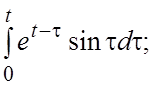 44.
44. 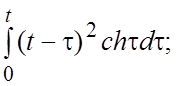 45.
45. 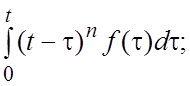 46.
46. 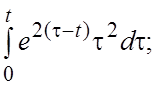
В нижеследующих задачах восстановить оригинал по изображению, используя элементарные методы:
47. 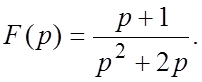 48.
48. 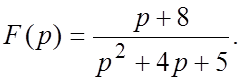 49.
49. 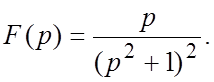
50. 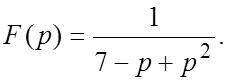 51.
51.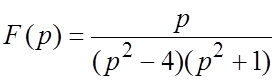 ;
52.
;
52. 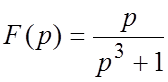
53. 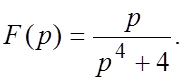 54.
54. 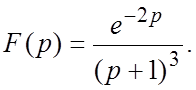 55.
55. 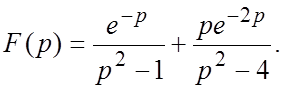
56. 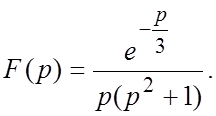 57.
57. 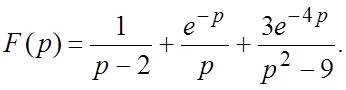
58. 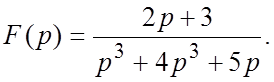 59.
59. 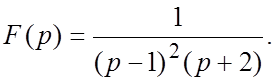
60. 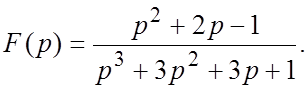 61.
61. 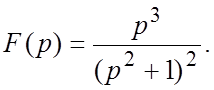
62. 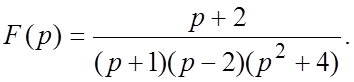 63.
63. 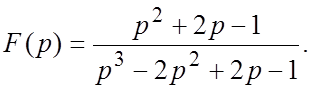
64. 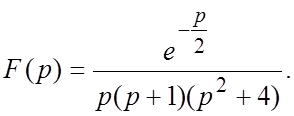
Пользуясь первой теоремой разложения, найти оригиналы для заданных изображений:
65. 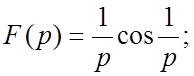 66.
66. 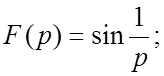 67.
67. 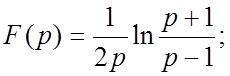
68. 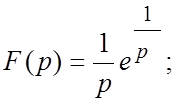 69.
69. 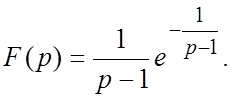
Пользуясь второй теоремой разложения или с помощью разложения на простейшие дроби, найти оригиналы заданных изображений:
70. 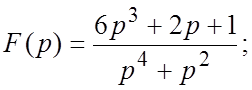 71.
71. 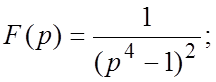 72.
72. 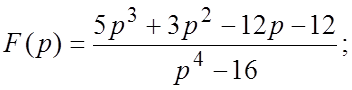
73. 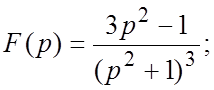 74.
74. 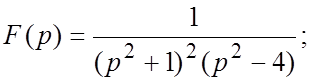 75.
75. 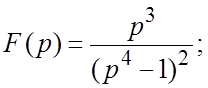
76. 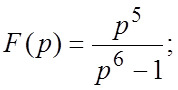 77.
77. 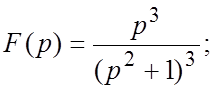 78.
78. 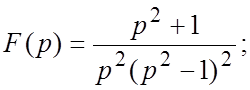
79. 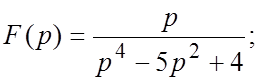 80.
80. 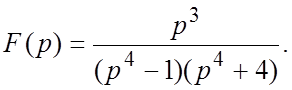
Найти общие решения дифференциальных уравнений:
81. ![]() 82.
82. ![]() 83.
83. ![]()
84. ![]()
Решить задачу Коши для заданных дифференциальных уравнений:
85. ![]()
![]() ,
, ![]() 86.
86.![]()
![]()
![]()
87. ![]()
![]()
![]() 88.
88. ![]()
![]()
![]()
89. ![]()
![]()
![]() 90.
90. ![]()
![]()
91. ![]()
![]() 92.
92. ![]()
![]() 93.
93. ![]()
![]()
![]()
Найти решения нижеследующих дифференциальных уравнений при нулевых начальных условиях:
94. ![]() где
где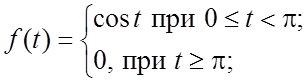
95. ![]() где
где 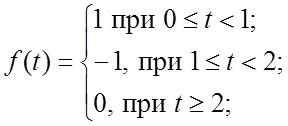
96. ![]() 97.
97.
![]()
 |
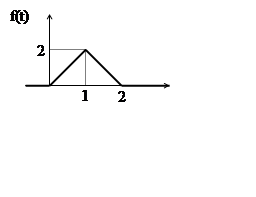
![]()
![]()
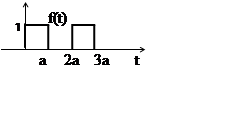 |
![]() 98.
98. ![]()
Найти общее или частное решения общих линейных однородных уравнений с переменными коэффициентами:
99. ![]() 100.
100. ![]()
101. ![]()
![]()
![]()
102. ![]()
![]()
![]()
Решить следующие уравнения с запаздывающим аргументом при нулевых начальных условиях:
103. ![]() 104.
104. ![]() 105.
105. ![]()
106. ![]()
С помощью формулы Дюамеля (2.9) решить уравнения при нулевых начальных условиях:
107. 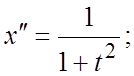 108.
108. ![]() 109.
109. ![]() 110.
110. 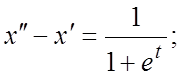
111. ![]() а)
а) 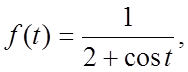 б)
б) 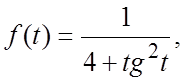 в)
в) 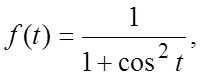
г) 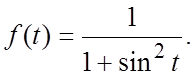 112.
112. ![]() 113.
113. 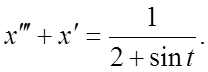
Решить системы уравнений:
114. 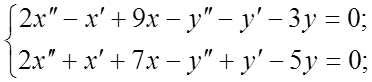 115.
115. 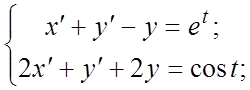
![]()
116. 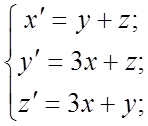
![]()
![]()
![]() .
.
117. 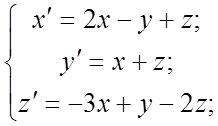
![]()
![]()
![]()
118. 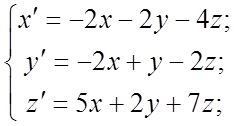
![]()
119. 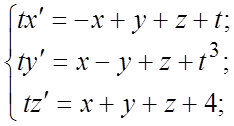
![]()
120. 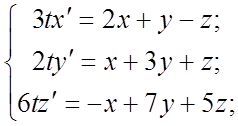
![]()
Ответы к задачам главы 17
1.
Да; ![]() . 2. Да; S0=3. 3. Нет. 4. Да; S0=0,5. 5. Да; S0=0,6. 6. Да; S0=0,7.
. 2. Да; S0=3. 3. Нет. 4. Да; S0=0,5. 5. Да; S0=0,6. 6. Да; S0=0,7.
7.
Нет. 8. ![]() . 9.
. 9. 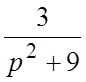 . 10.
. 10.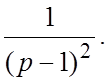 11.
11. 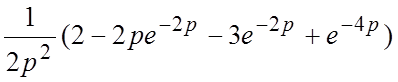
12.
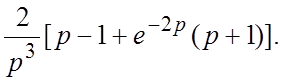 13.
13. 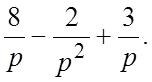 14.
14. 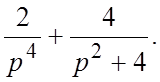 15.
15. 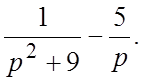
16. 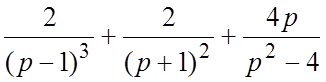 17.
17. 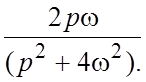 18.
18. 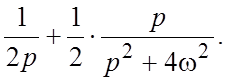
19. 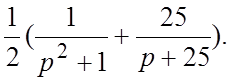 20.
20. 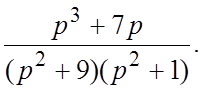 21.
21. 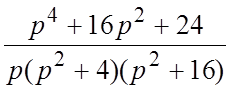
22. 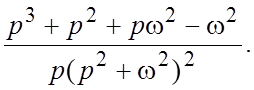 23.
23. 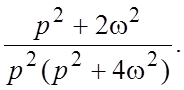 24.
24. 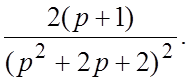
25. 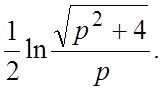 26.
26. 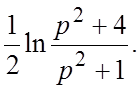 27.
27. 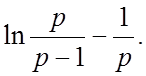 28.
28. 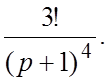
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.