Задачи для самостоятельного решения
Найти потенциалы следующих плоских и трехмерных полей:
91. ![]() ; 92.
; 92. 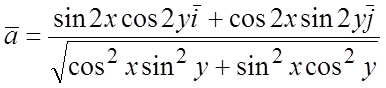 ;
;
93. ![]() ; 94.
; 94. ![]() ;
;
95. ![]() ; 96.
; 96. 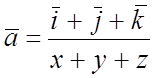 ; 97.
; 97. 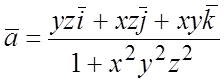 ;
;
98. 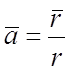 ; 99.
; 99. 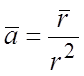 ; 100.
; 100. ![]() ;
;
101. 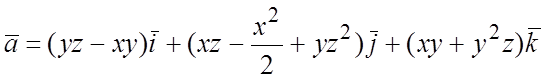 ;
;
102. 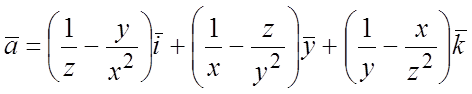 ;
;
103.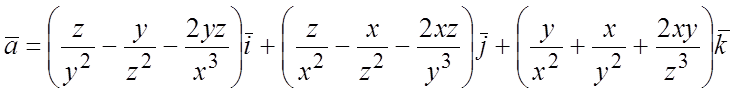 .
.
104. Доказать, что поле вихрей
соленоидально: ![]() .
.
105. Доказать, что в соленоидальном поле поток вектора через замкнутую поверхность, не содержащую внутри особых точек, равен нулю.
В задачах 106 – 109 проверить соленоидальность заданных полей:
106. ![]() ; 107.
; 107.
![]() ;
;
108. 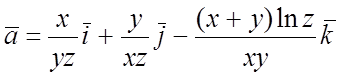 ; 109.
; 109. 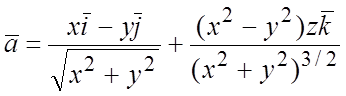 .
.
110. Доказать, что в соленоидальном поле поток вектора поля через поперечное сечение любой векторной трубки (определенный в одном и том же направлении) сохраняет постоянное значение.
111. Показать, что поле вектора 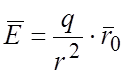 соленоидально во всякой области, не
содержащей начало координат O(0,0,0).
соленоидально во всякой области, не
содержащей начало координат O(0,0,0).
112. Найти условие соленоидальности поля ![]() .
.
113. Показать, что в соленоидальном поле
поток вектора ![]() не зависит от вида поверхности (S), натянутой на данный контур (L), а зависит только от самого контура.
не зависит от вида поверхности (S), натянутой на данный контур (L), а зависит только от самого контура.
114.Показать, что векторное поле ![]() - соленоидальное и безвихревое.
- соленоидальное и безвихревое.
Используя правило
применения оператора ![]() к произведениям скалярных и векторных
полей, доказать справедливость следующих формул:
к произведениям скалярных и векторных
полей, доказать справедливость следующих формул:
115. ![]() ; 116.
; 116.
![]() ;
;
117.![]() ; 118.
; 118.![]() ;
;
119. ![]() ;
;
120. ![]() ;
;
121. ![]() .
.
122. Найти ![]() . В
каком случае
. В
каком случае ![]() ?
?
123. Показать, что скалярное поле 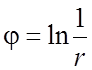 ,
, 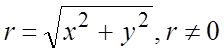 ,
является гармоническим
,
является гармоническим 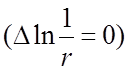 .
.
В задачах 124 – 131 выяснить, какие поля – гармонические, какие – нет:
124. 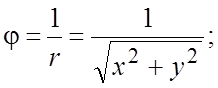 125.
125. 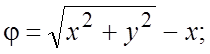 126.
126. ![]()
127. ![]() 128.
128. ![]()
129.![]()
130. ![]()
131. ![]()
![]()
132. Найти все гармонические поля, зависящие только от x.
133. Найти общий вид однородного гармонического многочлена второй степени от x и y.
134. Найти все решения уравнения Пуассона
![]() , зависящие только от x.
, зависящие только от x.
Ответы к задачам главы 15
1. ![]() 2.
2.![]() 3.
3. ![]() 4.
4.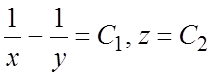 . 5.
. 5.![]() 6.
6. 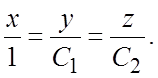
7.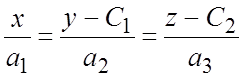 . 8.
. 8. ![]() 9.
9.
![]()
10. ![]() 11.
11. ![]()
12. ![]() 13.
13. 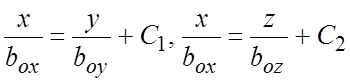 .
14.
.
14. 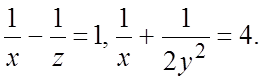
15. ![]() 16.
16. ![]() 17.
17.
![]() 18.
18. ![]() 19.
19. 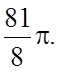 20.0. 21.
20.0. 21. ![]() 22. 0,25.
23.
22. 0,25.
23. ![]() 24.
24. ![]() 25.
25. ![]() 26.
26. ![]() 27.
27. ![]() 28.
28. ![]()
29. ![]() 30.
30. ![]() 31.
31.
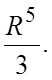 32.
32. ![]() 33.
33. 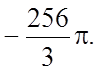 34.
34. ![]() 35.0.
35.0.
36. ![]() 37. а) 2/3; б) 0,7; в) 0,7;
г)1; д) 1. 38.
37. а) 2/3; б) 0,7; в) 0,7;
г)1; д) 1. 38. 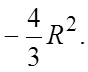 39.
39. ![]() 40.
40.
![]()
41. ![]() 42.
42. ![]() 43.
43.
![]() 44.
44. ![]() 45.
45. ![]() 46. –14. 47.
46. –14. 47. ![]() 48.
48.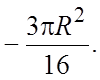 49.
49. ![]() 50.
50. 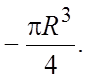 51. 4/3. 52.
51. 4/3. 52. ![]() 53.
53. ![]() . 54.
. 54. 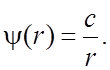
55. ![]() 56. 0. 57. 0.
58.
56. 0. 57. 0.
58. 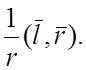 59. 0. 60. 1. 61.
59. 0. 60. 1. 61. ![]() 62.
62. ![]() 63.
63. 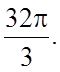
64. 0. 65. ![]() 66.
66.
![]() 67.
67.![]() 68.
68. ![]() 69.
69. ![]() 70.
70. ![]() 71.-1. 72.
71.-1. 72.![]() 73.
73. ![]() 74.
74. ![]() 81.
81. ![]()
![]() 82.
82. ![]() 83.
83.![]() 84.
84. ![]() 85.
85.![]() 86.
86. ![]() 87.
87. ![]() 88. 0.
88. 0.
89. ![]() 90.
90.![]() 91.
91. ![]() 92.
92. 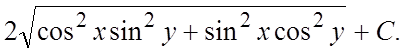 93.
93. ![]() 94.
94.![]() 95.
95. ![]() 96.
96. ![]() 97.
97. ![]() 98. r. 99. lnr. 100.
98. r. 99. lnr. 100. 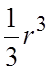 . 101.
. 101. 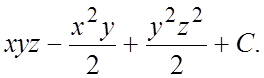 102.
102. 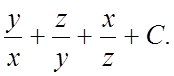
103. 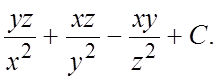 112.
112. ![]()
![]() C=const. 122.
C=const. 122.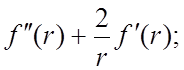
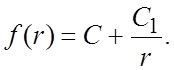 124.
Нет. 125. Нет. 126. Да. 127.
Только при A+C=0.
124.
Нет. 125. Нет. 126. Да. 127.
Только при A+C=0.
128. Только, если A+C=B+D=0.
129. Да. 130. Только при ![]()
131. Только если ![]()
![]() .
.
132. ![]() 133.
133. ![]() A и B – любые.
A и B – любые.
134. 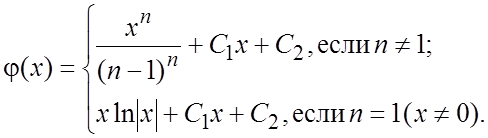
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.