Теорема 14.2. Если :1) функция f(x,y)
интегрируема в правильной в направлении Ox области ![]() , т.е. существует
двойной интеграл
, т.е. существует
двойной интеграл 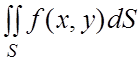 , 2) существует повторный
интеграл
, 2) существует повторный
интеграл 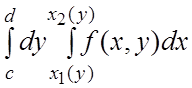 , то
, то
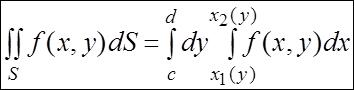 . (2.4)
. (2.4)
Из вышеприведенных теорем следует, что при вычислении повторного интеграла можно изменять порядок интегрирования.
Пример 4. Изменить порядок интегрирования в
интеграле 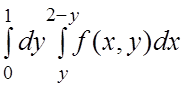 .
.
|
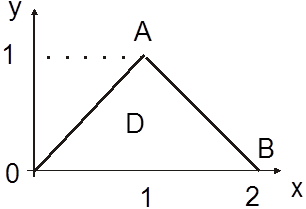 Ñ Так как из (2.4) имеем
Ñ Так как из (2.4) имеем 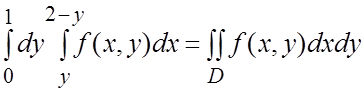 , то правильная в направлении Ox область D ограничена линиями x=y, x=2-y, y=0, y=1
(линия y =1 выродилась в точку) (рис. 14.7).
Эта область является правильной и в направлении Oy. Так как участок OABграницы состоит из отрезков прямых
, то правильная в направлении Ox область D ограничена линиями x=y, x=2-y, y=0, y=1
(линия y =1 выродилась в точку) (рис. 14.7).
Эта область является правильной и в направлении Oy. Так как участок OABграницы состоит из отрезков прямых ![]() . Итак,
. Итак, 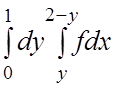 =
=
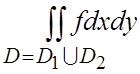 =
= 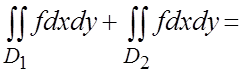 =
=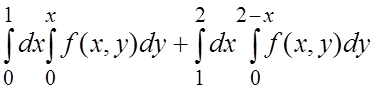 .#
.#
Пример 5. Вычислить 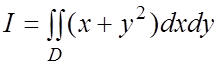 по
области D, ограниченной линиями
по
области D, ограниченной линиями ![]() и
и ![]() .
.
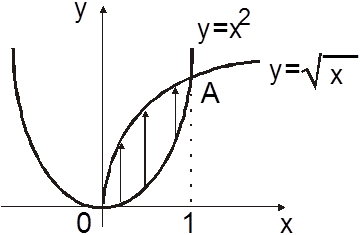 Ñ Изобразим область D. Для отыскания точек пересечения
парабол
Ñ Изобразим область D. Для отыскания точек пересечения
парабол ![]() и
и ![]() решаем
уравнение
решаем
уравнение ![]()
![]() , откуда имеем действительные
корни
, откуда имеем действительные
корни ![]() ,
, ![]() . Таким
образом, параболы пересекаются в точках
. Таким
образом, параболы пересекаются в точках ![]() ( рис.
14.8). Рассматривая D
как правильную в направлении Oy
(рис.14.8а), имеем (см.(2.1))
( рис.
14.8). Рассматривая D
как правильную в направлении Oy
(рис.14.8а), имеем (см.(2.1)) ![]() . По формуле (2.3)
. По формуле (2.3)
Рис.14.8 а) 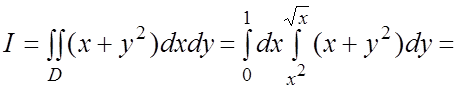
=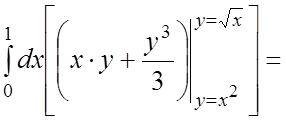
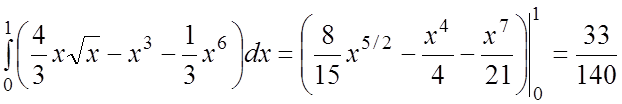 .
.
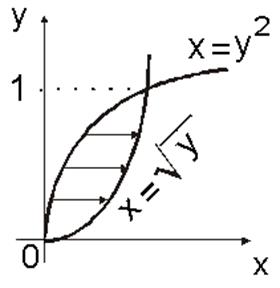 Если область D рассматривать как правильную в направлении Ox (рис.14.8б), то (см. (2.2))
Если область D рассматривать как правильную в направлении Ox (рис.14.8б), то (см. (2.2)) ![]() . По формуле (2.4)
. По формуле (2.4)
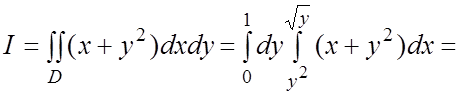
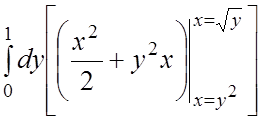 =
=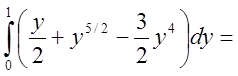
|
=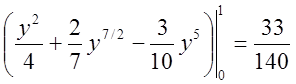 . #
. #
Задачи для самостоятельного решения
Изменить порядок интегрирования в следующих повторных интегралах:
8. 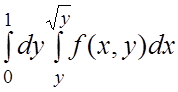 . 9.
. 9. 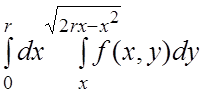 .
.
10. 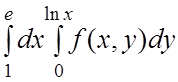 . 11.
. 11. .
.
Перейти от двойного интеграла 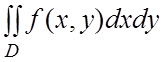 по
конечной области D к повторному
интегралу и расставить пределы интегрирования:
по
конечной области D к повторному
интегралу и расставить пределы интегрирования:
12.
Область D – параллелограмм со сторонами ![]()
![]()
![]() .
.
13.
![]() . 14.
. 14. ![]() .
.
15.
![]() - треугольник со сторонами
- треугольник со сторонами ![]() .
.
16.
![]() .
.
17.
![]() - треугольник с вершинами
- треугольник с вершинами ![]() .
.
18.
D – сегмент, ограниченный линиями ![]() .
.
Вычислить двойные интегралы:
19. 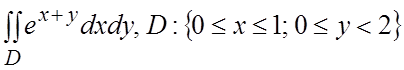 . 20.
. 20. 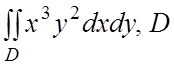 - круг
- круг ![]() .
.
21.
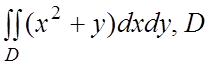 - область, ограниченная линиями
- область, ограниченная линиями ![]() .
.
22.
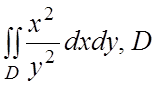 - область, ограниченная линиями
- область, ограниченная линиями ![]() .
.
23. 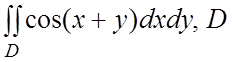 - область, ограниченная
линиями
- область, ограниченная
линиями ![]() .
.
24.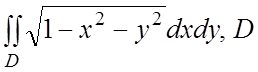 - четверть круга
- четверть круга ![]() , лежащая в первом квадранте.
, лежащая в первом квадранте.
25. 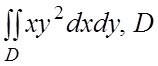 - область, ограниченная
параболой
- область, ограниченная
параболой ![]() и прямой
и прямой ![]() .
.
26. 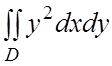 , если D ограничена осью абсцисс и первой
аркой циклоиды
, если D ограничена осью абсцисс и первой
аркой циклоиды ![]() ,
, ![]() ,
, ![]() .
.
14.2.4. Замена переменных в двойном интеграле.
Пусть функции ![]() осуществляют взаимно однозначное
непрерывно дифференцируемое отображение области P плоскости
осуществляют взаимно однозначное
непрерывно дифференцируемое отображение области P плоскости ![]() на область S плоскости
на область S плоскости ![]() .
Тогда существует обратное непрерывно дифференцируемое отображение
.
Тогда существует обратное непрерывно дифференцируемое отображение ![]() ,
, ![]() области
S на область P, если якобиан преобразования
области
S на область P, если якобиан преобразования
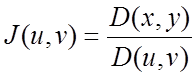 =
=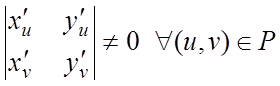 .
.
Величины u и v можно рассматривать как прямоугольные координаты для точек области P и в то же время как криволинейные координаты точек области S. Точки плоскости Oxy, для которых одна из координат u и v сохраняет постоянное значение, образуют координатную линию. Всего будет два семейства таких линий.
Теорема 14.3. Пусть ![]() есть
дифференцируемое преобразование области P из плоскости
есть
дифференцируемое преобразование области P из плоскости ![]() на
область Sиз плоскости
на
область Sиз плоскости ![]() .
Тогда справедливо равенство
.
Тогда справедливо равенство
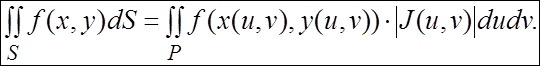 (2.5)
(2.5)
Замечание. Равенство (2.5) сохраняет справедливость, когда условие взаимно однозначного соответствия между областями S и P нарушается в отдельных точках или вдоль отдельных линий.
Переход в двойном интеграле к полярным координатам
Формулы
![]() (2.6)
(2.6)
преобразуют полярные координаты ![]() точки в декартовы координаты этой точки и
переводят область
точки в декартовы координаты этой точки и
переводят область ![]() (или область
(или область ![]() ) на всю плоскость Oxy.
) на всю плоскость Oxy.
Обратное преобразование
декартовых координат в полярные осуществляется по формулам: 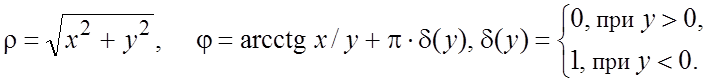
Фиксируя в последних формулах ![]() и
и![]() , получим координатные
линии из разных семейств: окружность с центром в точке
, получим координатные
линии из разных семейств: окружность с центром в точке ![]() и
луч, исходящий из точки
и
луч, исходящий из точки ![]() .
.
Якобиан преобразования
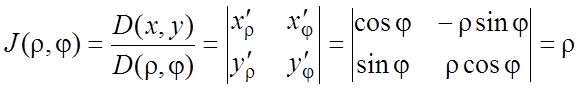
и формула (2.5) принимает вид:
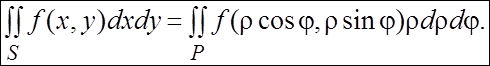 (2.7)
(2.7)
Рекомендация. К полярным координатам
целесообразно переходить, когда в подынтегральное выражение или в уравнения
границы области интегрирования входит комбинация ![]() .
.
В некоторых случаях при
вычислении двойного интеграла удобно перейти от декартовых координат к эллиптическим
полярным координатам ![]()
![]()
![]() по формулам
по формулам
![]() ,
, ![]() (2.8)
(2.8)
![]() - постоянные,
- постоянные, ![]() .
Тогда
.
Тогда
![]() ,
, ![]() (2.9)
(2.9)
Пример 6. Записать в полярной системе
координат область S
, заданную в декартовой системе координат неравенством ![]() (круг
радиуса R с центром в точке
(круг
радиуса R с центром в точке ![]() ).
).
Ñ Перейдем от декартовых координат x, y к полярным ![]() по
формулам
по
формулам ![]() ,
, ![]() . Подставим x и y в исходное неравенство, получим:
. Подставим x и y в исходное неравенство, получим: ![]() или
или ![]() . На
координату j дополнительных
ограничений не накладывается, поэтому
. На
координату j дополнительных
ограничений не накладывается, поэтому ![]() (или
(или ![]() ).
).
В полярной системе
координат круг записывается неравенствами: ![]() . #
. #
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.