точки,
определяемое этим уравнением. Задача Коши заключается в определении движения,
удовлетворяющего начальным условиям: 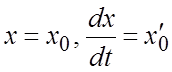 при
при ![]() , где числа
, где числа ![]() и
и ![]() (начальные данные) есть соответственно
начальный момент времени, начальная координата и проекция скорости в
(начальный) момент времени
(начальные данные) есть соответственно
начальный момент времени, начальная координата и проекция скорости в
(начальный) момент времени ![]() .
.
Пример 1. Показать, что ![]() есть общее решение
дифференциального уравнения
есть общее решение
дифференциального уравнения ![]() .
.
Решение. 1. Покажем, что ![]() удовлетворяет
данному уравнению при любых
удовлетворяет
данному уравнению при любых ![]() . Имеем
. Имеем ![]() . 2. Пусть заданы произвольные начальные
условия
. 2. Пусть заданы произвольные начальные
условия ![]() ,
, ![]() .
Покажем, что постоянные
.
Покажем, что постоянные ![]() можно подобрать так,
что эти начальные условия будут удовлетворены. Составим систему:
можно подобрать так,
что эти начальные условия будут удовлетворены. Составим систему: ![]() из которой однозначно определяются
из которой однозначно определяются ![]() . Таким образом, решение
. Таким образом, решение ![]() удовлетворяет поставленным начальным
условиям. Заметим, что запись
удовлетворяет поставленным начальным
условиям. Заметим, что запись ![]() означает, что решение
задачи записано в форме Коши.
означает, что решение
задачи записано в форме Коши.
Пример 2. Найти область существования и единственности решения уравнения
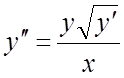 .
.
Решение. Функция 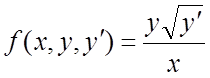 и ее частная
производная
и ее частная
производная 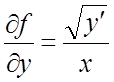 непрерывны при
непрерывны при ![]() , то есть данное уравнение имеет
единственное решение при
, то есть данное уравнение имеет
единственное решение при ![]() .
.
10.5.2. Интегрируемость в квадратурах
Уравнение n-го порядка во многих случаях удается проинтегрировать в квадратурах путем предварительного сведения его к уравнению более низкого порядка или при помощи нахождения промежуточных интегралов
![]() (5.7)
(5.7)
- соотношений, получаемых в результате интегрирования исходного уравнения (такое соотношение называется промежуточным интегралом k-го порядка дифференциального уравнения (1.2)). Ниже рассматриваются дифференциальные уравнения, допускающие понижение порядка не только в форме (1.2), но и в общем виде (1.1).
1) Уравнения вида
![]()
Общее решение уравнения вида
![]() (5.8)
(5.8)
получается путем n – кратного интегрирования:
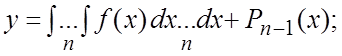
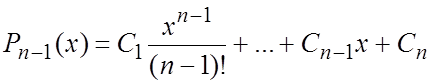 ,
(5.9)
,
(5.9)
или по формуле
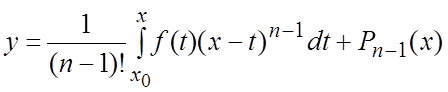 (5.9¢)
(5.9¢)
Пример 1. Найти общее решение уравнения 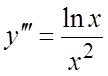 и
выделить решение, удовлетворяющее начальным условиям:
и
выделить решение, удовлетворяющее начальным условиям: ![]() .
.
Решение. Интегрируем это уравнение последовательно три раза: 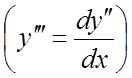
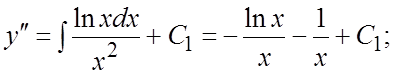
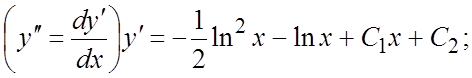
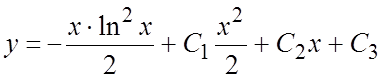 . Найдем решение, удовлетворяющее заданным
начальным условиям. Подставляя начальные данные в
. Найдем решение, удовлетворяющее заданным
начальным условиям. Подставляя начальные данные в ![]() ,
получим систему для определения произвольных постоянных:
,
получим систему для определения произвольных постоянных: 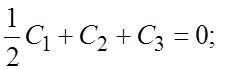
![]()
![]() , откуда
, откуда ![]()
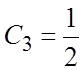 . Искомое решение
. Искомое решение 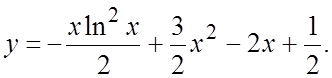
2) Уравнение, не содержащее искомой функции и
последовательных k-1 первых производных
Уравнение вида
![]()
![]() (5.10)
(5.10)
подстановкой![]() приводится к уравнению (n-k)-го порядка
приводится к уравнению (n-k)-го порядка ![]() . Если удается получить общее решение
последнего уравнения в виде
. Если удается получить общее решение
последнего уравнения в виде ![]() (получить
промежуточный интеграл k-го порядка исходного
уравнения (5.10)), то задача нахождения решения сводится к задаче (5.8),
решение которой дано в п.10.5.2 .
(получить
промежуточный интеграл k-го порядка исходного
уравнения (5.10)), то задача нахождения решения сводится к задаче (5.8),
решение которой дано в п.10.5.2 .
Пример 2. Найти частное решение уравнения ![]() ,
удовлетворяющее начальным условиям:
,
удовлетворяющее начальным условиям: 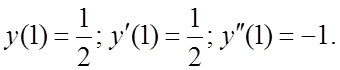
Решение. Уравнение не содержит y и ![]() . Положим
. Положим ![]() ;
уравнение принимает вид
;
уравнение принимает вид ![]() или
или 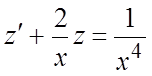 . Это линейное уравнение первого порядка.
Его общее решение
. Это линейное уравнение первого порядка.
Его общее решение 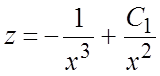 . Используя начальное условие
. Используя начальное условие ![]() , находим
, находим ![]() и,
следовательно,
и,
следовательно, 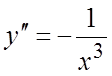 , откуда
, откуда 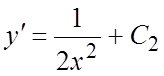 .
Начальное условие
.
Начальное условие 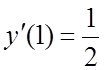 позволяет определить
позволяет определить ![]() . Интегрируя еще раз, получаем
. Интегрируя еще раз, получаем 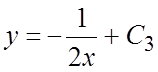 , и из условия
, и из условия ![]() следует,
что
следует,
что ![]() . Искомое частное решение
. Искомое частное решение 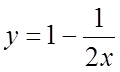 .
.
Пример 3. Найти решения уравнения ![]() ,
удовлетворяющие начальным условиям: а)
,
удовлетворяющие начальным условиям: а) ![]() при x = 0; б)
при x = 0; б) ![]() при x = 0.
при x = 0.
Решение. Интегрируем уравнение: ![]() ,
, 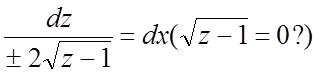 ,
, ![]() ,
, ![]() ,
, ![]() ,
, 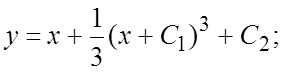
![]()
![]() . Следовательно, уравнение имеет общее
решение
. Следовательно, уравнение имеет общее
решение 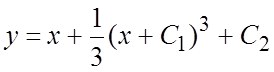 и семейство особых решений
и семейство особых решений ![]() .
.
Найдем
решения поставленных задач Коши: а) воспользуемся общим решением. Имеем 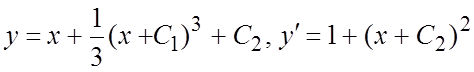 (*). Полагая здесь
(*). Полагая здесь ![]() ,
получаем систему уравнений для определения произвольных постоянных:
,
получаем систему уравнений для определения произвольных постоянных: 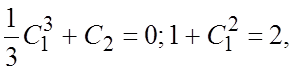 откуда
откуда ![]() Подставляя
эти значения
Подставляя
эти значения ![]() и
и ![]() в (*),
найдем два решения:
в (*),
найдем два решения: 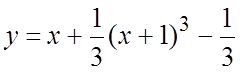 и
и 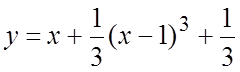 .
Других решений нет, так как ни одно из особых решений не удовлетворяет
рассматриваемым начальным условиям; б) подставляя в систему (*) начальные
данные
.
Других решений нет, так как ни одно из особых решений не удовлетворяет
рассматриваемым начальным условиям; б) подставляя в систему (*) начальные
данные ![]() , получаем:
, получаем: 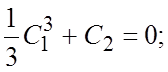
![]() , откуда
, откуда ![]() и
и 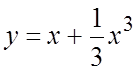 . Из особых решений y
= x удовлетворяет рассматриваемым начальным
данным.
. Из особых решений y
= x удовлетворяет рассматриваемым начальным
данным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.