Глава 5. Исследование функций с помощью производных
5.1. Возрастание и убывание функций.
Функция f (x)
называется возрастающей (неубывающей) на интервале (a,b), если ![]() таких, что
таких, что ![]() выполняется
выполняется ![]()
![]() .
.
Функция f (x)
называется убывающей (невозрастающей) на интервале (a,b), если ![]() таких, что
таких, что ![]() ,
, ![]()
![]() .
.
Теорема 1. Пусть f (x) дифференцируема на (a,b). Тогда если ![]()
![]()
![]() , то f (x)
возрастающая (убывающая) на (a,b).
, то f (x)
возрастающая (убывающая) на (a,b).
Замечание 1. Условие ![]()
![]() является необходимым и достаточным для
неубывания (невозрастания) f (x) на (a,b).
является необходимым и достаточным для
неубывания (невозрастания) f (x) на (a,b).
Интервалы возрастания и убывания функции называются интервалами монотонности.
5.2. Точки экстремума функций.
Необходимое и достаточное условия существования экстремума функции
Точка ![]() называется точкой локального максимума
(локального минимума) функции
называется точкой локального максимума
(локального минимума) функции ![]() , если
, если ![]() - проколотая окрестность т.
- проколотая окрестность т. ![]() такая что
такая что ![]()
![]()
![]() . Точки
локального максимума и локального минимума называются точками экстремума функции.
. Точки
локального максимума и локального минимума называются точками экстремума функции.
Теорема 1. (Необходимое условие экстремума). Пусть т. ![]() - точка экстремума функции
- точка экстремума функции ![]() . Тогда либо
. Тогда либо ![]() либо
либо ![]() не существует.
не существует.
Теорема 2. (Достаточное условие экстремума). Пусть ![]() непрерывна в т.
непрерывна в т. ![]() и
дифференцируема в
и
дифференцируема в ![]() . Тогда, если выполняются
следующие условия:
. Тогда, если выполняются
следующие условия:
либо а) ![]() ,
, ![]()
![]() , либо б)
, либо б) ![]()
![]() ,
, ![]() , то
, то ![]() имеет экстремум в т.
имеет экстремум в т. ![]() , а именно: локальный минимум в случае а) и
локальный максимум в случае б).
, а именно: локальный минимум в случае а) и
локальный максимум в случае б).
Пример. Найти интервалы монотонности и точки экстремума функции 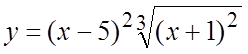 .
.
Ñ ![]() . Вычислим производную.
. Вычислим производную.
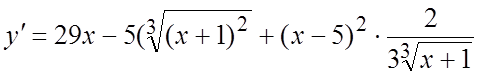 = =
= =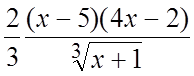 .
Экстремум может достигаться при
.
Экстремум может достигаться при ![]() ,
, 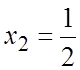 и
и ![]() , так
как эти значения принадлежат области определения
, так
как эти значения принадлежат области определения ![]() и f (-1) не существует, f
(1/2)=0, f (5)=0. Исследуем знаки первой производной
на интервалах
и f (-1) не существует, f
(1/2)=0, f (5)=0. Исследуем знаки первой производной
на интервалах ![]() ,
,
(-1, 1/2), (1/2, 5), ![]() .
.
![]()
![]()
![]()
![]()
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-1 1/2 5
Например, ![]() . По методу интервалов получаем остальные
знаки. Тогда
. По методу интервалов получаем остальные
знаки. Тогда ![]() возрастает на (-1, 1/2) и
возрастает на (-1, 1/2) и ![]() ;
; ![]() убывает
на
убывает
на ![]() и (1/2, 5). Точки
и (1/2, 5). Точки ![]() и
и
![]() - локальные минимумы, а
- локальные минимумы, а ![]() - точка локального максимума функции.#
- точка локального максимума функции.#
Пример. Найти соотношение между радиусом R и высотой H цилиндра, имеющего при данном объеме V наименьшую полную поверхность S.
ÑФормула площади полной поверхности имеет вид
![]() . Так как
. Так как ![]() , то
выразив
, то
выразив 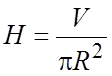 можно получить
можно получить 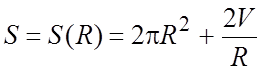 .
Исследуем S (R)
на экстремум.
.
Исследуем S (R)
на экстремум. 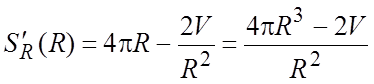 . Экстремум возможен если
. Экстремум возможен если ![]() т.е.
т.е. 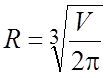 .
Проверим смену знаков
.
Проверим смену знаков ![]()
|
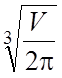 +
+
![]()
![]()
![]()
![]()
![]() 0
0
При 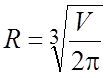 S(R) имеет локальный минимум и подставляя
S(R) имеет локальный минимум и подставляя ![]() получаем
получаем ![]() . #
. #
Пусть ![]() непрерывна на
непрерывна на ![]() и точки
и точки
![]() такие что
такие что ![]() ,
, ![]() либо равна 0, либо не
либо равна 0, либо не ![]() . Тогда наибольшее значение
. Тогда наибольшее значение ![]() на
на ![]() есть
есть 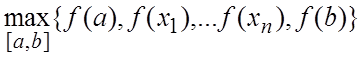 , а наименьшее -
, а наименьшее - 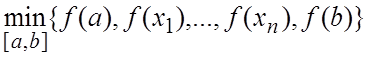 .
.
Пример. Найти наибольшее и наименьшее значения 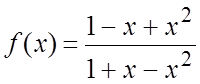 на [0, 1]. Ñ
Вычислим производную:
на [0, 1]. Ñ
Вычислим производную:
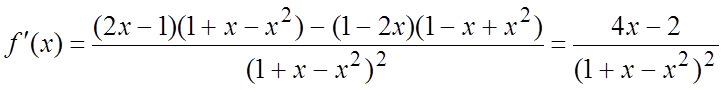 .
.
Заметим что, ![]() на [0, 1]. Экстремум возможен при
на [0, 1]. Экстремум возможен при 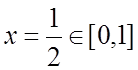 . Тогда fнаибольшее=
. Тогда fнаибольшее=![]() , fнаименьшее=
, fнаименьшее=![]() . Здесь наибольшее значение достигается в
двух точках, а наименьшее – в одной. #
. Здесь наибольшее значение достигается в
двух точках, а наименьшее – в одной. #
1.Показать, что
функция ![]() везде возрастает.
везде возрастает.
2. Показать, что
функция ![]() везде убывает.
везде убывает.
Найти интервалы монотонности функций.
3. 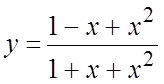 . 4.
. 4. ![]() . 5.
. 5. 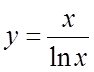 . 6.
. 6. ![]() .
.
7. 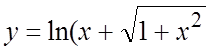 .
.
Найти экстремумы функций.
8. 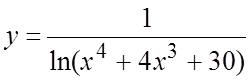 . 9.
. 9. 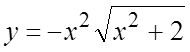 . 10.
. 10.
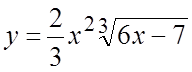 .
.
11. 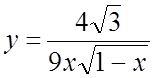 . 12.
. 12. 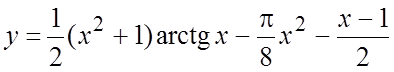 .
.
Найти наибольшее и наименьшее значения данных функций в указанных интервалах.
13. ![]() . 14.
. 14. ![]() .
.
15. ![]()
![]() . 16.
. 16. 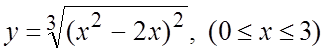 .
.
17. 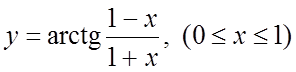 .
.
18. Периметр равнобедренного треугольника равен 2p. Каковы должны быть его стороны, чтобы объем конуса, образованного вращением этого треугольника вокруг высоты, опущенной на основание, был наибольшим.
19. Найти стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса R.
20. Бревно длиной в 20 м имеет форму усеченного конуса, диаметры оснований которого равны соответственно 2 и 1 м. Требуется вырубить из бревна балку с квадратным поперечным сечением, ось которой совпадала бы с осью бревна и объем которой был бы наибольшим. Каковы должны быть размеры балки?
21. Из трех
досок одинаковой ширины сколачивается желоб для подачи воды. При каком угле ![]() наклона боковых стенок к днищу желоба
площадь поперечного сечения желоба будет наибольшей.
наклона боковых стенок к днищу желоба
площадь поперечного сечения желоба будет наибольшей.
5.3. Исследование функций на выпуклость и вогнутость.
Точки перегиба функций.
Функция ![]() называется выпуклой (вогнутой) на
интервале (a, b),
если
называется выпуклой (вогнутой) на
интервале (a, b),
если ![]() касательная расположена выше (ниже)
графика функции.
касательная расположена выше (ниже)
графика функции.
Теорема 1. Пусть ![]() дважды дифференцируема
на (a, b),
дважды дифференцируема
на (a, b), ![]()
![]() тогда
тогда ![]() выпуклая (вогнутая) на (a, b).
выпуклая (вогнутая) на (a, b).
Точка ![]() называется точкой перегиба графика
функции, если слева от этой точки график функции выпуклый (вогнутый), а справа
– вогнутый (выпуклый).
называется точкой перегиба графика
функции, если слева от этой точки график функции выпуклый (вогнутый), а справа
– вогнутый (выпуклый).
Теорема 2 (необходимое условие перегиба). Пусть ![]() - точка перегиба графика функции
- точка перегиба графика функции ![]() . Тогда или
. Тогда или ![]() или
или ![]() не существует.
не существует.
Теорема 3 (достаточное условие перегиба). Пусть ![]() дважды дифференцируема в некоторой
окрестности т.
дважды дифференцируема в некоторой
окрестности т. ![]() и либо
и либо![]() существует
и конечна, либо
существует
и конечна, либо ![]() не существует и
не существует и ![]() меняет знак при переходе через т.
меняет знак при переходе через т. ![]() . Тогда
. Тогда ![]() - точка
перегиба графика функции.
- точка
перегиба графика функции.
Пример. Найти интервалы выпуклости, вогнутости и точки перегиба графика
функции 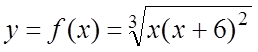 .
.
Ñ Область определения D(y)=R. Вычислим вторую производную.
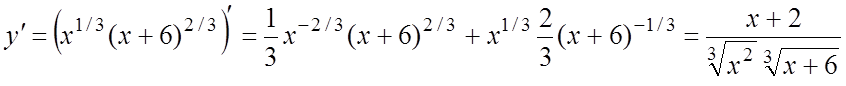 .
.
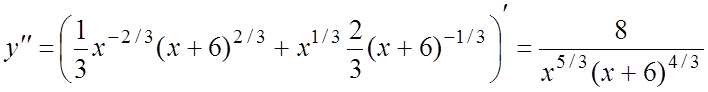 .
.
Точки возможного
перегиба :![]() , т.к.
, т.к. ![]() и
и ![]() не существует и
не существует и ![]() .
Проверим смену знака
.
Проверим смену знака ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.