Вычисление КИ-2.
Теорема 14.7. Если
линия AB задана в параметрической форме: ![]() , где
, где ![]() -
непрерывно дифференцируемые функции, и при изменении параметра t от
-
непрерывно дифференцируемые функции, и при изменении параметра t от ![]() к
к ![]() кривая описывается именно от точки A к точке B, то
кривая описывается именно от точки A к точке B, то
 (5.5)
(5.5)
причем КИ-2 существует, если существует определенный интеграл.
Следствия.
а) Для плоской линии AB: ![]() и функций
и функций ![]() ,
, ![]() :
: 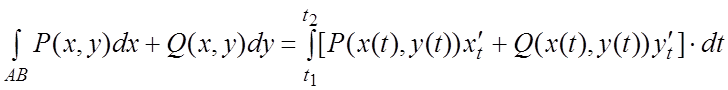 .
.
б) Для заданной явно плоской линии ![]()
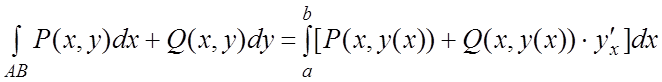 . (5.6)
. (5.6)
Независимость КИ-2 от пути интегрирования
Теорема 14.8. Если функции ![]() непрерывны
вместе со своими частными производными первого порядка в некоторой замкнутой
ограниченной поверхностно односвязной области V, то равносильны следующие четыре утверждения:
непрерывны
вместе со своими частными производными первого порядка в некоторой замкнутой
ограниченной поверхностно односвязной области V, то равносильны следующие четыре утверждения:
1) 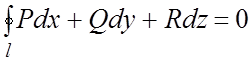 , где l – замкнутый контур, лежащий внутри V;
, где l – замкнутый контур, лежащий внутри V;
2) 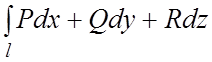 не зависит от выбора пути интегрирования;
не зависит от выбора пути интегрирования;
3) ![]() есть полный дифференциал некоторой однозначной
функции
есть полный дифференциал некоторой однозначной
функции ![]() , заданной в точках V;
, заданной в точках V;
4) выполняются равенства: 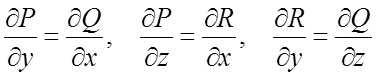 .
.
Функция ![]() может быть найдена,
например, по формуле
может быть найдена,
например, по формуле
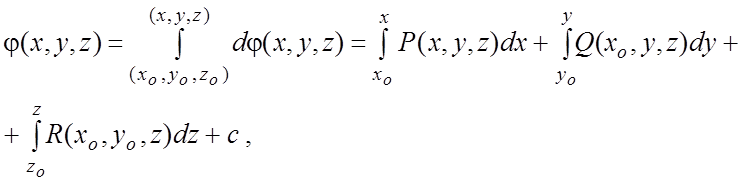 (5.7)
(5.7)
где ![]() -
некоторая фиксированная точка области V, c
– произвольная постоянная.
-
некоторая фиксированная точка области V, c
– произвольная постоянная.
Связь между КИ-1 и КИ-2. Пусть спрямляемая (не имеющая особых
точек) линия AB имеет в каждой точке касательную,
положительное направление которой составляет с осью координат углы ![]() . Тогда
. Тогда
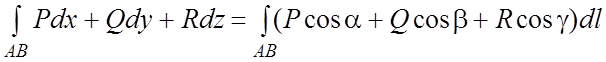 .
.
Связь КИ-2 с двойным
интегралом (формула Грина). Теорема 14.9. Пусть: 1) функции ![]() непрерывны
и имеют непрерывные частные производные в открытой односвязной области
непрерывны
и имеют непрерывные частные производные в открытой односвязной области ![]() ; 2) l– кусочно-гладкий контур, ограничивающий область
; 2) l– кусочно-гладкий контур, ограничивающий область ![]() , и при положительном обходе lближайшая часть области S находится слева от наблюдателя.
Тогда справедлива формула:
, и при положительном обходе lближайшая часть области S находится слева от наблюдателя.
Тогда справедлива формула:
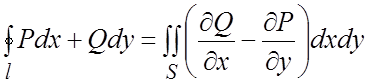 .
.
Площадь плоской области. Площадь s фигуры S, ограниченной простым кусочно-гладким контуром l, равна
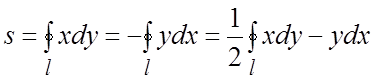 .
.
Пример 20. Вычислить КИ-2: 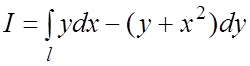 , где L – дуга параболы
, где L – дуга параболы ![]() ,
проходимая от точки
,
проходимая от точки ![]() до точки
до точки ![]() .
.
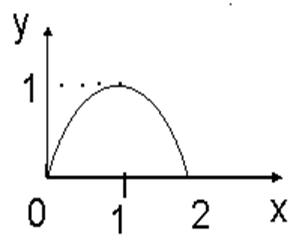 Ñ Кривая l
представлена на рис.14.24.
Ñ Кривая l
представлена на рис.14.24.
|
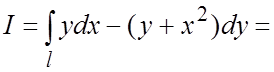 =
=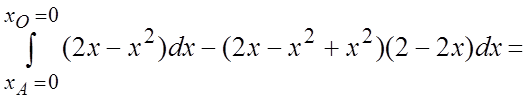 =
=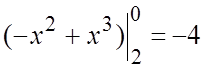 . #
. #
 Пример 21. Вычислить КИ-2:
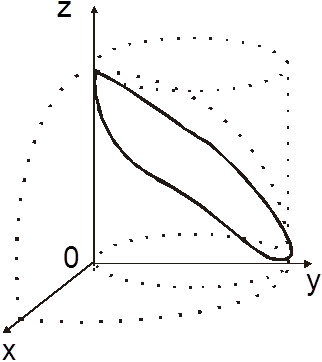
Пример 21. Вычислить КИ-2: 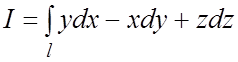 , где l – замкнутый контур, полученный пересечением сферы
, где l – замкнутый контур, полученный пересечением сферы ![]() и цилиндра
и цилиндра ![]()
![]() , обходимый против часовой стрелки, если
смотреть из начала координат (рис.14.25).
, обходимый против часовой стрелки, если
смотреть из начала координат (рис.14.25).
|
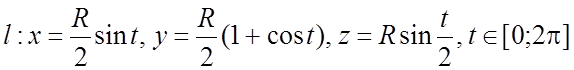 ;
; 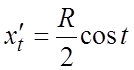 ,
, 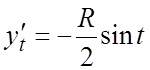 ,
, 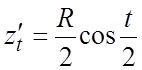 . По формуле (5.5)
. По формуле (5.5) 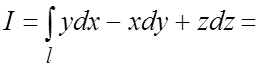 =
=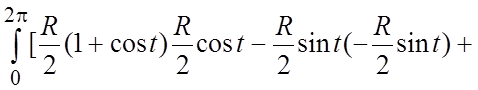
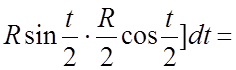
=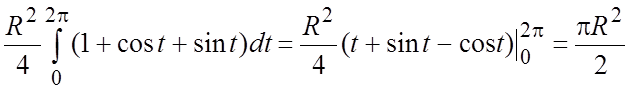 .#
.#
Пример 22. Найти первообразную функции ![]() , если
, если ![]() .
.
Ñ По формуле (5.7) при ![]() получим
получим
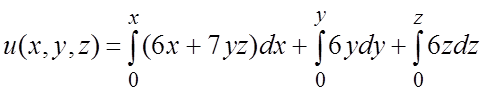
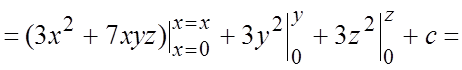
![]() .#
.#
Задачи для самостоятельного решения
Вычислить криволинейные интегралы второго рода:
97. 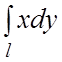 , где l – отрезок прямой
, где l – отрезок прямой ![]() от точки пересечения ее с осью Ox до точки пересечения с осью Oy.
от точки пересечения ее с осью Ox до точки пересечения с осью Oy.
98. 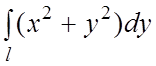 , где l – контур прямоугольника с вершинами
, где l – контур прямоугольника с вершинами ![]()
![]() , указанными в порядке обхода l.
, указанными в порядке обхода l.
99. 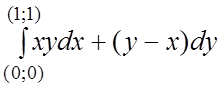 вдоль линий: 1)
вдоль линий: 1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() , 4)
, 4) ![]() .
.
100. 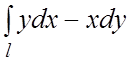 , l – эллипс
, l – эллипс ![]() , обходимый в
положительном направлении.
, обходимый в
положительном направлении.
101. 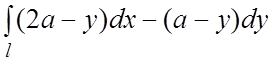 , где l – первая от начала координат арки
циклоиды
, где l – первая от начала координат арки
циклоиды ![]() ,
, ![]() .
.
102. 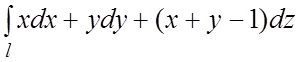 , где l – отрезок прямой от точки (1;1;1) до
точки (2;3;4).
, где l – отрезок прямой от точки (1;1;1) до
точки (2;3;4).
103. 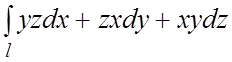 , где l – дуга винтовой линии
, где l – дуга винтовой линии ![]()
![]() .
.
104. 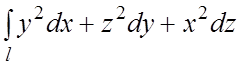 , где l – линия пересечения сферы
, где l – линия пересечения сферы ![]() и цилиндра
и цилиндра ![]() (
(![]() ) , обходимая против часовой стрелки, если
смотреть из начала координат (часть кривой Вивиани).
) , обходимая против часовой стрелки, если
смотреть из начала координат (часть кривой Вивиани).
Убедиться, что подынтегральное выражение является полным дифференциалом, и вычислить КИ-2:
105. 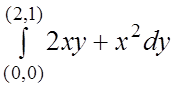 . 106.
. 106. 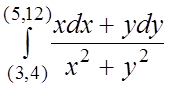 . 107.
. 107.  .
.
108. 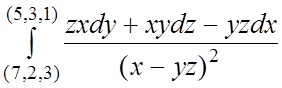 (контурное интегрирование не
пересекает поверхность
(контурное интегрирование не
пересекает поверхность ![]() .
.
Найти первообразную функцию и по полному дифференциалу:
109. ![]() .
.
110. ![]() .
.
111. 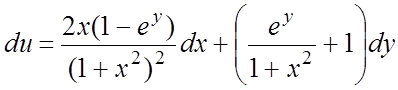 .
.
112. ![]() .
.
113. 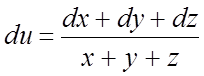 . 114.
. 114. 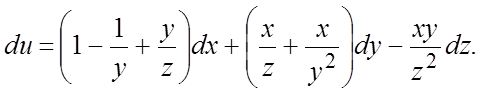
С помощью формулы Грина вычислить КИ-2:
115. 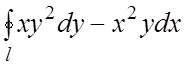 , где l – окружность
, где l – окружность ![]() .
.
116. 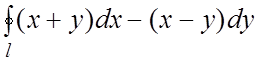 , где l – эллипс
, где l – эллипс ![]() .
.
117. Вычислить 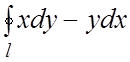 ,
где l – простой замкнутый контур,
пробегаемый в положительном направлении. Указание. Рассмотреть случаи:
1) начало координат находится вне контура l; 2) контур l окружает начало координат.
,
где l – простой замкнутый контур,
пробегаемый в положительном направлении. Указание. Рассмотреть случаи:
1) начало координат находится вне контура l; 2) контур l окружает начало координат.
118. В каждой точке эллипса ![]() приложена сила
приложена сила ![]() , равная
по величине расстоянию от точки M до
центра эллипса и направленная к центру эллипса. Найти работу
, равная
по величине расстоянию от точки M до
центра эллипса и направленная к центру эллипса. Найти работу ![]() при перемещении в положительном
направлении: а) вдоль дуги эллипса в первом октанте; б) вдоль всего эллипса.
при перемещении в положительном
направлении: а) вдоль дуги эллипса в первом октанте; б) вдоль всего эллипса.
119. Сила по величине обратно пропорциональна
расстоянию точки ее приложения от оси Oz , перпендикулярна к этой оси и направлена к ней.
Найти работу этой силы по окружности ![]() от точки
от точки ![]() до точки
до точки ![]() . Указание.
. Указание.
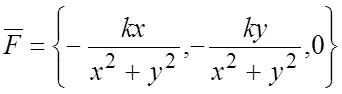 .
.
14.6. Поверхностные интегралы
14.6.1. Двусторонние поверхности и их ориентация
Гладкая поверхность s называется двусторонней поверхностью , если при возвращении в исходную точку после обхода замкнутого контура , лежащего на s и не имеющего общих точек с ее границей, направление нормали к поверхности не меняется.
Совокупность всех точек поверхности с приписанными в них по указанному правилу нормалями называется определенной стороной поверхности.
Выбор определенной стороны поверхности называется ориентацией поверхности. Выбранная сторона - это положительная сторона поверхности. Для замкнутой поверхности положительной считается внешняя сторона.
Если s задана неявным уравнением ![]() , то сторона характеризуется одним из
единичных нормальных векторов
, то сторона характеризуется одним из
единичных нормальных векторов
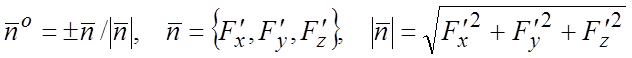 .
(6.1)
.
(6.1)
Если s задана явным уравнением ![]() ,
, ![]() , то
сторона характеризуется одним из векторов
, то
сторона характеризуется одним из векторов ![]() :
:
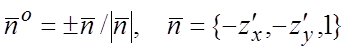 ,
, 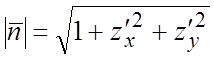 . (6.2)
. (6.2)
14.6.2. Поверхностный интеграл первого рода (ПИ-1)
Пусть : 1) в точках
двусторонней гладкой (или кусочно-гладкой) поверхности s из пространства ![]() , ограниченной кусочно-гладким контуром,
определена ограниченная скалярная функция
, ограниченной кусочно-гладким контуром,
определена ограниченная скалярная функция ![]() ; 2)
; 2) ![]() - произвольное разбиение s на n частей
- произвольное разбиение s на n частей ![]() с площадями
с площадями ![]() и диаметрами
и диаметрами ![]() ; 3)
; 3)![]()
![]() - произвольный набор точек;
- произвольный набор точек;
4)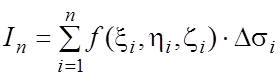 - интегральная сумма, соответствующая данному разбиению
поверхности s и выбору точек
- интегральная сумма, соответствующая данному разбиению
поверхности s и выбору точек
![]() .
.
Определение. Конечный предел интегральной суммы ![]() при
при ![]()
![]() ,не зависящий ни от способа разбиения
поверхности s, ни от выбора
точек
,не зависящий ни от способа разбиения
поверхности s, ни от выбора
точек ![]() , называется поверхностным интегралом
первого рода от функции
, называется поверхностным интегралом
первого рода от функции ![]() по поверхности s:
по поверхности s:
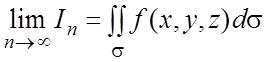 .
.
Вычисление ПИ-1.
Теорема 14.10. Если
: 1) поверхность s
задана неявным уравнением ![]() и
и ![]() есть решение этого уравнения при
есть решение этого уравнения при ![]() или
или ![]() -
решение уравнения при
-
решение уравнения при ![]() , или
, или ![]() -решение
уравнения при
-решение
уравнения при ![]() , где
, где ![]() -
проекции s на плоскости
-
проекции s на плоскости ![]() - соответственно, 2) между точками s и ее соответствующей проекцией
установлено взаимно однозначное соответствие, то
- соответственно, 2) между точками s и ее соответствующей проекцией
установлено взаимно однозначное соответствие, то
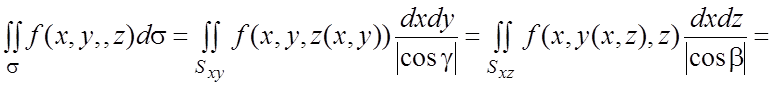
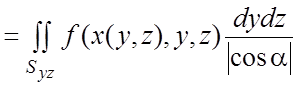 ,
(6.3)
,
(6.3)
причем ПИ-1 существует, если существуют соответствующие двойные интегралы.
Здесь ![]() координаты
вектора
координаты
вектора ![]() и находятся по формулам (6.1).
и находятся по формулам (6.1).
ПИ-1 не зависит от выбора стороны поверхности.
Следствие. При явном задании s : ![]() в силу (6.2) из (6.3) получим
в силу (6.2) из (6.3) получим
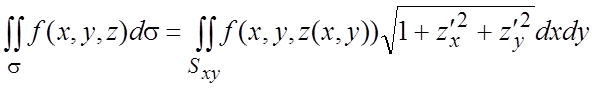 . (6.4)
. (6.4)
Некоторые приложения ПИ-1
1. Масса материальной поверхности. Пусть ![]() - поверхностная
плотность материальной поверхности s площади s.
Тогда масса этой поверхности
- поверхностная
плотность материальной поверхности s площади s.
Тогда масса этой поверхности
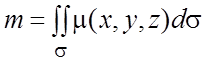 .
.
2. Площадь искривленной поверхности s . Если принять в предыдущей формуле ![]() ,
то масса поверхности s
числено равна площади s
, т.е.
,
то масса поверхности s
числено равна площади s
, т.е.
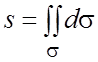 .
.
3. Статические моменты материальной
поверхности s с поверхностной плотностью ![]() и массой m относительно плоскостей
и массой m относительно плоскостей ![]() соответственно равны:
соответственно равны: 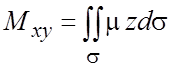 ,
, 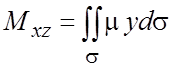 ,
, 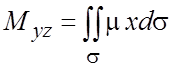 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.